AAS和ASA的Sine定律
章节大纲
-
A triangle has two angles that measure 60 ∘ and 45 ∘ . The length of the side between these two angles is 10. What are the lengths of the other two sides?
::三角形有两个角度, 测量 60 和 45 。 这两个角度之间的边长度是 10 。 另外两边的长度是 多少 ?Law of Sines
::Sines法律Consider the non right triangle below. We can construct an altitude from any one of the vertices to divide the triangle into two right triangles as show below.
::考虑下方的非右三角形。 我们可以从任何一个顶端构造一个高度, 将三角形分为两个右三角形, 如下所示 。from the diagram we can write two trigonometric functions involving h :
::从图表中我们可以写出两个三角函数,涉及 h:sin C = h b a n d sin B = h c b sin C = h c sin B = h
::C=hbandsinB=hcbsinC=h csinB=h 罪行=hbandsinB=hbsinC=h csinB=hSince both are equal to h , we can set them equal to each other to get:
::由于两者均等于h,我们可以把它们等同起来,以便:b sin C = c sin B and finally divide both sides by b c to create the proportion:
::bsinC=csinB,最后将两边除以 bc 以得出比例 :sin C c = sin B b
::Cc=sinBb 罪、cc=sinBbIf we construct the altitude from a different vertex, say B , we would get the proportion: sin A a = sin C c . Now, the transitive property allows us to conclude that sin A a = sin B b . We can put them all together as the Law of Sines: sin A a = sin B b = sin C c . In the problems that follow, we will use the Law of Sines to solve triangles.
::如果我们从不同的顶端构造高度, 比如 B, 我们就会得到比例: sinAa=sinCc。 现在, 过渡性财产让我们可以得出结论, sinAa=sinBb。 我们可以把它们合在一起, 成为Sines定律: sinAa=sinB=sinC。 在接下来的问题中, 我们将使用Sines定律来解决三角形 。Let's solve the following triangles using the Law of Sines.
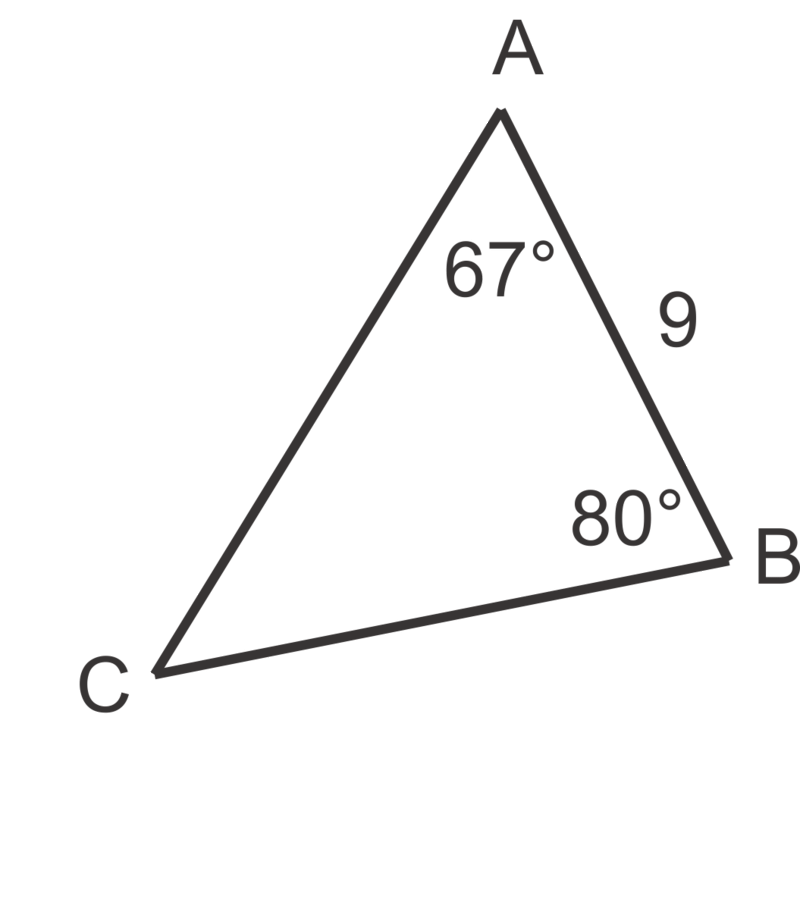
::让我们用辛尼定律来解决以下三角形。Since we are given two of the three angles in the triangle, we can find the third angle using the fact that the three angles must add up to 180 ∘ . So, m ∠ A = 180 ∘ − 45 ∘ − 70 ∘ = 650 ∘ . Now we can substitute the known values into the Law of Sines proportion as shown:
::既然三角形的三个角度中有两个, 我们就可以找到第三个角度, 使用三个角度必须加到 180 。 所以, mA= 180 45 70 650 。 现在我们可以将已知的值 替换成 Sines 法则比例 :sin 65 ∘ a = sin 70 ∘ 15 = sin 45 ∘ c
::15=45=45=c 时间轴: 时间轴: @ 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴: 时间轴:Taking two ratios at a time we can solve the proportions to find a and c using cross multiplication.
::在一个我们可以用乘法来解答比例时 取两个比例 来找到一个和c 乘法乘法To find a :
::查找 :sin 65 ∘ a = sin 70 ∘ 15 a = 15 sin 65 ∘ sin 70 ∘ ≈ 14.5
::15a=15sin65sin7014.5To find c :
::查找 c:sin 70 ∘ 15 = sin 45 ∘ c c = 15 sin 45 ∘ sin 70 ∘ ≈ 11.3
::15=sin45 cc=15sin45 sin70 11.3This particular triangle is an example in which we are given two angles and the non-included side or AAS (also SAA).
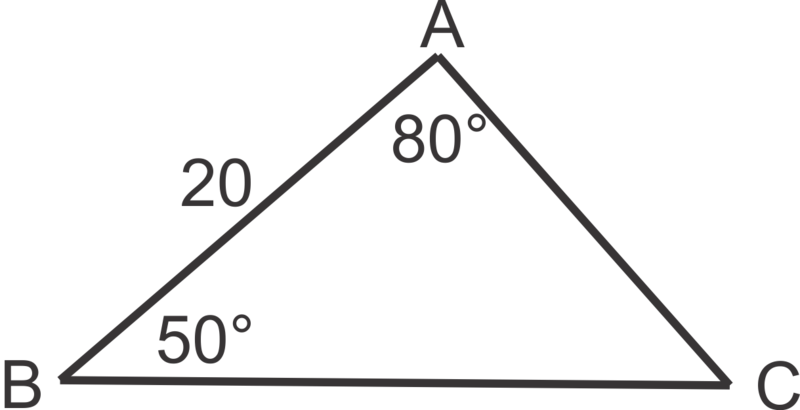
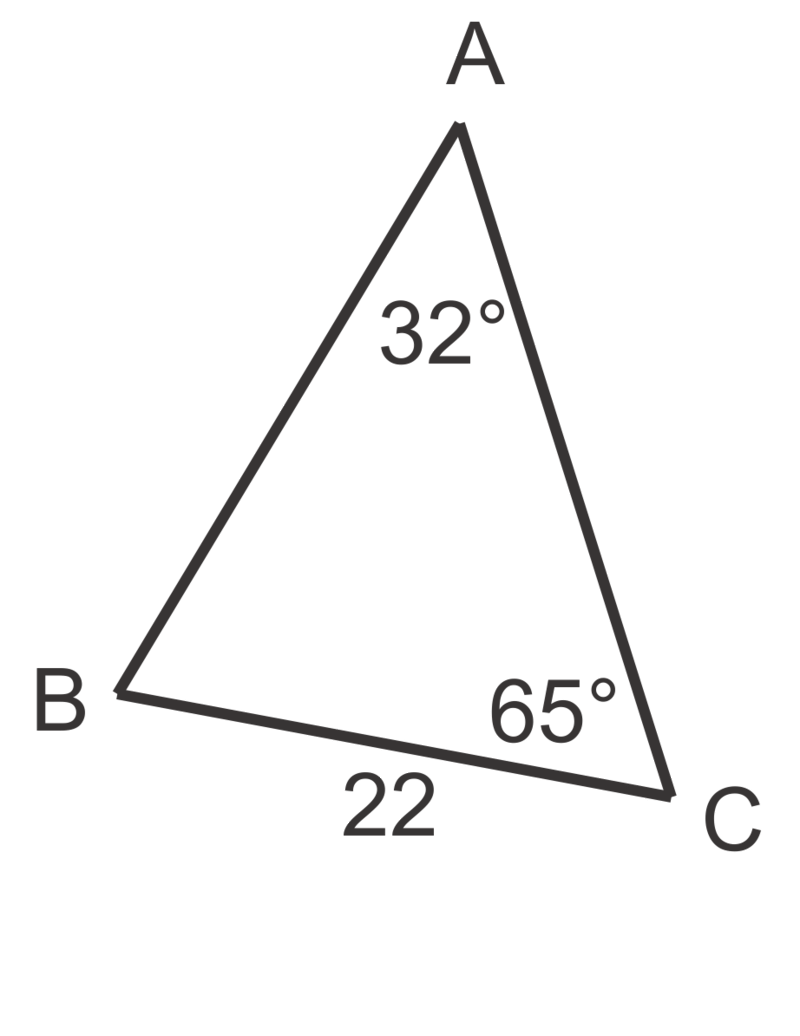
::这个特定的三角形就是一个例子,我们从两个角度和未包括的侧面或AAS(也指SAA)得到的。In this problem we are given two angles and a side as well but the side is between the angles. We refer to this arrangement as ASA. In practice, in doesn’t really matter whether we are given AAS or ASA. We will follow the same procedure as #1 above. First, find the third angle: m ∠ A = 180 ∘ − 50 ∘ − 80 ∘ = 50 ∘ .
::在此问题上,我们被赋予了两个角度和一个侧面,但侧面是角度之间的。 我们称这种安排为 ASA 。 实际上, 无论是AAS还是 ASA 都无关紧要 。 我们将遵循上面#1 的相同程序 。 首先, 找到第三个角度 : mA = 180 50 80 50 。Second, write out the appropriate proportions to solve for the unknown sides, a and b .
::第二,写出解决未知方的适当比例,a和b。To find a :
::查找 :sin 80 ∘ a = sin 50 ∘ 20 a = 20 sin 80 ∘ sin 50 ∘ ≈ 25.7
::20a=20sin80_sin50_25.7To find b :
::查找 b:sin 50 ∘ b = sin 50 ∘ 20 b = 20 sin 50 ∘ sin 50 ∘ = 20
::20b=20sin50=20sin50=50sin50=20Notice that c = b and m ∠ C = m ∠ B . This illustrates a property of isosceles triangles that states that the base angles (the angles opposite the congruent sides) are also congruent.
::注意 c=b 和 mC=mB 。 这显示了一等分三角形的属性, 该三角形表示基角( 对齐边的角) 也是一致的 。Now, let's solve the following problem.
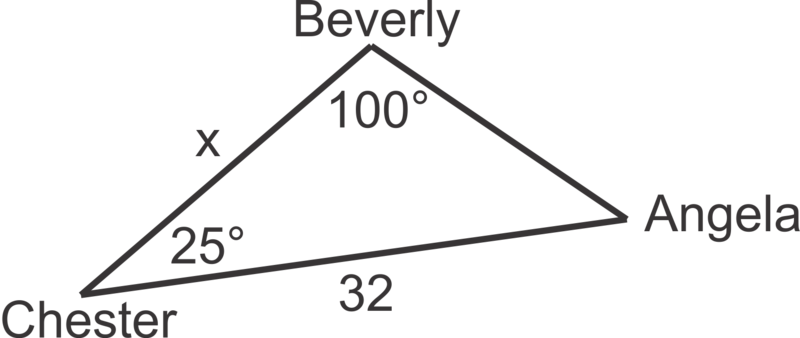
::现在,让我们解决下面的问题。Three fishing ships in a fleet are out on the ocean. The Chester is 32 km from the Angela. An officer on the Chester measures the angle between the Angela and the Beverly to be 25 ∘ . An officer on the Beverly measures the angle between the Angela and the Chester to be 100 ∘ . How far apart, to the nearest kilometer are the Chester and the Beverly?
::一艘船队中的三艘渔船在海上。切斯特号距离安吉拉32公里。切斯特号的一位官员将安吉拉号与贝弗利号之间的角度测量为25英尺。贝弗利号的一位官员将安吉拉号与切斯特号之间的角度测量为100英尺。切斯特号和贝弗利号离最近的公里有多远?First, draw a picture. Keep in mind that when we say that an officer on one of the ships is measuring an angle, the angle she is measuring is at the vertex where her ship is located.
::首先,绘制一张图片。记住,当我们说某艘船上的军官正在测量一个角度时, 她测量的角度是她船只所在的顶峰。Now that we have a picture, we can determine the angle at the Angela and then use the Law of Sines to find the distance between the Beverly and the Chester.
::现在我们有了一张图片, 我们可以确定安吉拉的角 然后用辛那斯定律 找到贝弗利和切斯特之间的距离。The angle at the Angela is 180 ∘ − 100 ∘ − 25 ∘ = 55 ∘ .
::安吉拉的角是1801002555。Now find x ,
::现在找到 x,sin 55 ∘ x = sin 100 ∘ 32 x = 32 sin 55 ∘ sin 100 ∘ ≈ 27
::-============================================================================================================================================ ================================================================================================================================================================================================================================================================================================================================================================================The Beverly and the Chester are about 27 km apart.
::贝弗利和切斯特相距约27公里Examples
::实例Example 1
::例1Earlier, you were asked to find the lengths of the other two sides of a triangle that has two angles that measure 60 ∘ and 45 ∘ and a side between these two angles with length 10.
::早些时候,有人要求你找到三角形其他两侧的长度。 三角形的两边有两个角度, 测量60++和45++++和两个角度之间的一个边, 长度为10。The measure of the triangle's third angle is 180 ∘ − 60 ∘ − 45 ∘ = 75 ∘
::三角形第三个角的度量为 180604575sin 45 ∘ x = sin 75 ∘ 10 , so x = 10 sin 45 ∘ sin 75 ∘ ≈ 7.29 sin 60 ∘ y = sin 75 ∘ 10 , so y = 10 sin 60 ∘ sin 75 ∘ ≈ 8.93
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}所以 x=10sin45\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}7.29sin60\7\29sin60\7}y=sin75\10 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}所以y=10sin60\sin75\8.93 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}Example 2
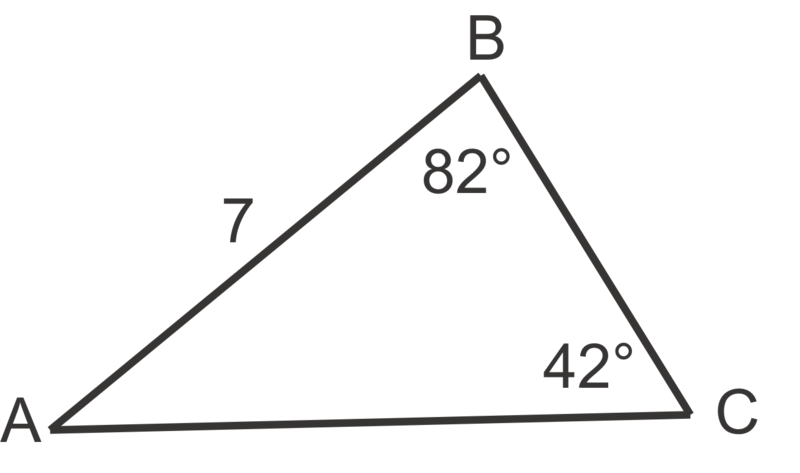
::例2Solve the following triangle.
::解决以下三角形。m ∠ A = 180 ∘ − 82 ∘ − 24 ∘ = 74 ∘
::=========================================================================================================================================== =================================================================================================================================================================================================================================================================================================================================================================================sin 24 ∘ b = sin 74 ∘ 11 , so b = 11 sin 24 ∘ sin 74 ∘ ≈ 4.7 sin 82 ∘ c = sin 74 ∘ 11 , so c = 11 sin 82 ∘ sin 74 ∘ ≈ 11.3
::=11sin24\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Example 3
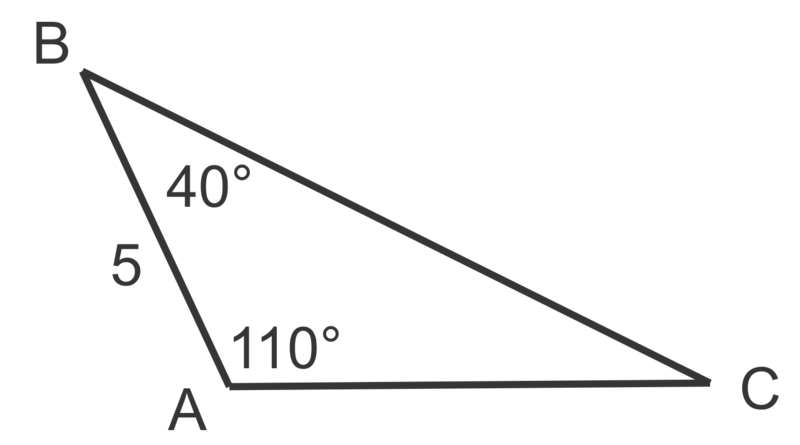
::例3Solve the following triangle.
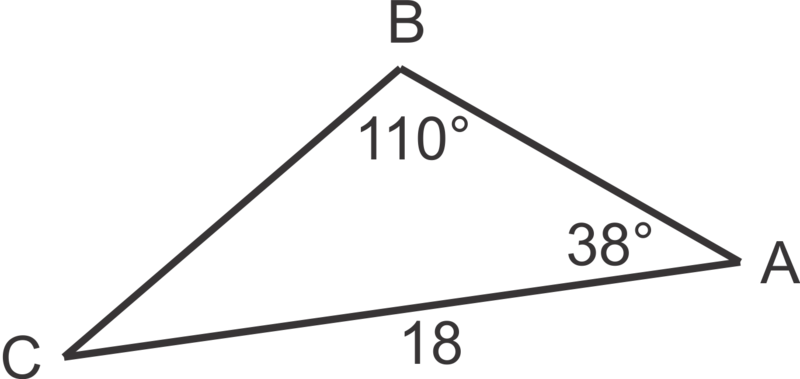
::解决以下三角形。m ∠ C = 180 ∘ − 110 ∘ − 38 ∘ = 32 ∘
::==================================================================================sin 38 ∘ a = sin 110 ∘ 18 , so a = 18 sin 38 ∘ sin 110 ∘ ≈ 11.8 sin 32 ∘ c = sin 110 ∘ 18 , so c = 18 sin 32 ∘ sin 110 ∘ ≈ 10.2
::c=18sin3211011010.2。Example 4
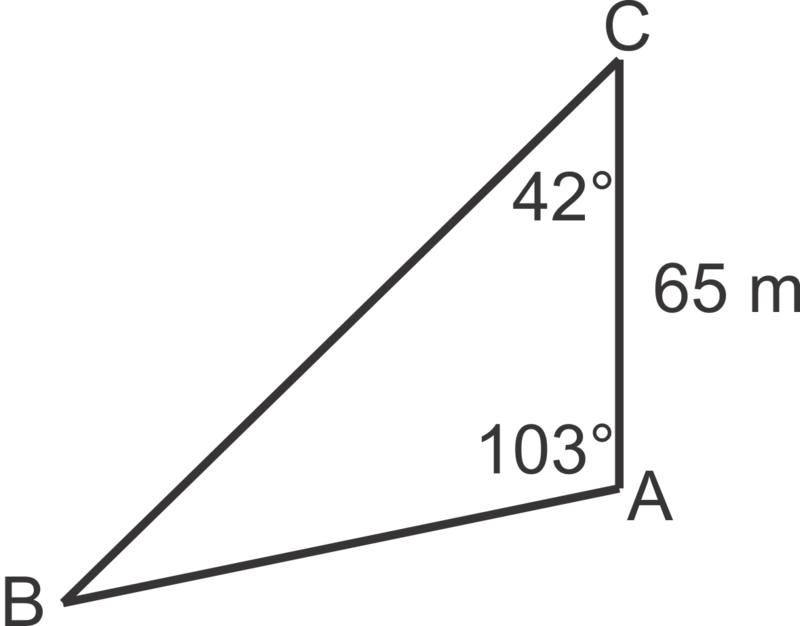
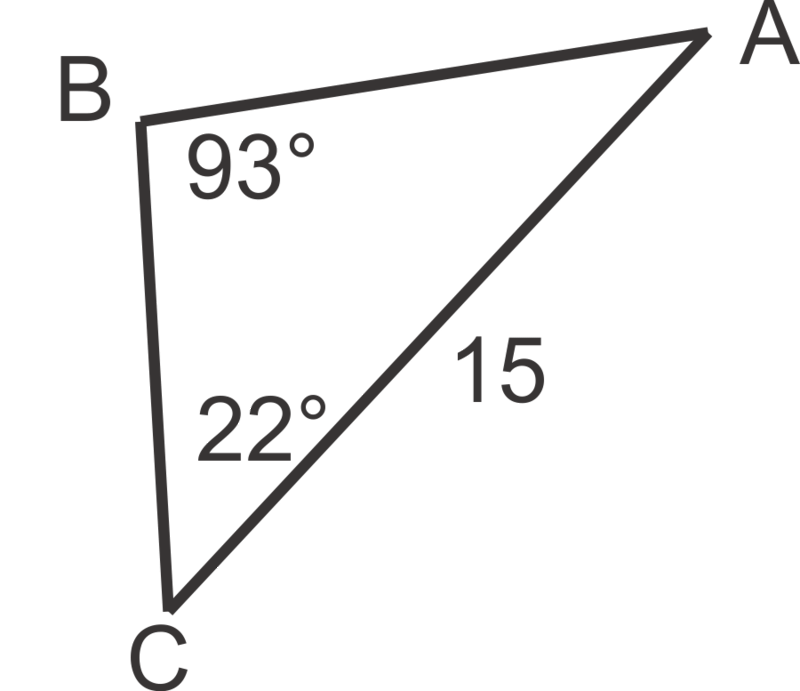
::例4A surveying team is measuring the distance between point A on one side of a river and point B on the far side of the river. One surveyor is positioned at point A and the second surveyor is positioned at point C , 65 m up the riverbank from point A . The surveyor at point A measures the angle between points B and C to be 103 ∘ . The surveyor at point C measures the angle between points A and B to be 42 ∘ . Find the distance between points A and B .
::测量组正在测量河流一侧的A点和河另一边的B点之间的距离,一位测量员部署在A点,而第二位测量员位于C点,距离A点的河岸上65米处。A点测量员测量B点和C点之间的角为103。C点测量员测量A点和B点之间的角为42。查找A点和B点之间的距离。m ∠ B = 180 ∘ − 103 ∘ − 42 ∘ = 35 ∘ sin 35 ∘ 65 = sin 42 ∘ c c = 65 sin 42 ∘ sin 35 ∘ ≈ 75.8 m
::mB=180103423535356542cc=65423575.8米Review
::回顾Solve the triangles. Round your answers to the nearest tenth.
::解开三角形。 将答案绕到最近的十分之一 。Using the given information, solve Δ A B C .
::使用给定的信息解析 {ABC} 。- .
-
-
m
∠
A
=
85
∘
m
∠
C
=
40
∘
a
=
12
-
m
∠
A
=
85
∘
m
∠
C
=
40
∘
a
=
12
- .
-
-
m
∠
B
=
60
∘
m
∠
C
=
25
∘
a
=
28
-
m
∠
B
=
60
∘
m
∠
C
=
25
∘
a
=
28
- .
-
-
m
∠
B
=
42
∘
m
∠
A
=
36
∘
b
=
8
-
m
∠
B
=
42
∘
m
∠
A
=
36
∘
b
=
8
- .
-
-
m
∠
B
=
30
∘
m
∠
A
=
125
∘
c
=
45
-
m
∠
B
=
30
∘
m
∠
A
=
125
∘
c
=
45
Use the Law of Sines to solve the following world problems.
::利用辛那法来解决以下的世界问题。-
A surveyor is trying to find the distance across a ravine. He measures the angle between a spot on the far side of the ravine,
X
, and a spot 200 ft away on his side of the ravine,
Y
, to be
100
∘
. He then walks to
Y
the angle between
X
and his previous location to be
20
∘
. How wide is the ravine?
::勘测器试图找到峡谷的距离。 他测量了峡谷的远方的X和Y两侧200英尺以外的200英尺之间的角。 然后他走到Y, X和他先前的位置之间的角是20英寸。 峡谷宽度是多少? -
A triangular plot of land has angles
46
∘
and
58
∘
. The side opposite the
46
∘
angle is 35 m long. How much fencing, to the nearest half meter, is required to enclose the entire plot of land?
::三角形地块有角度46°和角度58°。46°和角度58°的对面角为35米长。需要多少栅栏才能覆盖整块土地?
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -