Section: 椭圆的方形 | 6.1 椭圆的等量

Section outline

Ken is having a disagreement with his friend Scott. Scott says that the track that they run on at school is not really an ellipse, but an oval. Ken thinks that is a silly distinction, since ovals and are the same thing. Who is correct?
::肯和他的朋友斯科特有分歧。斯科特说,他们在学校运行的轨道其实不是一个椭圆,而是一个奥瓦尔。肯认为这是愚蠢的区别,因为奥瓦尔是同一回事。谁是正确的?

Equation of an Ellipse
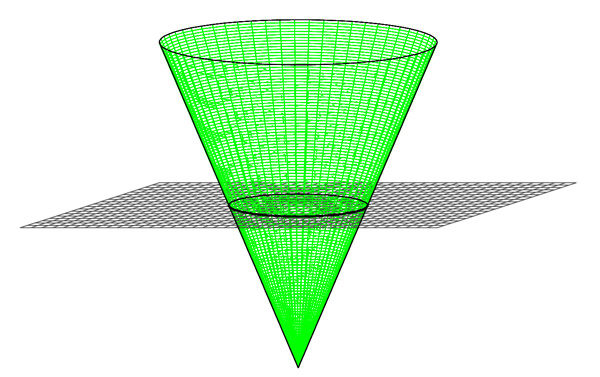
::椭圆的方形

When a plane "slices through" one side of a cone, we get either a circle or an “oval-shaped” object as shown below. It turns out that this is no ordinary oval, but something called an ellipse , a shape with special properties.
::当一个平面“切片通过”锥形的一面时,我们会得到一个圆形或“卵形”物体,如下文所示。结果显示,这不是普通的oval,而是一种叫做椭圆的形状,一种具有特殊属性的形状。

a. Cone "sliced through" by a plane 90 ^o to the axis of the cone to form a *circle* .		b. Cone "sliced through" by a plane at an angle to form an *ellipse* .

Ellipses can be defined by some of their properties. One way to define an ellipse is as a “stretched out circle”. It’s the shape you would get if you sketched a circle on a deflated balloon and then stretched out the balloon evenly in two opposite directions:
::椭圆可以根据其某些属性来定义。给椭圆下定义的一种方法是“伸展的圆 ” 。如果在淡化的气球上绘制圆形图,然后将气球平均地向两个相反的方向伸展,它就会形成形状:

It’s also the shape of the surface of water that results when you tilt a round glass:
::当你倾斜一个圆玻璃时,它也是水面的形状:

Or an ellipse could be thought of as the shape of a circle drawn on a piece of paper when it is viewed at an angle.
::或椭圆可被视为圆形的形状,当从一个角度看待时,它会画在一张纸上。

Equations of Ellipses
::椭圆平

This “stretching” can be represented algebraically. For simplicity, take the circle of radius 1 centered at the origin (0,0). The distance formula tells us that this is the set of points $\begin{aligned} (x, y) \end{aligned}$ that is a distance 1 unit away from the origin.
::此“ 伸展” 可以代表代数。简单来说, 以圆半径 1 以原点为中心( 0, 0) 。距离公式告诉我们这是一组点( x, y) , 就是远离原点的距离 1 单位。

\begin{aligned} D & = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}} \\ 1 & = \sqrt{(x - 0)^{2} + (y - 0)^{2}} \\ 1 & = x^{2} + y^{2} \end{aligned}

::D=(x1-x2)2+(y1-y2)21=(x-0)2+(y-0)2+(y-0)21=x2+y2

This equation, $\begin{aligned} x^{2} + y^{2} = 1 \end{aligned}$ , can be altered to stretch the circle in the horizontal (i.e. $\begin{aligned} x - \end{aligned}$ axis) direction by dividing the $\begin{aligned} x \end{aligned}$ variable by a constant $\begin{aligned} a > 1 \end{aligned}$ ,
::此方程式 x2+y2=1 可以通过将 x 变量除以常数 a>1 来修改以拉展水平( 即 x- 轴) 方向的圆形。

\begin{aligned} {(\frac{x}{a})}^{2} + y^{2} = 1 \end{aligned}

xx)2+y2=1

Why does this stretch the circle horizontally? Well, the effect of dividing $\begin{aligned} x \end{aligned}$ by $\begin{aligned} a \end{aligned}$ is that for each $\begin{aligned} y - \end{aligned}$ value in an ordered pair $\begin{aligned} (x, y) \end{aligned}$ that satisfies the original equation, the corresponding $\begin{aligned} x \end{aligned}$ value must be multiplied by $\begin{aligned} a \end{aligned}$ in order for the pair to make a solution to the altered equation. So solutions $\begin{aligned} (x, y) \end{aligned}$ of the circle are in one-to-one correspondence with solutions $\begin{aligned} (a x, y) \end{aligned}$ of the altered equation, hence stretching the corresponding graph to the left and right by a factor of $\begin{aligned} a \end{aligned}$ .
::为何横跨圆形 ? 那么, 将 x 除以 a 的效果是, 对于符合原始方程的一对定序( x,y) 中的每个 y- 值, 对应的 x 值必须乘以 a 方程式才能使对等方程式的变换方程式得到解决方案。因此圆形的解决方案( x,y) 是在一对一对一对应变方程式的解决方案( 轴,y) , 从而将对应的图表向左和右拉展到一个系数。

Here is the graph of $\begin{aligned} {(\frac{x}{2})}^{2} + y^{2} = 1 \end{aligned}$ :
::这里是 (x2) 2+y2= 1 的图形 :

Generalizing the equation by allowing a stretch in the vertical direction, we get the following.

\begin{aligned} {(\frac{x}{a})}^{2} + {(\frac{y}{b})}^{2} = 1 \end{aligned}

::通过允许垂直方向的伸展宽度, 将方程概括化, 我们得到以下结果。 (xa) 2+( yb) 2=1

The factor $\begin{aligned} a \end{aligned}$ stretches the circle in the horizontal direction and the factor $\begin{aligned} b \end{aligned}$ stretches the circle in the vertical direction. If $\begin{aligned} a = b \end{aligned}$ , this is just a circle. When $\begin{aligned} a \neq b \end{aligned}$ , this equation represents an ellipse. The ellipse is stretched in the horizontal direction if $\begin{aligned} b < a \end{aligned}$ and it is stretched in the vertical direction if $\begin{aligned} a < b \end{aligned}$ .
::a 系数拉长水平方向的圆,b 系数拉长垂直方向的圆。如果 a=b,这只是一个圆。当 ab 时,此方程式代表椭圆。如果 b<a] ,则在水平方向伸展椭圆,如果 <b] 则在垂直方向伸展。

Often the above equation is written as follows.

\begin{aligned} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{aligned}

::上述方程式通常写成如下。 x2a2+y2b2=1

This is called the standard form of the equation of an ellipse, assuming that the ellipse is centered at (0,0).
::这称为椭圆方程的标准形式,假定椭圆以 0,0为中心。

To sketch a graph of an ellipse with the equation $\begin{aligned} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{aligned}$ , start by plotting the four axes intercepts, which are easy to find by plugging in 0 for $\begin{aligned} x \end{aligned}$ and then for $\begin{aligned} y \end{aligned}$ . Then sketch the ellipse freehand, or with a graphing program or calculator.
::要绘制方程式 x2a2+y2b2=1 的椭圆形图,先绘制四个轴拦截图,这些截图很容易找到,先插入 0 ,然后插入 x,然后插入y。然后绘制椭圆自由手图,或者用图形程序或计算器绘制。

The Foci
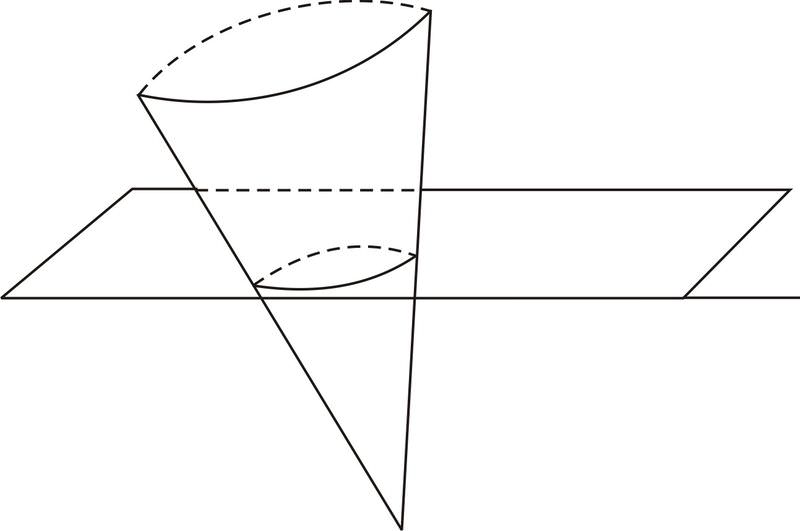
::爱爱爱爱友

In every ellipse there are two special points called the foci (foci is plural, focus is singular), which lie inside the ellipse and which can be used to define the shape. For an ellipse centered at (0,0) that is wider than it is tall, its major axis is horizontal and its foci are at $\begin{aligned} (\sqrt{a^{2} - b^{2}}, 0) \end{aligned}$ and $\begin{aligned} (- \sqrt{a^{2} - b^{2}}, 0) \end{aligned}$ .
::在每一个椭圆中,都有两个特殊点叫做 foci( 集合是多元的, 焦点是单数的) , 它们位于椭圆内, 可以用来定义形状。对于位于( 0,0) 的、大于其高的椭圆, 其主轴是水平的, 其顶部是( a2 - b2,0) 和 (-a2 - b2,0) 。

What is the significance of these points? Ellipses relate to these points much as a circle relates to its center . Remember a circle can be thought of as the set of points in a plane that are a certain distance from the center point, in fact, that is typically the definition of a circle. Well, the foci act like the center except that there are two of them. An ellipse is the set of points where the sum of the distance between each point on the ellipse and each of the two foci is a constant number. In the diagram below, for any point $\begin{aligned} P \end{aligned}$ on the ellipse, $\begin{aligned} F_{1} P + F_{2} P = d \end{aligned}$ , where $\begin{aligned} F_{1} \end{aligned}$ and $\begin{aligned} F_{2} \end{aligned}$ are the foci and $\begin{aligned} d \end{aligned}$ is a constant.
::这些点的意义是什么 ? 椭圆与这些点有关, 因为圆与圆的中心有关。记住一个圆可以被看成是与圆的中心点有一定距离的平面上的一组点。事实上, 这通常是圆的定义。那么, foci 的动作就像中间点, 除了其中两个点以外。椭圆是一系列点的组合, 其中椭圆和两个面的每个点之间的距离总和是一个恒定数。在下面的图表中, 对于椭圆上的 P 点, F1P+F2P=d, F1 和 F2 是一个常数。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about Ken and Scott's disagreement.
::之前有人问你肯和斯科特的分歧

Scott is correct. Ovals are not the same as ellipses.
::Scott是对的 Ovals和省略号不一样

Example 2
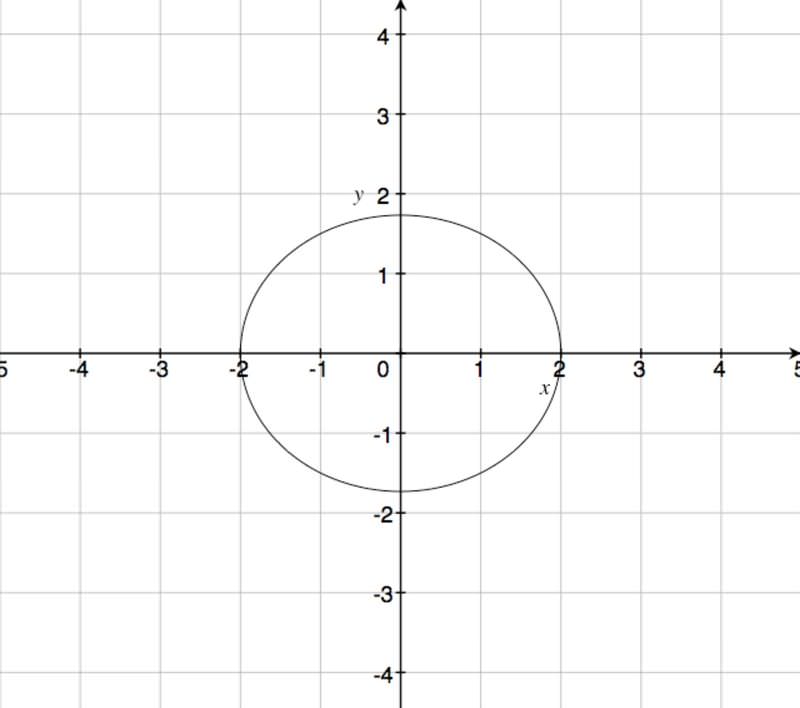
::例2

Sketch the graph of $\begin{aligned} \frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 \end{aligned}$ .
::绘制 x24+y29=1 的图形。

This equation can be rewritten as $\begin{aligned} \frac{x^{2}}{2^{2}} + \frac{y^{2}}{3^{2}} = 1 \end{aligned}$ .
::此方程式可以重写为 x222+Y232=1 。

To sketch, we set $\begin{aligned} x = 0 \end{aligned}$ and solve for $\begin{aligned} y \end{aligned}$ to find the x-intercepts and set $\begin{aligned} y = 0 \end{aligned}$ and solve for $\begin{aligned} x \end{aligned}$ to find the $\begin{aligned} y - \end{aligned}$ intercepts.
::对于草图,我们设置 x=0 并解决 y 查找 x 界面,设置 y =0 和解决 x 查找 y - 拦截。

The four points we get are (0,3), (0,-3), (2,0), and (-2,0).
::我们得到的四点是(0,3)、(0,3)、(2,0)和(2.0)。

Plot those points and sketch the ellipse:
::绘制这些点并绘制椭圆草图:

Example 3
::例3

Sketch the graph of $\begin{aligned} \frac{x^{2}}{16} + y^{2} = 1 \end{aligned}$ .
::绘制 x216+y2=1 的图形。

This can be rewritten as $\begin{aligned} \frac{x^{2}}{4^{2}} + \frac{y^{2}}{1^{2}} = 1 \end{aligned}$ . After finding the intercepts and sketching the graph with the same process as above, we have:
::这可以改写为 x242+y212=1. 查找拦截和用上述相同程序绘制图表草图后,我们有:

The segment spanning the long direction of the ellipse is called the major axis , and the segment spanning the short direction of the ellipse is called the minor axis . So in the last example the major axis is the segment from (-4,0) to (4,0) and the minor axis is the segment from (0,-1) to (0,1).
::椭圆的长方向段称为主轴,椭圆的短方向段称为小轴。在最后一个例子中,主要轴是从(4,0)到(4,0)的段,小轴是从(0,1)到(0,1)的段。

The major and minor axes are examples of what are sometimes called reference lines . Apollonius, the Ancient Greek mathematician who wrote an early treatise on conics, used these and other reference lines to orient . Though the Greeks did not use a coordinate plane to discuss geometry, these reference lines offer a framing perspective that is similar to the Cartesian plane that we use today. Apollonius’ way of framing conics with reference lines was the closest mathematics came to the system of coordinate geometry that you know so well until Descartes’ and Fermat’s systematic work in the seventeenth century.
::主要轴和次要轴是有时被称为参考线的例子。古希腊数学家阿波罗尼乌斯(Apolonius)早期撰写了有关二次曲线的论文,他用这些和其他参考线来指导东方。尽管希腊人没有使用协调平面来讨论几何学,但这些参考线提供了一个与我们今天使用的笛卡尔平面相似的框架视角。阿波罗尼乌斯用参考线构建二次曲线的方式是最接近的数学进入了协调几何系统,而你非常清楚这一点,直到迪卡特斯和费马特在17世纪的系统工作。

Example 4
::例4

What is the full range of the eccentricity of an ellipse? What does it look like near the extremes of this range?
::椭圆的偏心性究竟是什么?

Foci can be used to measure how far an ellipse is “stretched” from a circle. The symbol $\begin{aligned} ε \end{aligned}$ stands for the eccentricity of an ellipse, and it is defined by the distance between the foci divided by the length of the major axis, or $\begin{aligned} \frac{\sqrt{a^{2} - b^{2}}}{a} \end{aligned}$ for horizontally oriented ellipses and $\begin{aligned} \frac{\sqrt{b^{2} - a^{2}}}{b} \end{aligned}$ for vertically oriented ellipses. Since a circle is an ellipse where $\begin{aligned} a = b \end{aligned}$ , circles have an eccentricity of 0.
::焦距可以用来测量椭圆“ 伸展” 从圆的“ 伸展” 。符号表示椭圆的偏心性, 其定义是按主轴长度除以方形之间的距离, 或按水平方向的椭圆的 a2 - b2a 和垂直方向的椭圆的 b2 - a2b。由于圆是一个以 a=b 的椭圆, 圆的偏心性为 0 。

The interval of possible values is $\begin{aligned} ε \in [0, 1) \end{aligned}$ . At $\begin{aligned} ε = 0 \end{aligned}$ , the ellipse is a circle; as the eccentricity approaches 1 it becomes more and more elongated.
::可能的值间隔为 [0,1] 。在 0 时, 椭圆是一个圆圈; 当偏心接近 1 时, 椭圆会越来越长。

Example 5
::例5

Not all equations for ellipses start off in the standard form above. For example, $\begin{aligned} 25 x^{2} + 9 y^{2} = 225 \end{aligned}$ is an ellipse. Put it in the proper form and graph it.
::并非所有的椭圆方程式都以上述标准格式启动。例如, 25x2+9y2=225is a extlipse。将其以正确的形式显示并绘制图表。

To graph $\begin{aligned} 25 x^{2} + 9 y^{2} = 225 \end{aligned}$ as an ellipse:
::图25x2+9y2=225作为椭圆:

$\begin{aligned} \frac{x^{2}}{9} + \frac{y^{2}}{25} = 1 \end{aligned}$ ..... First, divide both sides by 225
::x29+y225=1...。首先,将两边除以 225

$\begin{aligned} \frac{x^{2}}{3^{2}} + \frac{y^{2}}{5^{2}} = 1 \end{aligned}$ ..... Find the intercepts
::x232+y252=1.... 查找拦截

Graphing, we have:
::图表,我们有:

Example 6
::例6

It was mentioned above that when a round glass of water is tilted, the surface of the water is an ellipse. Using our working definition of an ellipse as “stretched out circle”, explain why you think the water takes this shape.
::上面提到,当一圆杯水倾斜时,水的表面是椭圆。用我们对椭圆的工作定义“伸展圆形 ” , 解释为什么你认为水会形成这种形状。

Answers may vary, but should explain why the shape that results stretches a circle in one direction because the width of the glass is constant.
::答案可能各有不同,但应解释为什么结果的形状将圆向一个方向拉长,因为玻璃的宽度是恒定的。

Example 7
::例7

Try to sketch this ellipse where the numbers don’t turn out to be so neat: $\begin{aligned} 3 x^{2} + 4 y^{2} = 12 \end{aligned}$ .
::试着画出数字不那么整洁的椭圆: 3x2+4y2=12。

To graph $\begin{aligned} 3 x^{2} + 4 y^{2} = 12 \end{aligned}$ :
::图3x2+4y2=12:

$\begin{aligned} \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1 \end{aligned}$ ..... First, divide both sides by 12
::x24+y23=1...。首先,将两边除以 12

$\begin{aligned} \frac{x^{2}}{2^{2}} + \frac{y^{2}}{{\sqrt{3}}^{2}} = 1 \end{aligned}$ ..... Find the intercepts
::x222+Y232=1....

Graphing, we get:
::绘图,我们得到:

Review
::回顾

Convert each equation to the standard form of an ellipse.
::将每个方程转换为椭圆的标准形式。

$\begin{aligned} x^{2} + 4 y^{2} = 4 \end{aligned}$
::x2+4y2=4

$\begin{aligned} 9 x^{2} + 16 y^{2} = 144 \end{aligned}$
::9x2+16y2=144

$\begin{aligned} 25 x^{2} + 36 y^{2} = 900 \end{aligned}$
::25x2+36y2=900

$\begin{aligned} 36 x^{2} + 9 y^{2} = 324 \end{aligned}$
::36x2+9y2=324

$\begin{aligned} 49 x^{2} + y^{2} = 49 \end{aligned}$
::49x2+y2=49

$\begin{aligned} 16 x^{2} + 4 y^{2} = 64 \end{aligned}$
::16x2+4y2=64

$\begin{aligned} x^{2} + 2 y^{2} = 2 \end{aligned}$
::x2+2y2=2

$\begin{aligned} 3 x^{2} + 4 y^{2} = 12 \end{aligned}$
::3x2+4y2=12

$\begin{aligned} 5 x^{2} + 6 y^{2} = 30 \end{aligned}$
::5x2+6y2=30

$\begin{aligned} 6 x^{2} + 3 y^{2} = 18 \end{aligned}$
::6x2+3y2=18

$\begin{aligned} 7 x^{2} + y^{2} = 7 \end{aligned}$
::7x2+y2=7

$\begin{aligned} 4 x^{2} + 2 y^{2} = 8 \end{aligned}$
::4x2+2y2=8

Graph the following ellipses.
::绘制下方的省略号图。

$\begin{aligned} 9 x^{2} + 16 y^{2} = 144 \end{aligned}$
::9x2+16y2=144

$\begin{aligned} 49 x^{2} + y^{2} = 49 \end{aligned}$
::49x2+y2=49

$\begin{aligned} x^{2} + 2 y^{2} = 2 \end{aligned}$
::x2+2y2=2

$\begin{aligned} 7 x^{2} + y^{2} = 7 \end{aligned}$
::7x2+y2=7

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Equation of an Ellipse ::椭圆的方形

Equations of Ellipses ::椭圆平

The Foci ::爱 爱 爱 爱 友

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)