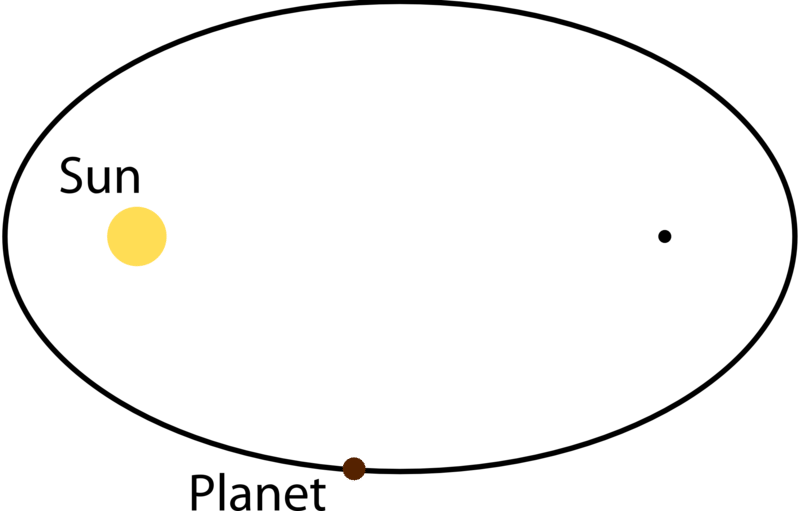节: Ellips 的焦点属性 | 6.2 椭圆的焦点财产

章节大纲

In 1602, the astronomer Johannes Kepler was working on a problem for his boss Tycho Brahe. He was continuing a centuries-old study trying to devise a formula that could calculate the orbits of the planets, specifically Mars in this case. He worked for years on the problem with the most advanced technology of the time, but was never satisfied with the results as they were never truly accurate or reliable.
::1602年,天文学家约翰尼斯·开普勒(Johannes Kepler)为他的上司Brahe(Tycho Brahe)研究了一个问题。他正在继续一项长达数百年的研究,试图设计出一个计算行星轨道的公式,特别是火星。他多年来一直致力于研究当时最先进的技术问题,但从未对结果感到满意,因为这些结果从来不是真正准确或可靠的。

To simplify his calculations, he hit upon the concept that a planet sweeps out equal areas of space (in a pie-slice shaped figure with the sun at the tip) in equal amounts of time, despite differences in the distance of the planet from the sun.
::为了简化他的计算,他抓住了这样一个概念,即一个行星在相等的时间里(在以太阳为顶端的披萨形像为圆形的图象中)将相等的空间面积扫出,尽管地球与太阳的距离不同。

For the next three years he attempted to design the perfect equation to describe an orbit which would fit this and other observations he was using.
::在接下来的三年里,他试图设计一个完美的方程式,描述一个适合这一轨道和他正在使用的其他观测结果的轨道。

Finally, in 1605, he realized that he had the answer. His realization/discovery would firmly place him as one of the most famous scientists of all time.
::最后,在1605年,他意识到自己有答案。他的觉悟/发现将牢牢地将他定位为有史以来最著名的科学家之一。

What did he realize?
::他意识到什么了?

Focal Property of Ellipses
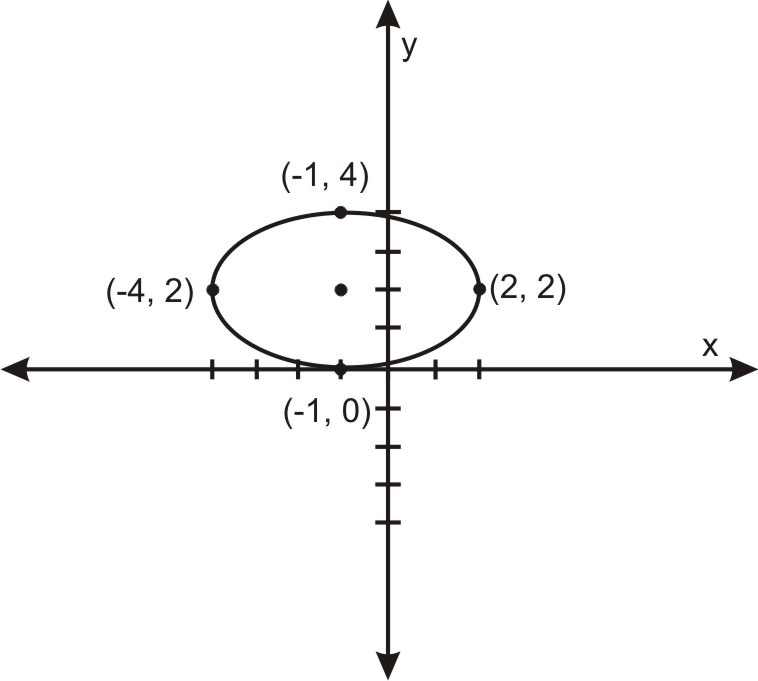
::Ellips 的焦点属性

Ellipses Not Centered at the Origin
::不居于起源点的椭圆

To find an equation for centered around another point, say $\begin{aligned} (h, k) \end{aligned}$ , simply replace $\begin{aligned} x \end{aligned}$ with $\begin{aligned} x - h \end{aligned}$ and $\begin{aligned} y \end{aligned}$ with $\begin{aligned} y - k \end{aligned}$ . This will shift all the points of the ellipse to the right $\begin{aligned} h \end{aligned}$ units (or left if $\begin{aligned} h < 0 \end{aligned}$ ) and to up $\begin{aligned} k \end{aligned}$ units (or down if $\begin{aligned} k < 0 \end{aligned}$ ). So the general form for a horizontally- or vertically-oriented ellipse is:
::要找到围绕其它点的方程式, 例如 (h, k) , 只需将 x 替换为 x- h 和 y 替换为 y- k 。这将将椭圆的所有点移到右边的 h 单位( 或如果 h < 0) 和上方的 k 单位( 如果 k < 0) , 或下方的 k 单位( 如果 k < 0) 。因此水平或垂直方向的椭圆的一般形式是 :

$\begin{aligned} \frac{(x - h)^{2}}{a^{2}} + \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$

:x-h)2a2+(y-k)2b2=1

It is centered about the point $\begin{aligned} (h, k) \end{aligned}$ . If $\begin{aligned} b < a \end{aligned}$ , the ellipse is horizontally oriented and has foci $\begin{aligned} (h + \sqrt{a^{2} - b^{2}}, k) \end{aligned}$ and $\begin{aligned} (h - \sqrt{a^{2} - b^{2}}, k) \end{aligned}$ on its horizontal major axis. If $\begin{aligned} a < b \end{aligned}$ , it is vertically oriented and has foci $\begin{aligned} (h, k + \sqrt{a^{2} - b^{2}}) \end{aligned}$ and $\begin{aligned} (h, k - \sqrt{a^{2} - b^{2}}) \end{aligned}$ on its vertical major axis.
::它围绕点 (h,k) 。 b<a) , 椭圆是水平方向的, 在其水平主轴上具有 foci (h+a2-b2,k) 和 (h-a2-b2,k) 。如果 a <b) , 它则垂直方向, 并且在其垂直主轴上具有 foci (h, k+a2-b2) 和 (h, k-a2-b2) 。

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about the problem that astronomer Johannes Kepler was working on for his boss, Tycho Brahe.
::之前有人问过你天文学家约翰尼斯·开普勒为他的上司泰乔·布拉赫工作的问题

Kepler's realization was that, even though he had deliberately avoided them for a very long time because they were so simple, ellipses were the perfect shape to make all of his calculations come together.
::开普勒意识到,尽管他故意避免它们很长一段时间因为它们是如此简单, 省略号是完美的形状使得他所有的计算都汇合在一起。

When a planet orbits the sun (or when any object orbits any other), it takes an elliptical path and the sun lies at one of the two foci of the ellipse. Kepler's laws regarding planetary motion are accurate enough to produce modern computations which are still used to predict the motion of artificial satellites today.
::当一个行星在太阳轨道上运行(或者当任何物体在其他轨道上运行)时,它走的是椭圆路径,太阳位于椭圆的两端之一。开普勒关于行星运动的法律非常准确,足以产生现代计算方法,如今仍然用来预测人造卫星的运动。

Example 2
::例2

Explain why subtracting $\begin{aligned} h \end{aligned}$ from the $\begin{aligned} x - \end{aligned}$ term and $\begin{aligned} k \end{aligned}$ from the $\begin{aligned} y - \end{aligned}$ term in the equation for an ellipse shifts the ellipse $\begin{aligned} h \end{aligned}$ horizontally and $\begin{aligned} k \end{aligned}$ vertically.
::解释为何从椭圆方程式的x-term和 y-term 中减去 h和 k, 将椭圆水平和 k 垂直移动。

If $\begin{aligned} (x, y) \end{aligned}$ is a solution to $\begin{aligned} \frac{(x - h)^{2}}{a^{2}} + \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$
::如果 (x,y) 是 (x-h) 2a2+(y-k) 2b2=1的解决方案

then $\begin{aligned} (x + h, y + k) \end{aligned}$ is a solution to $\begin{aligned} \frac{(x - h)^{2}}{a^{2}} + \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$
:x+h,y+k) 是 (x-h) 2a2+(y-k) 2b2=1的解决方案

This produces a graph that is shifted horizontally by $\begin{aligned} h \end{aligned}$ and vertically by $\begin{aligned} k \end{aligned}$ .
::这将生成一个以 h 水平水平移动和以 k 垂直移动的图形。

Example 3
::例3

Graph the equation $\begin{aligned} 4 x^{2} + 8 x + 9 y^{2} - 36 y + 4 = 0 \end{aligned}$ .
::方程图 4x2+8x+9y2 - 36y+4=0。

We need to get the equation into the form of general equation above. The first step is to group all the $\begin{aligned} x \end{aligned}$ terms and $\begin{aligned} y \end{aligned}$ terms, factor our the leading coefficients of $\begin{aligned} x^{2} \end{aligned}$ and $\begin{aligned} y^{2} \end{aligned}$ , and move the constants to the other side of the equation:
::我们需要将等式变成上面的一般等式形式。第一步是将所有 x 条件和 y 条件组合起来, 将我们主要的 x2 和 y2 系数乘以, 并将常数移动到等式的另一面 :

$\begin{aligned} 4 (x^{2} + 2 x) + 9 (y^{2} - 4 y) = - 4 \end{aligned}$

::4 (x2+2x)+9(y2- 4y) @%4

Now, we “complete the square” by adding the appropriate terms to the $\begin{aligned} x \end{aligned}$ expressions and the $\begin{aligned} y \end{aligned}$ expressions to make a perfect square.
::现在,我们“完成广场”,在 x 表达式和 y 表达式中添加适当的术语, 以构建一个完美的正方形。

$\begin{aligned} 4 (x^{2} + 2 x + 1) + 9 (y^{2} - 4 y + 4) = - 4 + 4 + 36 \end{aligned}$

::4 (x2+2x+1)+9(y2- 4y+4)+4+4+4+4+4+36

Now we factor and divide by the coefficients to get:
::现在,我们根据系数来考虑和划分,然后得出:

$\begin{aligned} \frac{(x + 1)^{2}}{9} + \frac{(y - 2)^{2}}{4} = 1 \end{aligned}$

:x+1)29+(y-2)24=1

And there we have it. Once it’s in this form, we see this is an ellipse is centered around the point (-1,2), it has a horizontal major axis of length 3 and a vertical minor axis of length 2, and from this we can make a sketch of the ellipse:
::在那里,我们有了它。一旦它以这种形式出现, 我们可以看到这是个椭圆, 围绕点( 1, 2), 它有一个水平主轴, 长度为3, 垂直小轴, 长度为2, 从这个角度我们可以绘制一个椭圆的草图:

Example 4
::例4

The National Statuary Hall in the United States Capital Building is an example of an ellipse-shaped room, sometimes called an “echo room”, which provide an interesting application to a property of ellipses. If a person whispers very quietly at one of the foci, the sound echoes in a way such that a person at the other focus can often hear them very clearly. Rumor has it that John Quincy Adams took advantage of this property to eavesdrop on conversations in this room.
::在美国首都大厦的国家统计厅就是一座椭圆形房间的例子,有时称为“echo室”,它为椭圆形财产提供了有趣的应用,如果一个人在一块地段悄悄地低声说话,声音回响的方式使另一个地段的人常常能非常清楚地听到它们。传言说John Quincy Adams利用这个地段窃听了这个房间里的谈话。

How do Echo Rooms work? What does the elliptical shape of the room have to do with it?
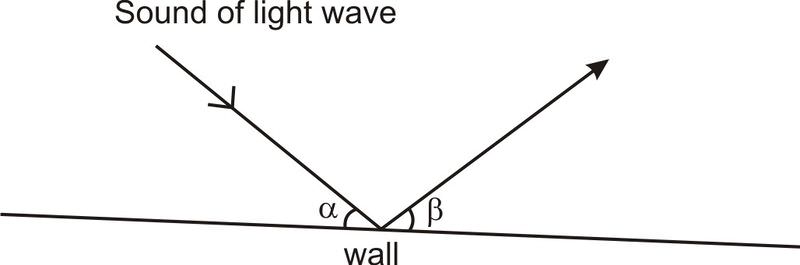
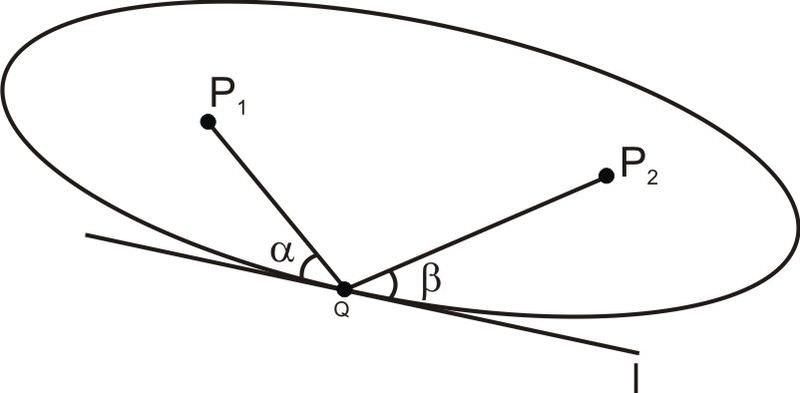
::"回声室"是怎么运作的?

The property of ellipses that makes echo rooms work is called the “optical property.” So why echoes, if this is an optical property? Well, light rays and sound waves bounce around in similar ways. In particular, they both bounce off walls at equal angles. In the diagram below, $\begin{aligned} α = β \end{aligned}$ .
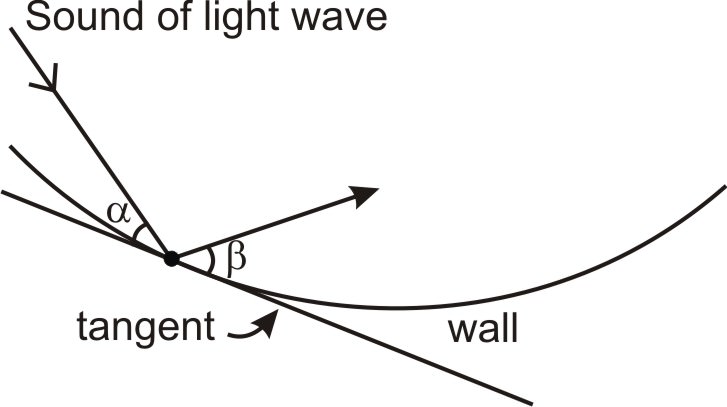
::使回声室起作用的省略号属性被称为“光属性 ” 。那么,为什么回声,如果这是光属性呢? 那么,光线和声波以类似的方式在周围反弹。特别是,它们都以平等的角度从墙上反弹。在下图中, 。

For a curved wall, they bounce at equal angles to the tangent line at that point:
::对于弯曲的墙壁,它们弹射时与正切线的角相等:

So the “optical property” of ellipses is that lines between a point on the ellipse and the two foci form equal angles to the tangent at that point, or in other words, whispers coming from one foci bounce directly to the other foci. In the diagram below, for each $\begin{aligned} Q \end{aligned}$ on the ellipse, $\begin{aligned} ∠ α ≅ ∠ β \end{aligned}$ .
::省略号的“光属性”是椭圆上的一个点与那个点对正切值的两个方形角度之间的线条,或者换句话说,从一个方形直接跳到另一个方形的耳语。在下面的图表中,对椭圆上的每个Q, 。

Example 5
::例5

Though planets take an elliptical path around the sun, these ellipses often have a very low eccentricity, meaning they are close to being circles. The diagram above exaggerates the elliptical shape of a planet’s orbit. The Earth’s orbit has an eccentricity of 0.0167. Its minimum distance from the sun is 146 million km. What is its maximum distance from the sun? If the sun’s diameter is 1.4 million kilometers, do both foci of the Earth’s orbit lie within the sun?
::虽然行星环绕太阳走离外线路径,但这些椭圆往往具有非常低的偏心性,这意味着它们接近圆环。上面的图表夸大了行星轨道的椭圆形状。地球轨道偏心性为0.0167。其与太阳的最小距离是1.46亿公里。它与太阳的最大距离是1.46亿公里。如果太阳直径为140万公里,那么地球轨道的两个角是否都在太阳之内?

Recall that the eccentricity of an ellipse is $\begin{aligned} ε = \frac{\sqrt{a^{2} - b^{2}}}{a} \end{aligned}$ .
::回顾椭圆的偏心是a2-b2a。

Assume that the orbit of the sun is an ellipse centered at (0,0). Then we can use the distance from the origin to the focus $\begin{aligned} \sqrt{a^{2} - b^{2}} \end{aligned}$ to set up the equations $\begin{aligned} 146 + 146 + 2 \sqrt{a^{2} - b^{2}} = 2 a \end{aligned}$ and $\begin{aligned} 0.167 = \frac{\sqrt{a^{2} - b^{2}}}{a} \end{aligned}$ . Solving we get $\begin{aligned} a = 175.270, b = 175.245 \end{aligned}$ , and the distance from (0,0) to the foci, $\begin{aligned} c = 2.927 \end{aligned}$ (all units are in millions of km). Finally the maximum distance from the earth to the sun is approximately 152 million km. From Kepler’s law, we know one of the foci of its orbit is at the center of the sun. The other foci is $\begin{aligned} 2 (2.927) = 5.854 \end{aligned}$ million kilometers away, so it is outside the sun (but not by very far!)
::假设太阳的轨道是一个以 0,0 为中心的椭圆轨道。然后我们可以利用起源到焦点a2-b2的距离来设置146+146+146+2a2-b2=2a和0.167=a2-2a和0.167=a2-b2a等方程。溶解我们得到的是一个=175.270,b=175.245,以及从0.0到福西的距离,c=2. 927(所有单位都以百万公里为单位)。最后,从地球到太阳的最大距离大约为1.52亿公里。根据开普勒的法律,我们知道其轨道的方形之一位于太阳的中心。其它方形为2, 2.927=5854万公里, 因此它位于太阳外( 但不是非常远 ) !

Example 6
::例6

What is the sum of the distances to the foci of the points on a vertically-oriented ellipse?
::在垂直方向的椭圆上,距离点的方形之间的距离是多少?

$\begin{aligned} 2 b \end{aligned}$
::2b 2b

Example 7
::例7

Try to graph the ellipse: $\begin{aligned} 3 x^{2} - 12 x + 5 y^{2} + 10 y - 3 = 0 \end{aligned}$ . What goes wrong?
::尝试绘制椭圆图: 3x2- 12x+5y2+10y- 3=0。出什么问题了 ?

After completing the square, we have the sum of positive numbers equaling a negative number. This is an impossibility, so the equation has no solutions.
::完成广场后,我们得到正数和负数,等于负数。这是不可能的,所以方程式没有解决办法。

Example 8
::例8

Graph the ellipse (plot points): $\begin{aligned} 5 x^{2} - 15 x - 2 y^{2} + 8 y - 50 = 0 \end{aligned}$ . What is different here? Explain what you think the graph of this equation might look like.
::绘制椭圆( 绘图点) : 5x2- 15x- 2y2+8y- 50=0。这里有什么不同 ? 请解释您认为这个方程式的图形看起来像什么。

After completing the square, the $\begin{aligned} x \end{aligned}$ term and the $\begin{aligned} y \end{aligned}$ term are opposite signs. If you plot some points you will see that the graph has two disconnected sections. This class of will be discussed in the lesson on .
::完成方块后, x 术语和 y 术语是相反的符号。如果您绘制了一些点, 您可以看到图形有两个断开的部分。此类将在课程中讨论。

Review
::回顾

Graph the following more advanced ellipses.
::如下图所示为更先进的省略号。

$\begin{aligned} (x)^{2} + \frac{(y + 2)^{2}}{9} = 1 \end{aligned}$
:x)2+(y+2)29=1

$\begin{aligned} \frac{(x + 2)^{2}}{4} + (y + 2)^{2} = 1 \end{aligned}$
:x+2)24+(y+2)2=1

%5E2%20%3D%201"> $\begin{aligned} \frac{(x + 2)^{2}}{9} + (y)^{2} = 1 \end{aligned}$
:x+2)29+2=1

$\begin{aligned} \frac{(x - 1)^{2}}{9} + \frac{(y - 4)^{2}}{16} = 1 \end{aligned}$
:x-1)29+(y-4)216=1

%5E2%20%3D%2036"> $\begin{aligned} 4 (x - 1)^{2} + 9 (y)^{2} = 36 \end{aligned}$
::4 (x- 1)2+92=36

$\begin{aligned} (x + 1)^{2} + \frac{(y - 1)^{2}}{9} = 1 \end{aligned}$
:x+1)2+(y-1)29=1

$\begin{aligned} (x - 4)^{2} + \frac{(y + 3)^{2}}{16} = 1 \end{aligned}$
:x-4)2+(y+3)216=1

%5E2%7D%7B9%7D%20%3D%201"> $\begin{aligned} \frac{(x)^{2}}{16} + \frac{(y)^{2}}{9} = 1 \end{aligned}$
:x) 216+29=1

$\begin{aligned} 4 (x + 1)^{2} + (y - 3)^{2} = 16 \end{aligned}$
::4 (x+1)2+(y-3)2=16

$\begin{aligned} (x + 4)^{2} + \frac{(y - 1)^{2}}{16} = 1 \end{aligned}$
:x+4)2+(y-1)216=1

Graph the following special-case ellipses.
::如下图所示为特例省略号。

$\begin{aligned} (x + 4)^{2} + (y + 2)^{2} = 4 \end{aligned}$
:x+4)2+(y+2)2=4

%5E2%20%3D%2016"> $\begin{aligned} (x + 2)^{2} + (y)^{2} = 16 \end{aligned}$
:x+2)2+2=16

$\begin{aligned} (x - 3)^{2} + (y - 2)^{2} = 1 \end{aligned}$
:x-3)2+(y-2)2=1

$\begin{aligned} (x + 2)^{2} + (y - 1)^{2} = 9 \end{aligned}$
:x+2)2+(y-1)2=9

$\begin{aligned} (x - 3)^{2} + (y - 1)^{2} = 9 \end{aligned}$
:x-3)2+(y-1)2=9

What do these ellipses have in common?
::这些椭圆有什么共同点?

Answer the following word problems.
::回答以下字词问题。

While the elliptical paths of planets are ellipses that are closely approximated by circles, comets and asteroids often have orbits that are ellipses with very high eccentricity. Halley’s comet has an eccentricity of 0.967, and comes within 54.6 million miles of the sun at its closest point, or “perihelion”. What is the furthest point it reaches from the sun?
::虽然行星的椭圆路径是环形接近的椭圆,但彗星和小行星的轨道往往具有极高偏心的椭圆轨道。哈雷的彗星偏心度为0.967,距离太阳最近处5 460万英里,或“近处 ” ( Periheilion ) , 距离太阳最远的地方是哪里?

Calculate the area of an ellipse with the equation $\begin{aligned} \frac{(x - h)^{2}}{a^{2}} + \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$ (Hint: use a geometric argument starting with the area of a circle.)
::用方程 (x-h) 2a2+(y-k) 2b2=1 计算椭圆的区域(提示:从圆区域开始使用几何参数)。

Design the largest possible echo room with the following constraints: You would like to spy on someone who will be 3 m from the tip of the ellipse. The room cannot be more than 100 m wide in any direction. How far from the person you’re spying on will you be standing?
::设计最大可能的回声室,有以下限制:您想监视离椭圆顶3米的人。房间在任何方向都不可能超过100米宽。您站在离您监视的人有多远?

No matter what the orientation of a stick, if you trace out the path that the shadow of the tip makes on a flat surface, you will find it is an ellipse. Describe why this is true.
::无论棍子的方向如何,如果你在平坦的表面找到尖子的阴影所创造的路径, 你会发现它是椭圆形。描述为什么这是真实的。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

Focal Property of Ellipses ::Ellips 的焦点属性

Ellipses Not Centered at the Origin ::不居于起源点的椭圆

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Focal Property of Ellipses
::Ellips 的焦点属性

Ellipses Not Centered at the Origin
::不居于起源点的椭圆

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Example 8
::例8

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源