Section: Parabolas和距离公式 | 6.3 Parabolas和距离公式

Section outline

In previous lessons on , we discussed both the circle and the ellipse, which each result from "slicing" a cone clear through from left to right. In this lesson, we will discuss the shape formed when we slice through only one side of the cone, creating a bowl-shaped figure called a parabola .
::在先前的教训中,我们讨论了圆圈和椭圆,每个圆圈都是从左到右“切开”一个圆锥。在这个教训中,我们将讨论我们切开锥体的一面时形成的形状,形成一个碗形的图象,称为抛物线。

Consider the "hourglass" figure we used in the definitions of the circle and ellipse, created by connecting two infinite cones at their tips. What limitation would there be on the angle of the slice we would take out of one of the cones, if we wanted to only get a parabola (not get an ellipse, and not hit the other cone in any way)?
::考虑一下我们在圆圈和椭圆的定义中使用的“沙漏”图,这是通过连接两颗无穷的锥子在尖尖上产生的。如果我们只想要一个抛物线(而不是获得椭圆,而不是以任何方式击中另一个锥子),那么我们从其中一颗锥子中取出的切片角度会有什么限制呢?

Parabolas and the Distance Formula
::Parabolas和距离公式

We’ve examined and circles, the two cases when a plane intersects only one side of the cone and creates a finite cross-section. Is it possible for a plane to intersect only one side of the cone, but create an infinite cross-section?
::我们研究并环绕了两种情况:一平面只交叉锥体的一面,形成一个有限的交叉剖面。一平面能否只交叉锥体的一面,而产生一个无限的交叉剖面?

It turns out that this is possible if and only if the plane is parallel to one of the lines making up the cone. Or, in other words, the angle between the plane and the horizon, is equal to the angle formed by a side of the cone and the horizontal plane.
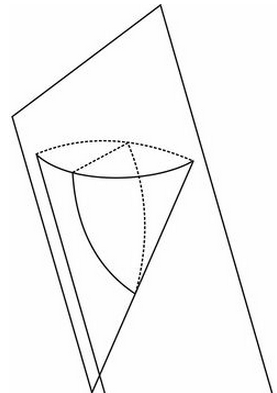
::事实证明,如果而且只有在飞机与锥形的一条线平行,或者换句话说,平面与地平线之间的角等于锥形和水平平面的侧面形成角时,这才可能发生。

In the image above, if you tilt the plane a little bit to the left it will cut off a finite ellipse (possibly a very large one if you only tilt it a little.) Tilt the plane to the right and it will intersect both sides of the cone, making a two-part conic section called a , which will be discussed in the next section.
::在上方的图像中,如果你把飞机向左倾斜一点,它就会切断一个有限的椭圆(可能是一个很大的椭圆,如果只是倾斜一点的话。 ) 将飞机向右倾斜,它会横穿锥形两侧,形成一个分为两部分的圆锥部分,称为“......”,将在下一节讨论。

When the plane is parallel to from the side of the cone, the infinite shape that results from the intersection of the plane and the cone is called a parabola. Like the ellipse, it has a number of interesting geometric properties.
::当平面与锥形的侧面平行时, 由平面和锥体交点产生的无限形状被称为抛物线。和椭圆一样, 它有一些有趣的几何特性。

The equation of a parabola is simpler than that of the ellipse. There are a couple of methods of deriving the equation of a parabola, in this lesson we explore the distance formula .
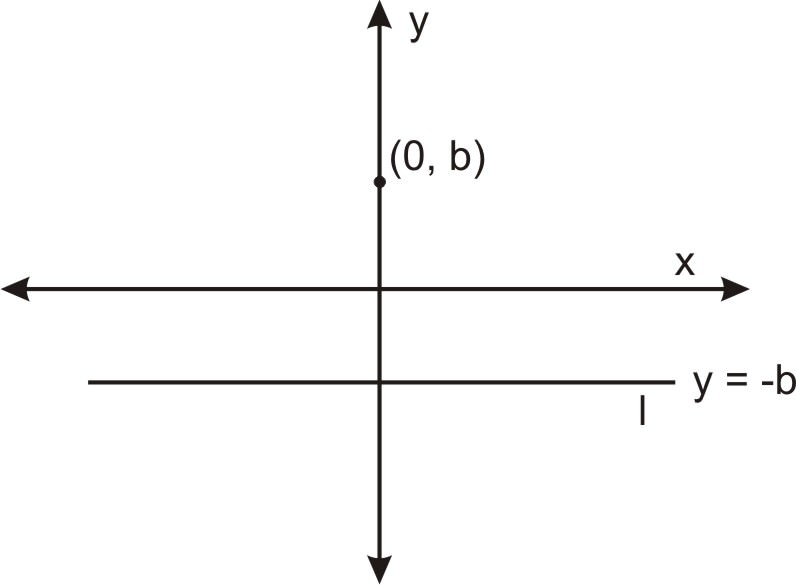
::抛物线的方程式比椭圆的方程式简单。有几种方法可以推断抛物线的方程式,在这个教训中,我们探讨距离公式。

This first method arises directly from the focus-directrix property discussed in the previous section. Suppose we have a line and a point not on that line in a plane, and we want to find the equation of the set of points in the plane that is equidistant to these two objects. Without losing any generality, we can orient the line horizontally and the point on the $\begin{align*}y-\end{align*}$ axis, with the origin halfway between them. Since the parabola is the set of points equidistant from the line and the point, The parabola passes through the origin, (0,0). The picture below shows this configuration. The point directly between the directrix and the focus (the origin in this case) is called the vertex of the parabola. Suppose the focus is located at $\begin{align*}(0,b)\end{align*}$ . Then the directrix must be $\begin{align*}y = -b\end{align*}$ .
::第一种方法直接产生于上一节所讨论的焦点方向属性。如果在平面上有一个线和一个点, 而不是该线上的一个点, 我们想要找到对等于这两个对象的平面上一组点的方程式方程式。在不丢失任何一般性的情况下, 我们可以横向调整线和y- 轴上的点, 其起点在它们之间的中间点。由于 parbola 是线和点之间的等距点组合, 抛物线通过起源点, (0,0) 。下面的图画显示了这个配置。直线和焦点( 本案的起源) 之间的点直接点被称为 parbola 的顶点。假设焦点位于 0, b 。那么直线必须是 yb 。

Thus, the parabola is the set of points $\begin{align*}(x,y)\end{align*}$ equidistant from the line $\begin{align*}y = -b\end{align*}$ and the focus point $\begin{align*}(0,b)\end{align*}$ . The distance to the line is the vertical segment from $\begin{align*}(x,y)\end{align*}$ down to $\begin{align*}(0,-b)\end{align*}$ , which has length $\begin{align*}y - ( - b) = y + b\end{align*}$ . The distance from $\begin{align*}(x,y)\end{align*}$ to the focus $\begin{align*}(0, b)\end{align*}$ is $\begin{align*}\text{distance} = \sqrt {(x - 0)^2 + (y - b)^2}\end{align*}$ by the distance formula. So the equation of the parabola is the set of points where these two distances equal.
::因此,抛物线是一系列与Yb线和焦点点(0,b)等距的点(x,y)等距。线的距离是(x,y)下至(0,-b)的垂直段,其长度为y-(-b)=y+b。从(x,y)到(0,b)的距离是距离公式的距离=(x-0)2+(y-b)2。因此,抛物线的方程式是这两个距离相等的一组点。

$\begin{aligned} y + b = \sqrt{(x - 0)^{2} + (y - b)^{2}} \end{aligned}$
$\begin{align*}y + b = \sqrt{(x - 0)^2 + (y - b)^2}\end{align*}$
::y+b=(x-0)2+(y-b)2

Since distances are always positive, we can square both sides without losing any information, obtaining the following.
::由于距离总是积极的,我们可以在不丢失任何信息的情况下,将双方平方,获得以下信息。

$\begin{aligned} y^{2} + 2 b y + b^{2} & = x^{2} + y^{2} - 2 b y + b^{2} \\ 2 b y & = x^{2} - 2 b y \\ 4 b y & = x^{2} \\ y & = \frac{1}{4 b} x^{2} \end{aligned}$
$\begin{align*} y^2 + 2by + b^2 & = x^2 + y^2 - 2by + b^2 \\ 2by & = x^2 - 2by \\ 4by & = x^2 \\ y & = \frac{1}{4b}x^2\end{align*}$
::y2+2by+2by+b2=x2+y2+y2+2by+b22by=x2-2by4by=x2y=14bx2

But $\begin{align*}b\end{align*}$ was chosen arbitrarily and could have been any positive number, and for any positive number, $\begin{align*}a,\end{align*}$ there always exists a number $\begin{align*}b\end{align*}$ such that $\begin{align*}a = \frac{1}{4b}\end{align*}$ , so we can rewrite this equation as:
::b 但被任意选择,本可以是正数,对于正数,a,总有一个数字b,a=14b,这样我们就可以改写这个等式:

$\begin{aligned} y = a x^{2} \end{aligned}$
$\begin{align*}y = ax^2\end{align*}$
::y=ax2 y=ax2 y=ax2

where $\begin{align*}a\end{align*}$ is any constant.
::其中有一个常数。

This is the general form of a parabola with a horizontal directrix, with a focus lying above it, and with a vertex at the origin. If $\begin{align*}a\end{align*}$ is negative, the parabola is reflected about the $\begin{align*}x-\end{align*}$ axis, resulting in a parabola with a horizontal directrix, with a focus lying below it, and with a vertex at the origin. The equation can be shifted horizontally or vertically by moving the vertex, resulting in the general form of a parabola with a horizontal directrix and passing through a vertex of $\begin{align*}(h,k)\end{align*}$ :
::这是具有水平直线的抛物线的一般形式,其焦点在水平直线上方,并且源头有一个顶点。如果是负的,则抛物线在 x - 轴上方反映出来,结果形成具有水平直线的抛物线,其焦点在水平直线下方,并且源头有一个顶点。公式可以通过移动顶点而横向或垂直移动,从而形成带有水平直线的抛物线的一般形式,然后通过(h,k)的顶点:

$\begin{aligned} y - k = a (x - h)^{2} \end{aligned}$
$\begin{align*}y - k = a(x - h)^2\end{align*}$
::y-k=a(x-h)2

Switching $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ , the equation for a parabola with a vertical directrix and with a vertex at $\begin{align*}(h,k)\end{align*}$ is:
::切换 x 和 y, 具有垂直直线和(h, k) 点有顶点的抛物线方程式的方程式是:

$\begin{aligned} x - h = a (y - k)^{2} \end{aligned}$
$\begin{align*}x - h = a(y - k)^2\end{align*}$
::x-h=a(y-k)2

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about the limitation on the angle of the slice taken out of one of the cones if you only wanted a parabola.
::早些时候,有人问你一个问题切片角从锥锥中取出时的极限如果你只想要一个抛物线的话

In order to only get a parabola cross section, the slice must be taken at the same angle as the side of the cone, that way the edge of the slice runs parallel to the edge of the cone and never intersects it at either top or bottom.
::为了只获得一个抛物线横截面,切片必须与锥形的侧面持同一角度,这样,切片的边缘就会与锥形的边缘平行,而不会在顶部或底部交叉。

This can be seen by a close look at the image from above:
::仔细观察上面的图像即可看出这一点:

Example 2
::例2

Sketch a graph of the parabola $\begin{align*}y = 3x^2 + 12x + 17\end{align*}$ .
::绘制抛物线 y= 3x2+12x+17的图。

First, we need to factor out the coefficient of the $\begin{align*}x^2\end{align*}$ term and complete the square:
::首先,我们需要将x2术语的系数计算出来, 并完成方形 :

$\begin{aligned} y & = 3 (x^{2} + 4 x) + 17 \\ y & = 3 (x^{2} + 4 x + 4) + 17 - 12 \\ y & = 3 (x + 2)^{2} + 5 \end{aligned}$
$\begin{align*}y & = 3(x^2 + 4x) + 17 \\ y & = 3(x^2 + 4x + 4) + 17 - 12 \\ y & = 3(x + 2)^2 + 5\end{align*}$
::y=3(x2+4x)+17y=3(x2+4x+4)+17-12y=3(x+2)2+5

Now we write it in the form $\begin{align*}y - k = a(x - h)^2\end{align*}$ :
::现在,我们把它写成y-k=a(x-h)2:

$\begin{aligned} y - 5 = 3 (x + 2)^{2} \end{aligned}$
$\begin{align*}y - 5 = 3(x + 2)^2\end{align*}$
::y-5=3(x+2)2

So the vertex is at $\begin{align*}(-2, 5)\end{align*}$ and plotting a few $\begin{align*}x-\end{align*}$ values on either side of $\begin{align*}x = -2\end{align*}$ , we can draw the following sketch of the parabola:
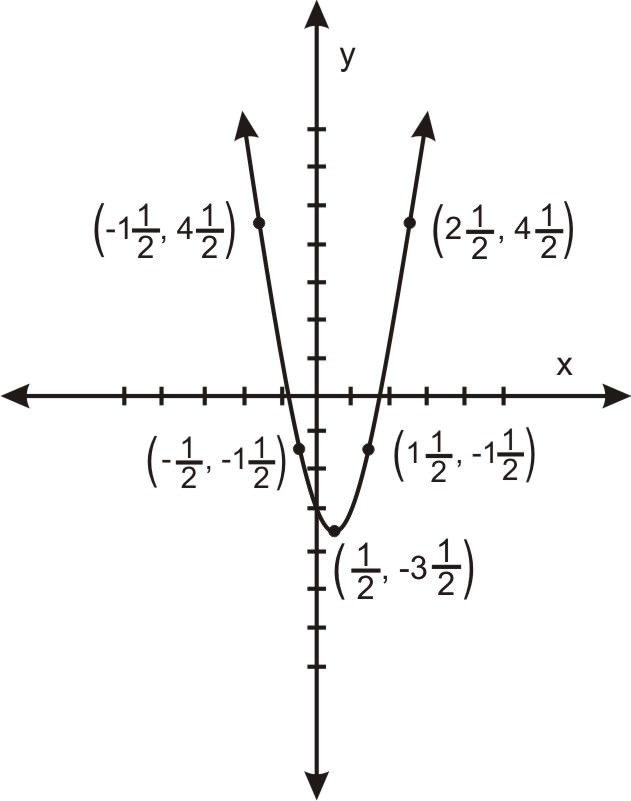
::因此,顶点在(-2,5),在 x2 的两侧绘制几个x-值,我们可以绘制抛物线的如下草图:

Example 3
::例3

Sketch a graph of the following parabola: $\begin{align*}y = 2x^2 - 2x - 3\end{align*}$ .
::绘制下列抛物线的图:y=2x2-2x-3。

Factor out the 2 : $\begin{align*}y = 2(x^2 - x ) -3\end{align*}$
::乘以 2 : Y=2( x2- x) - 3

Complete the square: $\begin{align*}y + \frac{1}{2} = 2(x^2 -x + \frac{1}{4}) -3\end{align*}$
::完成正方形: Y+12=2( x2- x+14)- 3

Add 3 to both sides and factor the trinomial: $\begin{align*} y + 3 \frac{1}{2} = 2(x - \frac{1}{2})^2\end{align*}$
::将三边加3和三边因素:y+312=2(x-12)2

The vertex (h, k) is: $\begin{align*}(\frac{1}{2}, -3 \frac{1}{2})\end{align*}$
::顶点(h、k)为: (12,-312)

Plot a couple of points to get:
::绘制几个点以获得:

Example 4
::例4

Sketch a graph of the following parabola: $\begin{align*}3x^2 + 12x + 11 - y = 0\end{align*}$ .
::绘制下列抛物线的图: 3x2+12x+11-y=0。

Factor out the 3 and move y and 11: $\begin{align*}3(x^2 + 4x ) = y - 11\end{align*}$
::乘以 3 , 移动 Y 和 11 : 3( x2+4x) =y- 11

Complete the square: $\begin{align*}3(x^2 + 4x +4) = y -11 + 12\end{align*}$
::完成方形: 3( 3x2+4x+4) =y- 11+12

Factor the trinomial and collect like terms: $\begin{align*}3(x + 2)^2 = y + 1\end{align*}$
::乘以三角数并收集类似术语: 3( 3( x+2) 2=y+1)

The vertex (h, k) is at: $\begin{align*}(-2, -1)\end{align*}$
::顶部( h, k) 值-2, - 1) 。

Plot a couple of points to get:
::绘制几个点以获得:

Example 5
::例5

Identify which of the following equations are :
::标明下列哪些方程式:

$\begin{align*}y - 5x + x^2 = 3\end{align*}$
::y-5x+x2=3 y- 5x+x2=3

$\begin{align*}x^2 - 3y^2 + 3y - 2x + 15 = 0\end{align*}$
::x2-3y2+3y-2x+15=0

$\begin{align*}x - 6y^2 + 20x - 100 = 0\end{align*}$
::x-6y2+20x-100=0

Recall that a parabola has a squared input term only :
::回顾抛物线只有方形输入术语:

Since b. $\begin{align*}x^2 - 3y^2 + 3y - 2x + 15 = 0\end{align*}$ is squared on the input and output (in other words, both x and y are squared), it is not a parabola.
::b. x2-3y2+3y-2x+15=0在输入和输出上方形(换言之,x和y是正方形),因此它不是一个抛物线。

a. $\begin{align*}y - 5x + x^2 = 3 \end{align*}$ and c. $\begin{align*}x - 6y^2 + 20x - 100 = 0\end{align*}$ are both parabolas.
::a. y-5x+x2=3和c. x-6y2+20x-100=0是两个参数。

By the way, after completing the square, equation a factors as: $\begin{align*}(x - 1)^2 - 3(y - \frac{1}{2})^2 + 14 \frac{3}{4} = 0\end{align*}$ .
::顺便说一句,在完成正方形后,方程式因数为x-1)2-3(y-12)2+1434=0。

Example 6
::例6

Calculate the distance between (3, 4) and (9, 5).
::计算距离(3,4)和(9,5)之间的距离。

To calculate the distance between (3, 4) and (9, 5), use the distance formula $\begin{align*}\text{distance} = \sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2}\end{align*}$ :
::要计算(3,4)和(9,5)之间的距离,请使用距离公式的距离=(x2-x1)2+(y2-y1)2:

$\begin{align*}\text{distance} = \sqrt {(9 - 3)^2 + (5 - 4)^2}\end{align*}$ ..... Substitute
::距离=(9-3)2+(5-4)2。替代物

$\begin{align*}\text{distance} = \sqrt {(6)^2 + (1)^2}\end{align*}$ ..... Simplify
::距离=(6)2+(1)2...。简化

$\begin{align*}\text{distance} = \sqrt {36 + 1} \to \sqrt{37}\end{align*}$
::距离=36+1___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{align*}\therefore \sqrt{37}\end{align*}$ is the distance between (3, 4) and (9, 5).
::37是(3,4)和(9,5)之间的距离。

Example 7
::例7

Calculate the distance between (-2, 7) and (11, 23).
::计算 (-2, 7) 和 (11, 23) 之间的距离。

To calculate the distance between (-2, 7) and (11, 23), use the distance formula $\begin{align*}\text{distance} = \sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2}\end{align*}$ :
::要计算 (-2, 7) 和 (11, 23) 之间的距离, 请使用距离公式的距离= (x2 - x1) 2+ (y2 -y1) 2 :

$\begin{align*}\text{distance} = \sqrt {(11 - (-2))^2 + (23 - 7)^2}\end{align*}$ ..... Substitute
::距离=( 11 - (-2)) 2+( 23 - 7) 2 .... 替代物

$\begin{align*}\text{distance} = \sqrt {(13)^2 + (16)^2}\end{align*}$ ..... Simplify
::距离=( 13) 2+( 16) 2 ..... 简化

$\begin{align*}\text{distance} = \sqrt {169 + 256} \to \sqrt{425} \to 5\sqrt{17}\end{align*}$
::距离=169+256_425_517

$\begin{align*}\therefore 5\sqrt{17}\end{align*}$ is the distance between (-2, 7) and (11, 23).
::517是(-2、7)和(11、23)之间的距离。

Review
::回顾

Graph the following:
::图表如下:

$\begin{align*}y = -3(x - 1)^2 + 2\end{align*}$
::y3 (x- 1) 2+2

$\begin{align*}y = 3(x - 1)^2 - 1\end{align*}$
::y=3 (x- 1) 2-2- 1

$\begin{align*}x = -2(y + 2)^2 - 1\end{align*}$
::x2(y+2)2-2-1

$\begin{align*}y = 3(x + 4)^2 - 1\end{align*}$
::y=3( x+4) 2- 1

$\begin{align*}y = (x - 3)^2\end{align*}$
::y= (x-3) 2

%5E2%20%2B%201"> $\begin{align*}x = -3(y)^2 + 1\end{align*}$
::x32+1

$\begin{align*}x = -(y - 3)^2 - 4\end{align*}$
::x(y-3)2-4

$\begin{align*}x = -3(y - 4)^2 + 4\end{align*}$
::x3(y- 4) 2+4

$\begin{align*}y = 2(x + 3)^2 - 3\end{align*}$
::y=2( x+3) 2- 3

$\begin{align*}x = (y - 1)^2 - 2\end{align*}$
::x= (y- 1) 2-2

For questions 11-20, imagine a limited cone (not infinitely tall), as pictured below. Assume the two coordinates listed represent the intersection of a parabolic curve and the top of the cone. If the top surface of the cone were represented by the x -axis, then the two coordinates could be considered the x -intercepts of the equation of the parabola. Find the distance between the points, and where required, the coordinates of the points.
::对于问题11-20, 想象一个有限的锥体( 不无限高) , 如下图所示。假设列出的两个坐标代表抛光曲线和锥体顶部的交叉点。如果锥体的顶部表面由 x 轴代表, 那么这两个坐标可以被视为抛光线方程的 x 截点。找出点之间的距离, 并在必要时找到点的坐标。

Coordinates: (-20, -17) and (6, -1)
::坐标20,-17)和(6,-1)

Coordinates: (-1, -5) and (6, -13)
::坐标-1,5)和(6,13)

Coordinates: (1, 2) and (5, -5)
::座标1,2)和(5,5)

Coordinates: (13, 12) and (15, 6)
::坐标13、12)和(15、6)

Coordinates: (3, 9) and (6, -14)
::坐标3,9)和(6,14)

$\begin{align*}-25x^2 + 15x + 10 = 0\end{align*}$
::- 25x2+15x+10=0

$\begin{align*}-24x^2 + 22x -4 = 0\end{align*}$
::- 24x2+22x-4=0

$\begin{align*}4x^2 -24x + 32 = 0\end{align*}$
::4x2 - 24x+32=0

$\begin{align*}24x^2 + 54x + 27 = 0\end{align*}$
::24x2+54x+27=0

$\begin{align*}12x^2 + 25x + 12 = 0\end{align*}$
::12x2+25x+12=0

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Parabolas and the Distance Formula ::Parabolas和距离公式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)

Parabolas and the Distance Formula
::Parabolas和距离公式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Review
::回顾

Review (Answers)
::回顾(答复)