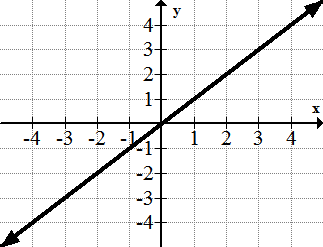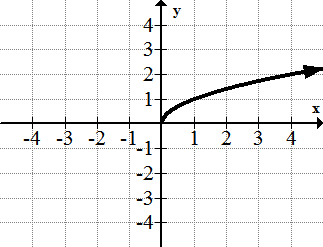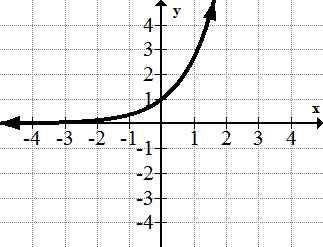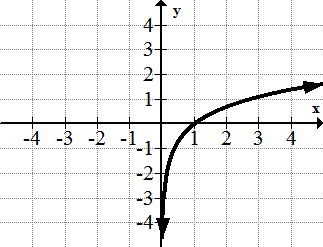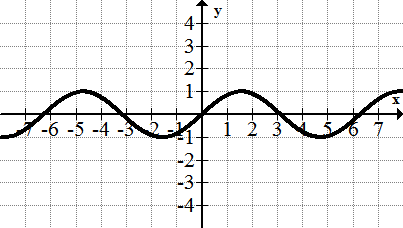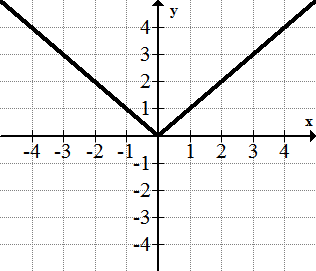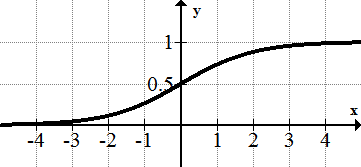家庭功能

播放段落

Functions come in all different shapes. A few are very closely related and others are very different, but often confused. For example, what is the difference between $\begin{align*}x^2\end{align*}$  and $\begin{align*}2^x?\end{align*}$  They both have an $\begin{align*}x\end{align*}$  and a 2 and they both equal 4 when $\begin{align*}x=2,\end{align*}$  but one eventually becomes much bigger than the other. 
::函数以所有不同的形状出现。 少数函数非常密切关联, 另一些函数则非常不同, 但往往混淆不清。 例如, x2 和 2x 之间有什么区别? 它们都有 x 和 2 , 当 x=2 时, 它们都等于 4, 但一个最终会比另一个大得多 。

播放段落

If mathematicians are cooks, then families of functions are their ingredients. Each family of functions has its own flavor and personality. Before you learn to combine functions to create an infinite number of potential models, you need to get a clear idea of the name of each function family and how it acts. 
::如果数学家是厨师,那么功能家庭就是其成份。每个功能家庭都有自己的口味和个性。在学会组合功能创造无限数量的潜在模型之前,你需要清楚了解每个功能家庭的名称及其行为方式。

播放段落

The Identity Function:  $\begin{align*}f(x)=x\end{align*}$
::身份函数: f(x)=x

播放段落

The identity function is the simplest function and all straight lines are transformations of the identity function family. 
::身份功能是最简单的功能,所有直线都是身份功能家族的转换。

播放段落

The Squaring Function:  $\begin{align*}f(x)=x^2\end{align*}$
::Sqaling 函数: f( x)=x2

播放段落

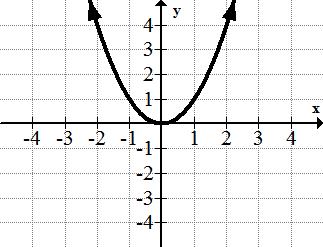
The squaring function (quadratic function)  is commonly called a parabola and is useful for modeling the motion of falling objects. All are transformations of this squaring function. 
::方位函数( 方位函数) 通常被称为抛物线, 可用于模拟落落物体的移动。 均是此方位函数的转换 。

播放段落

The Cubing Function: $\begin{align*}f(x)=x^3\end{align*}$

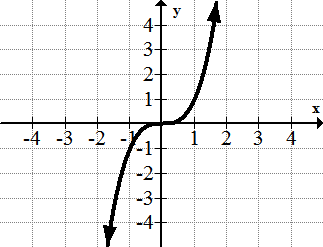
::Cubing 函数: f(x)=x3

播放段落

The cubing function has a different kind of than the squaring function. Since volume is measured in cubic units, many physics applications use the cubic function. 
::孵化函数与对角函数有不同类型。由于体积用立方体单位测量,许多物理应用都使用立方体函数。

播放段落

The Square Root Function :  $\begin{align*}f(x)=\sqrt{x}=x^{\frac{1}{2}}\end{align*}$
::平方根函数: f( x)=x=x12

播放段落

The square root function is not defined over all real numbers. It introduces the possibility of and is also closely related to the squaring function. 
::平方根函数不是对所有实际数字定义的,它引入了划分函数的可能性,并且也与该函数密切相关。

播放段落

The Reciprocal Function:  $\begin{align*}f(x)=x^{-1}=\frac{1}{x}\end{align*}$
::互惠函数: f(x)=x-1=1x

播放段落

The reciprocal function is also known as a and a rational function . It has two parts that are disconnected and is not defined at zero. Simple electric circuits are modeled with the reciprocal function. 
::互惠功能也被称为一种理性功能,它有两个部分是断开的,没有被确定为零。 简单的电路以互惠功能为模型。

播放段落

A ll the functions listed so far can be grouped together into an even larger function family called the power function family. 
::迄今列出的所有功能可归为更大的功能家庭,称为权力功能家庭。

播放段落

The Power Function Family:  $\begin{align*}f(x)=cx^a\end{align*}$
::Power 函数家庭: f(x) = cxa

播放段落

The power function family has two parameters. The parameter $\begin{align*}c\end{align*}$  is a vertical scale factor . The parameter $\begin{align*}a\end{align*}$  controls everything about the shape. The reason why all the functions listed so far are subsets of the larger power function family is because they only differ in their value of $\begin{align*}a.\end{align*}$  The power function family also shows you that there are an infinite number of other functions like quartics  $\begin{align*}(f(x)=x^4)\end{align*}$ and quintics  $\begin{align*}(f(x)=x^5)\end{align*}$ that don’t really need whole categories of their own. The power function family can be extended to create and rational functions. 
::权力函数家族有两个参数。 参数 c 是一个垂直比例系数。 参数控制着形状上的所有函数。 迄今列出的所有函数都是较大权力函数家族子集的原因, 是因为这些函数的值存在差异。 权力函数家族也向您表明, 有无限数量的其他函数, 如 Quertic (f( x)=x4) 和 quintic (f( x)=x5) , 并不真正需要它们自己的整个类别。 权力函数家族可以扩展为创建和理性功能 。

播放段落

The Exponential Function Family:  $\begin{align*}f(x)=e^x\end{align*}$
::指数函数家族: f(x) =ex

播放段落

The exponential function family is one of the first functions you see where $\begin{align*}x\end{align*}$  is not the base of the exponent . This function eventually grows much faster than any power function.  $\begin{align*}f(x)=2^x\end{align*}$ is a very common exponential function. Many applications  in biology and finance require the use of . 
::指数函数族是您看到的第一个函数之一, x 不是指数的底部。 此函数最终会比任何功率函数增长更快。 f( x)=2x是一个非常常见的指数函数。 生物学和金融的许多应用都需要使用 。

播放段落

The Logarithm Function: $\begin{align*}f(x)=\ln x\end{align*}$

::对数函数: f(x)=lnx

播放段落

The logarithmic function is closely related to the exponential function family. Many people confuse the graph of the log function with the square root function. Careful analysis shows several important differences. The log function is the basis for the Richter Scale which is how earthquakes are measured. 
::对数函数与指数函数家族密切相关。许多人将日志函数的图形与平方根函数混为一谈。仔细分析显示若干重要的差异。日志函数是测算地震的Richter规模的基础。

播放段落

The Periodic Function Family: $\begin{align*}f(x)=\sin x\end{align*}$

::周期函数家庭: f(x)=sinx

播放段落

The sine graph is one of many periodic functions. Periodic refers to the fact that the sine wave repeats a cycle for every period of time. Periodic functions are extremely important for modeling tides and other real world phenomena. 
::正弦图是许多周期函数之一。 周期是指正弦波每一段时间重复一个周期。 周期函数对于模拟潮汐和其他真实世界现象极为重要 。

播放段落

The Absolute Value Function: $\begin{align*}f(x)=|x|\end{align*}$

::绝对值函数 : f(x)

播放段落

The absolute value function is one of the few basic functions that is not totally smooth. 
::绝对值函数是少数不完全平稳的基本函数之一。

播放段落

The Logistic Function : $\begin{align*}f(x)=\frac{1}{1+e^{-x}}\end{align*}$

::后勤职能:f(x)=11+e-x

播放段落

The logistic function is a combination of the exponential function and the reciprocal function. This curve is very powerful because it models population growths where the maximum population is limited by environmental resources. 
::物流功能是指数函数和对等函数的组合,这一曲线非常强大,因为它模拟人口增长,而人口的最大数量受环境资源的限制。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were given a problem about comparing $\begin{align*}x^2\end{align*}$  and  $\begin{align*}2^x.\end{align*}$  While $\begin{align*}x^2\end{align*}$  and $\begin{align*}2^x\end{align*}$  have similar ingredients, they have very different graphical features. The squaring function is symmetric about the line $\begin{align*}x=0\end{align*}$  while the exponential function is not. When $\begin{align*}x=0\end{align*}$ , the squaring function has a height of zero and the exponential function has a height of one. The squaring function has a that becomes steeper as $\begin{align*}x\end{align*}$  gets further from the origin while the exponential function flattens as $\begin{align*}x\end{align*}$  gets further from 0 in the negative direction . All of these differences are important and not obvious at first glance. 
::早些时候,您遇到一个比较 x2 和 2x 的问题。 虽然 x2 和 2x 的成分相似, 但具有非常不同的图形特征。 对比函数对齐了 x=0 线, 而指数函数则不是。 当 x=0 时, 对比函数的高度为零, 指数函数的高度为1。 当x从源头往后走, 而指数函数从 0 向底向向向下向下向下向下倾斜时, 方函数会变陡。 所有这些差异都很重要, 初看起来并不明显 。

播放段落

Which functions always have a positive slope over the entire real line? 
::哪个函数在整个实际线上总是有一个正斜坡?

播放段落

  $\begin{align*}y=x, y=e^x, y=\frac{1}{1+e^{-x}}.\end{align*}$  Some functions that are close but not quite:  $\begin{align*}y=x^3, y=\sqrt{x}\end{align*}$
::y=x,y=ex,y=11+e-x。有些函数接近但不太接近:y=x3,y=x

播放段落

Example 3
::例3

播放段落

Compare and contrast the graphs of the two functions: 
::比较和对比两个函数的图形:

播放段落

  $\begin{align*}f(x)=\ln x\end{align*}$  and   $\begin{align*}h(x)= \sqrt{x}\end{align*}$
:xx) = lnx 和 h(x) =x

播放段落

Similarities: Both functions increase without bound as $\begin{align*}x\end{align*}$  gets larger. Both functions are not defined for negative numbers. 
::相似点: 两项功能均在增加, 但没有被约束, 因为 x 越大。 这两种功能没有被定义为负数 。

播放段落

Differences: The log function approaches negative infinity as $\begin{align*}x\end{align*}$  approaches 0. The square root function, on the other hand, just ends at the point (0, 0). 
::差异:日志函数在x接近0时接近负无限值。而平方根函数则在点(0,0)处结束。

播放段落

Example 4
::例4

播放段落

Describe the symmetry among the function families discussed in this concept. Consider both reflection symmetry and rotational symmetry.
::描述这个概念中讨论的功能家庭之间的对称性。 既考虑反射对称性,也考虑旋转对称性。

播放段落

Some function families have reflective symmetry with themselves:
::一些函数族与它们有反射对称性:

播放段落

$\begin{align*}y=x, y=x^2, y=\frac{1}{x}, y=|x|\end{align*}$
::y=x2,y=1x,y=xx

播放段落

Some function families are rotationally symmetric:
::一些函数族是旋转对称的 :

播放段落

$\begin{align*}y=x, y=x^3, y=\frac{1}{x},y=\sin x, y=\frac{1}{1+e^{-x}}\end{align*}$
::y=x3,y=1x,y=sinx,y=11+e-x

播放段落

Some pairs of function families are full or partial reflections of other function families:
::有些功能家庭是其他功能家庭的全部或部分反映:

播放段落

$\begin{align*}y = x^2, y=\sqrt{x}\end{align*}$
::y=x2,y=x

播放段落

$\begin{align*}y = e^x, y=\ln x\end{align*}$
::y=ex,y=in=x y=x y=ex y=x y=x

Summary

播放段落 The Power Function Family includes the identity function, squaring function, cubing function, square root function, and reciprocal function. ::Power Company Family包括身份功能、配方功能、孵化功能、平方根功能和对等功能。 播放段落 The Exponential Function Family includes the exponential function. ::指数函数家族包括指数函数。 播放段落 The logarithmic function is closely related to the exponential function family ::对数对数函数与指数函数家族密切相关 播放段落 The Periodic Function Family includes trigonometry functions such as sine and cosine. ::" 定期功能家庭 " 包括三角函数,如正弦和共弦。

播放段落

For 1-10, sketch a graph of the function from memory.
::对于 1- 10, 从内存绘制函数图示 。

播放段落

1.  $\begin{align*}y = e^x\end{align*}$
::1. y=ex

播放段落

2.  $\begin{align*}y= \ln (x)\end{align*}$
::2.y=ln(x)

播放段落

3.  $\begin{align*}y= \sin (x)\end{align*}$
::3.y=sin(x)

播放段落

4.  $\begin{align*}y= x^2\end{align*}$
::4. y=x2

播放段落

5.  $\begin{align*}y= |x|\end{align*}$
::5 y x

播放段落

6.  $\begin{align*}y = \frac{1}{x}\end{align*}$
::6. y=1x

播放段落

7.  $\begin{align*}y = \frac{1}{1+e^{ - x}}\end{align*}$
::7. y=11+e-x

播放段落

8.  $\begin{align*}y = \sqrt{x}\end{align*}$
::8.y=x 8y=x

播放段落

9. $\begin{align*}y = x^3\end{align*}$
::9. y=x3

播放段落

10. $\begin{align*}y = x\end{align*}$
::10.y=x

播放段落

11. Which function is not defined at 0? Why?
::11. 哪个职能不是在0点界定的?为什么?

播放段落

12. Which functions are bounded below but not above?
::12. 哪些职能的界限是低于但不高于这些职能?

播放段落

13. What are the differences between  $\begin{align*}y = x^2\end{align*}$ and $\begin{align*}y = x^3\end{align*}$ ?
::13. y=x2和y=x3之间有什么区别?

播放段落

14. What is a similarity between $\begin{align*}y = e^x\end{align*}$  and $\begin{align*}y = \ln (x)\end{align*}$ ?
::14. y=ex和y=ln(x)之间有什么相似之处?

播放段落

15. Explain why $\begin{align*}y = \sqrt{x}\end{align*}$  is not defined for all values of $\begin{align*}x\end{align*}$ .
::15. 解释为什么y=x没有为 x 的所有值定义。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。