特别右三角

播放段落

The Pythagorean Theorem is great for finding the third side of a right triangle when you already know two other sides. There are some triangles like 30-60-90 and 45-45-90 triangles that are so common that it is useful to know the side ratios without doing the Pythagorean Theorem each time. Using these patterns also allows you to totally solve for the missing sides of these special triangles when you only know one side length.
::Pytagorean Theorem 在您已经知道另外两面的情况下, 发现右三角的第三面非常适合。 有些三角形, 如 30- 60- 90 和 45- 45- 45- 90 三角形, 十分常见, 以至于在每次不做 Pytagorean Theorem 的情况下了解侧比是有用的 。 使用这些模式还可以让您完全解答这些特殊三角形中缺失的两边, 当您只知道一个侧长时 。

播放段落

Given a 45-45-90 right triangle with sides 6 inches, 6 inches and $\begin{align*}x \ \text{inches}\end{align*}$ , what is the value of $\begin{align*}x\end{align*}$ ? 
::鉴于一个45-45-90右三角形,侧边6英寸、6英寸和x英寸,x值是多少?

播放段落

Special Right Triangles
::特别右三角

播放段落

There are three types of special right triangles, 30-60-90 triangles, 45-45-90 triangles, and Pythagorean triple triangles.
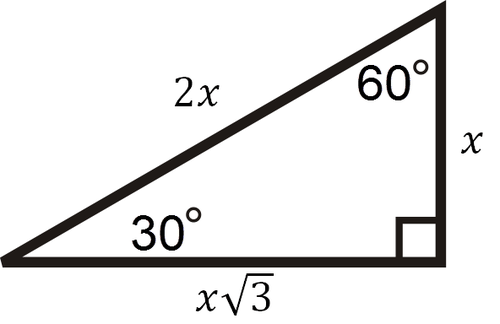
::有三种特殊右三角, 30-60-90三角, 45-45-90三角, 还有毕达哥伦三角。

播放段落

30-60-90 Triangles
::30-60-90三角

播放段落

A 30-60-90 right triangle has side ratios $\begin{align*}x, x \sqrt{3}, 2x\end{align*}$ . 
::右三角形30 -60 -90的侧翼比率xxx3,2x。

播放段落

Confirm with :
::确认:

播放段落

$$\begin{align*}x^2 + \left ( x \sqrt{3} \right )^2 & = (2x)^2\\ x^2 + 3x^2 & = 4x^2\\ 4x^2 & = 4x^2\end{align*}$$
::x2+( x3) 2=( 2x) 2x2+3x2=4x24x2=4x2

播放段落

45-45-90 Triangles
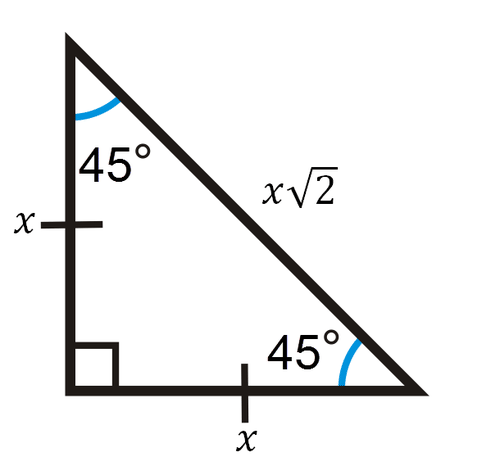
::45-45-90三角

播放段落

A 45-45-90 right triangle has side ratios $\begin{align*}x, x, x \sqrt{2}\end{align*}$ . 
::45 -45 -90右三角形有侧翼比率xxxxxx2。

播放段落

Confirm with Pythagorean Theorem:
::与毕达哥里安理论确认:

播放段落

 

$$\begin{align*}x^2 + x^2 & = \left ( x \sqrt{2} \right )^2\\ 2x^2 & = 2x^2\end{align*}$$
::x2+x2=(x2)22x2=2x2

播放段落

Note that the order of the side ratios $\begin{align*}x, x \sqrt{3}, 2x\end{align*}$  and $\begin{align*}x, x, x \sqrt{2}\end{align*}$  is important because each side ratio has a corresponding angle . In all triangles, the smallest sides correspond to smallest angles and largest sides always correspond to the largest angles.
::请注意, 侧比 x, x3, 2x 和 x, x, x, x2 的顺序很重要, 因为侧比每个侧比都有相应的角度。 在所有三角形中, 最小边对应最小角度, 最大边总是对应最大角度 。

播放段落

Pythagorean Triple Triangles
::毕达哥里亚三三角

播放段落

Pythagorean number triples are special right triangles with integer sides. While the angles are not integers, the side ratios are very useful to know because they show up everywhere. Knowing these number triples also saves a lot of time from doing the Pythagorean Theorem repeatedly. Here are some examples of Pythagorean number triples:
::Pythagorean 数字的三倍是带有整数边的特殊右三角形。 虽然角度不是整数, 但侧比非常有用, 因为它们无处可见。 了解这些数字的三倍也会节省很多时间, 而不是反复使用 Pytagorean Theorem 。 以下是一些Pytagorean 数字的三倍例子 :

• 3, 4, 5
• 5, 12, 13
• 7, 24, 25
• 8, 15, 17
• 9, 40, 41

播放段落

More Pythagorean number triples can be found by scaling any other Pythagorean number triple . For example:
::通过将任何其他的毕达哥里数字扩大至三倍,可以发现更多毕达哥里数字的三倍。例如:

播放段落

$\begin{align*}3, 4, 5 \rightarrow 6, 8, 10\end{align*}$ (scaled by a factor of 2)
::3,4,56,8,10(乘以2)

播放段落

Even more Pythagorean number triples can be found by taking any odd integer like 11, squaring it to get 121, halving the result to get 60.5. The original number 11 and the two numbers that are 0.5 above and below (60 and 61) will always be a Pythagorean number triple.
::通过使用11这样的奇数整数,可以发现更多的毕达哥里数字三倍。 将整数分成121个,将结果减半,将60.5个。 原数11和2个数字在0.5以上或以下(60和61)将永远是毕达哥里数字的三倍。

$\begin{align*}11^2 + 60^2 = 61^2\end{align*}$

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier you were asked about a 45-45-90 right triangle with sides 6 inches, 6 inches and $\begin{align*}x\end{align*}$  inches. If you can recognize the pattern for , a right triangle with legs 6 inches and 6 inches has a hypotenuse that  is $\begin{align*}6 \sqrt{2} \ \text{inches}\end{align*}$ .   $\begin{align*}x=6\sqrt{2}\end{align*}$ .
::早些时候有人问您一个45-45-90右三角形,侧边有6英寸、6英寸和x英寸。如果您能够辨认出 6 英寸和6 英寸的右三角形,右三角形的腿部有6英寸和6 英寸,下限为 62 英寸 x= 62 。

播放段落

Example 2
::例2

播放段落

A 30-60-90 right triangle has hypotenuse of length 10. What are the lengths of the other two sides? 
::右三角形30-60-90的长度为10,其他两边的长度是多少?

播放段落

The hypotenuse is the side opposite 90. Sometimes it is helpful to draw a picture or make a table. 
::低温是90对面的一面,有时绘制图片或制作一张桌子是有用的。

30	60	90
播放段落 $\begin{align*}x\end{align*}$ ::x x	播放段落 $\begin{align*}x \sqrt{3}\end{align*}$ ::x3x3	播放段落 $\begin{align*}2x\end{align*}$ ::2x 2x
		10

播放段落

From the table you can write very small subsequent equations to solve for the missing sides. 
::您可以在表格中写出非常小的后继方程式, 以解析缺失的方程式 。

播放段落

$$\begin{align*}10 & = 2x\\ x & = 5\\ x \sqrt{3} & = 5 \sqrt{3}\end{align*}$$
::10=2xx=5x3=53

播放段落

The other sides are  $\begin{align*}5\end{align*}$  and  $\begin{align*}5\sqrt{3}\end{align*}$ .
::另一方是5和53

播放段落

Example 3
::例3

播放段落

A 30-60-90 right triangle has a side length of 18 inches corresponding to 60 degrees. What are the lengths of the other two sides? 
::右三角形30-60-90的侧长为18英寸,相当于60度。其他两边的长度是多少?

播放段落

Make a table with the side ratios and the information given, then write equations and solve for the missing side lengths. 
::绘制带有侧比和所提供信息的表格,然后写入方程式,并解决缺失的侧边长度。

30	60	90
播放段落 $\begin{align*}x\end{align*}$ ::x x	播放段落 $\begin{align*}x \sqrt{3}\end{align*}$ ::x3x3	播放段落 $\begin{align*}2x\end{align*}$ ::2x 2x
	18

播放段落

$$\begin{align*}18 & = x \sqrt{3}\\ \frac{18}{\sqrt{3}} & = x\\ x & = \frac{18}{\sqrt{3}} = \frac{18}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{18 \sqrt{3}}{3} = 6 \sqrt{3}\\ x &= 6 \sqrt{3}\end{align*}$$
::18=x3183=xx=183=183=1883=1833=1833=63x=63

播放段落

Note that you need to rationalize denominators.
::请注意,你需要 合理化的分母。

播放段落

Now use the calculated  $\begin{align*}x\end{align*}$  value to solve for  $\begin{align*}2x\end{align*}$ .
::现在使用计算好的 x 值解析 2x 。

播放段落

$$\begin{align*}2x &= 2(6 \sqrt {3})\\ 2x &= 12 \sqrt {3}\end{align*}$$
::2x=2( 2- 632x=123)

播放段落

The other sides are  $\begin{align*}6\sqrt{3}\end{align*}$  and  $\begin{align*}12\sqrt{3}\end{align*}$ .
::其他方面为63和123。

播放段落

Example 4
::例4

播放段落

Using your knowledge of special right triangle ratios, solve for the missing sides of the right triangle.
::使用您对特殊右三角比的知识, 解决右三角间缺失的边 。

播放段落

The other sides are each $\begin{align*}\frac{5 \sqrt{2}}{2}\end{align*}$ .
::另一边是522号

45	45	90
播放段落 $\begin{align*}x\end{align*}$ ::x x	播放段落 $\begin{align*}x\end{align*}$ ::x x	播放段落 $\begin{align*}x \sqrt{2}\end{align*}$ ::x2x2
		5

播放段落

$$\begin{align*}x \sqrt{2} & = 5\\ x & = \frac{5}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{5 \sqrt{2}}{2}\end{align*}$$
::x2=5x=52=22=522

播放段落

The other sides are each  $\begin{align*}\frac{5\sqrt{2}}{2}\end{align*}$ .
::另一边是522号

播放段落

Example 5
::例5

播放段落

Using your knowledge of special right triangle ratios, solve for the missing sides of the right triangle.
::使用您对特殊右三角比的知识, 解决右三角间缺失的边 。

播放段落

The other sides are 9 and $\begin{align*}6 \sqrt{3}\end{align*}$ .
::其他方面为9和63。

30	60	90
播放段落 $\begin{align*}x\end{align*}$ ::x x	播放段落 $\begin{align*}x \sqrt{3}\end{align*}$ ::x3x3	播放段落 $\begin{align*}2x\end{align*}$ ::2x 2x
$\begin{align*}3 \sqrt{3}\end{align*}$

播放段落

$$\begin{align*}x & = 3 \sqrt{3}\\ 2x & = 6 \sqrt{3}\\ x \sqrt{3} & = 3 \sqrt{3} \cdot \sqrt{3} = 9\end{align*}$$
::x=332x=63x3=333=9

播放段落

The other sides are  $\begin{align*}9\end{align*}$  and  $\begin{align*}6\sqrt{3}\end{align*}$ .
::其他方面为9和63。

Summary

播放段落 There are three types of special right triangles . 播放段落 30-60-90 triangles have side ratios of $\begin{align*}x,x\sqrt{3},2x.\end{align*}$   ::30-60-90三角形的侧翼比率为x,x3,2x。 播放段落 45-45-90 triangles have side ratios of $\begin{align*}x,x,x\sqrt{2}.\end{align*}$   ::45-45-90三角形的侧翼比率为x、x、x2。 播放段落 Pythagorean triple triangles have integer side lengths and include examples such as (3, 4, 5), (5, 12, 13), and (7, 24, 25). ::毕达哥伦三角形的侧长为整数,例如(3、4、5、5、5、12、13)和(7、24、25)。 ::有三种类型的特殊右三角。 30-60-90三角形的侧翼比率为 x,x3,2x. 45-45-90三角形的侧翼比率为 x,x,x,x2,Pythagoren三角形的侧翼比率为x,x,x,x2,双长整数,例如(3,4,5,5,5,12,13)和(7,24,25)。

播放段落

Review
::回顾

播放段落

For 1-4, find the missing sides of the 45-45-90 triangle based on the information given in each row.
::1-4,根据每行提供的信息,找到45-45-90三角形的缺失侧。

播放段落 Problem Number ::问题编号	播放段落 Side Opposite $\begin{align*}45^\circ\end{align*}$ ::侧面45号对面____________________________________________________________	播放段落 Side Opposite $\begin{align*}45^\circ\end{align*}$ ::侧面45号对面____________________________________________________________	播放段落 Side Opposite $\begin{align*}90^\circ\end{align*}$ ::90号对面
1.	3
2.		7.2
3.			16
4.	$\begin{align*}5 \sqrt{2}\end{align*}$

播放段落

For 5-8, find the missing sides of the 30-60-90 triangle based on the information given in each row.
::对于5-8,根据每行提供的信息,找到30-60-90三角形的缺失侧。

播放段落 Problem Number ::问题编号	播放段落 Side Opposite $\begin{align*}30^\circ\end{align*}$ ::侧面对面30+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++	播放段落 Side Opposite $\begin{align*}60^\circ\end{align*}$ ::侧面对面60	播放段落 Side Opposite $\begin{align*}90^\circ\end{align*}$ ::90号对面
5.	$\begin{align*}3 \sqrt{2}\end{align*}$
6.		4
7.			15
8.			$\begin{align*}12 \sqrt{3}\end{align*}$

播放段落

Use the picture below for 9-11.
::9-11时请使用下图。

播放段落

9. Which angle corresponds to the side that is 12 units?
::9. 哪个角度与12个单位的侧面对应?

播放段落

10. Which side corresponds to the right angle?
::10. 哪一边与正确角度相对应?

播放段落

11. Which angle corresponds to the side that is 5 units?
::11. 哪个角度与5个单位的侧面对应?

播放段落

12. A right triangle has an angle of  $\begin{align*}\frac{\pi}{6}\end{align*}$ radians and a hypotenuse of 20 inches. What are the lengths of the other two sides of the triangle?
::12. 右三角形的角为 6 弧度,下限为 20 英寸,三角形其他两侧的长度是多少?

播放段落

13. A triangle has two angles that measure $\begin{align*}\frac{\pi}{4}\end{align*}$  radians. The longest side is 3 inches long. What are the lengths of the other two sides?
::13. 三角形有两个角度,可以测量 4 弧度,最长的边长3 英寸,其他两边的长度是多少?

播放段落

For 14-19, verify the Pythagorean Number Triple using the Pythagorean Theorem.
::14-19,使用Pytagoren理论来验证Pytagoren数字三号。

14. 3, 4, 5

15. 5, 12, 13

16. 7, 24, 25

17. 8, 15, 17

18. 9, 40, 41

19. 6, 8, 10

播放段落

20. Find another Pythagorean Number Triple using the method explained for finding “11, 60, 61”.
::20. 使用为找到 " 11、60、61 " 所解释的方法,再寻找一个 " 毕达哥林 " 数字三号。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。