Section: 代数基本理论 | 11.1 代数基本理论

Section outline

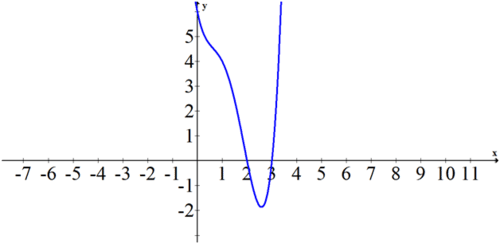
You have learned that a quadratic has at most two real zeroes and a cubic has at most three real zeros . You may have noticed that the number of real zeros is always less than or equal to the degree of the polynomial . By looking at a graph you can see when a parabola crosses the $\begin{aligned} x \end{aligned}$ axis 0, 1 or 2 times, but what does this have to do with ?
::您已经知道一个二次曲线最多有两个实际零位数, 一个立方体最多有三个实际零位数。您可能已经注意到, 实际零位数总是小于或等于多元度。通过查看一个图表, 您可以看到当抛物线过轴 0、 1 或 2 倍时, 这有什么关系 ?

The Fundamental Theorem of Algebra
::代数基本理论

A real number is any rational or irrational number. When a real number is squared, it will always produce a non-negative value. Complex numbers include real numbers and another type of number called . Unlike real numbers, imaginary numbers may produce a negative value when squared. The square root of negative one is defined to be the imaginary number $\begin{aligned} i \end{aligned}$ .
::一个实际数字是任何合理或不合理的数字。当一个实际数字被平方时,它总是产生一个非负值。复杂的数字包括实际数字和另一个称为数字的类型。与实际数字不同,想象数字在平方时可能产生负值。负数的平方根定义为虚数i。

$\begin{aligned} i = \sqrt{- 1} \end{aligned}$ and $\begin{aligned} i^{2} = - 1 \end{aligned}$
::i1和i21

Complex numbers are written with a real component and an imaginary component. All complex numbers can be written in the form $\begin{aligned} a + b i \end{aligned}$ . When the imaginary component is zero, the number is simply a real number. This means that real numbers are a subset of complex numbers.
::复杂数字是用一个真实的组件和一个假想的组件写入的。所有复杂数字都可以以 a+B 格式写入。当想象的组件为零时,数字只是一个真实的数字。这意味着真实数字是复杂数字的一个子集。

The Fundamental Theorem of Algebra states that an $\begin{aligned} n^{t h} \end{aligned}$ degree polynomial with real or complex coefficients has, with multiplicity, exactly $\begin{aligned} n \end{aligned}$ complex roots. This means a cubic will have exactly 3 roots, some of which may be complex.
::代数的基本理论指出,具有实际或复杂系数的 nth 度多元系数具有多重性,其根部十分复杂。这意味着一个立方体将完全有3 根,其中部分可能是复杂的。

Take the following polynomial.
::采取以下多边协议。

$\begin{aligned} f (x) = x^{2} + 9 \end{aligned}$
:xx)=x2+9

At first you may think that this does not have any roots but the Fundamental Theorem of Algebra states that it must have 2 roots. Both roots for this polynomial are complex.
::首先,你可能认为这没有根,但代数的基本理论指出它必须有两个根。这个多元的根是复杂的。

To find the roots for this complex polynomial, set $\begin{aligned} y = 0 \end{aligned}$ and solve for $\begin{aligned} x \end{aligned}$ . This will give you the two zeros.
::要找到这个复杂的多元数的根, 请设置 y=0 并解析 x。这将给您两个零。

\begin{aligned} 0 & = x^{2} + 9 \\ - 9 & = x^{2} \\ \pm 3 i & = x \end{aligned}

::0=x2+9-9=x23i=x

Thus the linear factorization of the function is:
::因此,该函数的线性因子化是:

$\begin{aligned} f (x) = (x - 3 i) (x + 3 i) \end{aligned}$
:xx)=(x-3i)(x+3i)

Multiplicity refers to when a root counts more than once. For example, in the following function the only root occurs at $\begin{aligned} x = 3 \end{aligned}$ .
::多重是指根数数不止一次。例如,在以下函数中,唯一的根数出现在 x=3 时。

$\begin{aligned} f (x) = (x - 3)^{2} \end{aligned}$
:xx)=(x-3)2

The Fundamental Theorem of Algebra states that this $\begin{aligned} 2^{n d} \end{aligned}$ degree polynomial must have exactly 2 roots with multiplicity. This means that the root $\begin{aligned} x = 3 \end{aligned}$ has multiplicity 2. One way to determine the multiplicity is to simply look at the degree of each of the factors in the factorized polynomial.
::代数的基本理论指出, 这个 2 度多元性必须完全有 2 根多重。这意味着根 x = 3 有多重。确定多重的方法之一是简单地查看参数化多元性中每项因素的程度。

$\begin{aligned} g (x) = (x - 1) (x - 3)^{4} (x + 2) \end{aligned}$
::g(x) = (x- 1) (x-3) 4(x+2)

This function has 6 roots. The first two roots $\begin{aligned} x = 1 \end{aligned}$ and $\begin{aligned} x = - 2 \end{aligned}$ have multiplicities of 1 because the power of each of their binomial factors is 1. The third root $\begin{aligned} x = 3 \end{aligned}$ has a multiplicity of 4 because the power of its binomial factor is 4. Keep in mind that all can be written in factorized form like the above polynomial, due to a theorem called the Linear Factorization Theorem.
::此函数有 6 根。前两个根 x=1 和 x2 的多重性为 1 , 因为它们的二进制因子的功率为 1 。第三根 x=3 的功率为 4 。因为它的二进制因子的功率为 4 。请记住, 所有的功率都可以以上述多义的形式写成, 因为一个叫做线性分解定理理论。

Examples
::实例

Example 1
::例1

Earlier, you were asked about the graphs of and their relationships to the zeroes of the parabolas. When a parabola fails to cross the $\begin{aligned} x \end{aligned}$ axis it still has 2 roots. These two roots happen to be imaginary numbers. The function $\begin{aligned} f (x) = x^{2} + 4 \end{aligned}$ does not cross the $\begin{aligned} x \end{aligned}$ axis, but its roots are $\begin{aligned} x = \pm 2 i \end{aligned}$ .
::早些时候,有人询问您有关抛物线的图形及其与无的点的关系。当抛物线无法跨过 x 轴时,它仍然有两个根。这两个根碰巧是想象数字。函数 f( x) =x2+4 没有跨过 x 轴, 但其根是 x2i 。

Example 2
::例2

Identify the polynomial that has the following five roots. $\begin{aligned} x = 0, 2, 3, \pm \sqrt{5} i \end{aligned}$
::识别具有以下五个根的多圆形。 x= 0, 2, 3, 5 i

Write the function in factorized form.
::以因素化形式写入函数。

$\begin{aligned} f (x) = (x - 0) (x - 2) (x - 3) (x - \sqrt{5} i) (x + \sqrt{5} i) \end{aligned}$
:xx) = (x-0) (x-2) (x-3) (x-5i) (x+5i)

When you multiply through, it will be helpful to do the complex conjugates first. Remember that Complex conjugates are pairs of complex numbers with real parts that are identical and imaginary parts that are of equal magnitude but opposite signs. The complex conjugates in this equation are $\begin{aligned} (x - \sqrt{5} i) (x + \sqrt{5} i) \end{aligned}$ .
::当您乘过时, 先进行复杂的共产体将很有帮助。记住, 复杂的共产体是复杂数字的组合体, 其真实部分是相同和想象的, 其大小相同, 但信号相反。此方程式的复杂共产体是 (x-5i) (x+5i) 。

\begin{aligned} f (x) & = x (x^{2} - 5 x + 6) (x^{2} - 5 \cdot (- 1)) \\ f (x) & = (x^{3} - 5 x^{2} + 6 x) (x^{2} + 5) \\ f (x) & = x^{5} - 5 x^{4} + 6 x^{3} + 5 x^{3} - 25 x^{2} + 30 x \\ f (x) & = x^{5} - 5 x^{4} + 11 x^{3} - 25 x^{2} + 30 x \end{aligned}

::f(x)=x5x4x6x3+6x3+5x3+5x3+5x3+5x3+5x3+5x3+5x3+5x3x3+5x3x3x2+30xf(x)=x5-5x4+113x3-252+30xxxx

Example 3
::例3

Write the polynomial that has the following roots: 4 (with multiplicity 3), 2 (with multiplicity 2) and 0.
::写下具有以下根源的多义: 4 (多重3), 2 (多重2) 和 0。

$\begin{aligned} f (x) = (x - 4)^{3} \cdot (x - 2)^{2} \cdot x \end{aligned}$
:xx) = (x-4) 3(x-2) 2x

Example 4
::例4

Factor the following polynomial into its linear factorization and state all of its roots.
::将以下多数值乘以线性因子化,并列出其全部根部。

$\begin{aligned} f (x) = x^{4} - 5 x^{3} + 7 x^{2} - 5 x + 6 \end{aligned}$
:x) =x4 - 5x3+7x2 - 5x+6

You can use polynomial long division to obtain the following factorization.
::您可以使用多数值长的分隔法获得以下乘数。

$\begin{aligned} f (x) = (x - 3) (x - 2) (x - i) (x + i) \end{aligned}$
:xx) = (x-3) (x-2) (x-i) (x+i)

If you need a place to start, it is helpful to look at the graph of the polynomial and notice that the graph shows you exactly where the real roots appear.
::如果您需要一个起始点, 查看多面形图是很有帮助的, 并注意该图显示您真实的根的位置。

Example 5
::例5

Can you create a polynomial with real coefficients that has one imaginary root? Why or why not?
::您能否用真实的系数来创建一个包含一个假想根的多元系数? 为什么或为什么?

No, if a polynomial has real coefficients then either it has no imaginary roots, or the imaginary roots come in pairs of complex conjugates (so that the imaginary portions cancel out when the factors are multiplied).
::不,如果一个多种族的系数是真实的,那么它要么没有想象中的根,要么想象中的根是复杂的共产物组合成的(这样当因素成倍增加时,想象中的部分就会取消)。

Summary

Imaginary numbers , denoted by $\begin{aligned} i, \end{aligned}$ may produce a negative number when squared.
$\begin{aligned} i = \sqrt{- 1} \end{aligned}$ and $\begin{aligned} i^{2} = - 1. \end{aligned}$
::i 表示的想象数字在正方形 i1 和 i21 时可能会产生负数。

Complex numbers include real numbers and imaginary numbers.
::复杂数字包括实际数字和想象数字。

All complex numbers can be written in the form $\begin{aligned} a + b i, \end{aligned}$ where a is the real component and $\begin{aligned} b \end{aligned}$ is the imaginary component.
::所有复数都可以以 a+B 格式写成,其中a 是真实的元件,b 是假想的元件。

The Fundamental Theorem of Algebra states that an $\begin{aligned} n^{t h} \end{aligned}$ degree polynomial with real or complex coefficients has, with multiplicity, exactly $\begin{aligned} n \end{aligned}$ complex roots.
::代数的基本理论指出,具有实际或复杂系数的 nth 度多元系数具有多重性,其根部十分复杂。

Multiplicity refers to when a root counts more than once, and can be determined by looking at the degree of each factor in the factored polynomial.
::多重性是指根数不止一次时,并且可以通过考虑因素多元体中每个因素的程度来确定。

Review
::回顾

For 1 - 4, find the polynomial with the given roots.
::1 - 4, 找到与给定根的多种族关系。

1. 2 (with multiplicity 2), 4 (with multiplicity 3), $\begin{aligned} 1, \sqrt{2} i, - \sqrt{2} i \end{aligned}$ .
::1. 2,2,4(3),1,2i,-2i。

2. 1, -3 (with multiplicity 3), $\begin{aligned} - 1, \sqrt{3} i, - \sqrt{3} i \end{aligned}$
::2. 1-3(多重3),-1-3i,-3i

3. 5 (with multiplicity 2), -1 (with multiplicity 2), $\begin{aligned} 2 i, - 2 i \end{aligned}$
::3. 5(多重2),-1(多重2),2i,-2i

4. $\begin{aligned} i, - i, \sqrt{2} i, - \sqrt{2} i \end{aligned}$
::4. i,i,2i,-2i

For each polynomial, factor into its linear factorization and state all of its roots.
::对于每个多面体,将系数纳入线性乘数,并阐明其全部根源。

5. $\begin{aligned} f (x) = x^{5} + 4 x^{4} - 2 x^{3} - 14 x^{2} - 3 x - 18 \end{aligned}$
::5. f(x)=x5+4x4-2x3-14x2-3x-18

6. $\begin{aligned} g (x) = x^{4} - 1 \end{aligned}$
::6. g(x)=x4-1

7. $\begin{aligned} h (x) = x^{6} - 12 x^{5} + 61 x^{4} - 204 x^{3} + 532 x^{2} - 864 x + 576 \end{aligned}$
::7. h(x)=x6-12x5+61x4-204x3+532x2-864x+576

8. $\begin{aligned} j (x) = x^{7} - 11 x^{6} + 49 x^{5} - 123 x^{4} + 219 x^{3} - 297 x^{2} + 243 x - 81 \end{aligned}$
::8. j(x) =x7- 11x6+49x5 - 123x4+219x3-297x2+243x- 81

9. $\begin{aligned} k (x) = x^{5} + 3 x^{4} - 11 x^{3} - 15 x^{2} + 46 x - 24 \end{aligned}$
::9. k(x) =x5+3x4- 11x3- 15x2+46x-24

10. $\begin{aligned} m (x) = x^{6} - 12 x^{4} + 23 x^{2} + 36 \end{aligned}$
::10.(x)=x6-12x4+23x2+36

11. $\begin{aligned} n (x) = x^{6} - 3 x^{5} - 10 x^{4} - 32 x^{3} - 81 x^{2} - 85 x - 30 \end{aligned}$
::11. n(x)=x6-3x5-10x4-32-81x2-85x-30

12. $\begin{aligned} p (x) = x^{6} + 4 x^{5} + 7 x^{4} + 12 x^{3} - 16 x^{2} - 112 x - 112 \end{aligned}$
::12.p(x)=x6+4x5+7x4+12x3-16x2-112x-112

13. How can you tell the number of roots that a polynomial has from its equation?
::13. 你如何从多元等式中分辨出根数?

14. Explain the meaning of the term “multiplicity”.
::14. 解释 " 多重 " 一词的含义。

15. A polynomial with real coefficients has one root that is $\begin{aligned} \sqrt{3} i \end{aligned}$ . What other root(s) must the polynomial have?
::15. 具有实际系数的多元系数有一个根根是3i。该多元系数还必须有其他根吗?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

The Fundamental Theorem of Algebra ::代数基本理论

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)