Section: 负声明 | 16.3 否定性发言

Section outline

In everyday speech, negative statements are often ambiguous or unclear. Mathematically, you need a precise way to negate statements so that you can accurately determine whether statements are true or false. When is the negation of the following sentence true?
::在日常演讲中,负面言论往往含糊不清或含糊不清。从数学角度讲,你需要精确的方法来否定这些言论,以便准确确定这些言论是真实还是虚假。何时否定以下一句是真实的?

If I am not cold then it is not snowing.
::如果我不冷,那它就不会下雪。

Nega tions
::内括号

While in everyday language the opposite of “dog” might be “cat”, in mathematics the opposite of “dog” is “not a dog”. Using the word “not” is the basic way to negate an atomic sentence. An atomic sentence is a logical statement without logical connectives that has a truth value .
::在日常语言中,“狗”的反义词可能是“猫”,而在数学中,“狗”的反义词是“不是狗”,使用“不”一词是否定原句的基本方式,原子句是逻辑的表述,没有具有真理价值的逻辑联系。

Original sentence $\begin{aligned} (D) \end{aligned}$ : That thing is a dog .
::原句(D):那东西是只狗。

Negation of sentence $\begin{aligned} (\sim D) \end{aligned}$ : That thing is not a dog .
::判决无效(QQD):那东西不是狗。

The box below represents the universe of all things. This universe can be separated into things that are dogs and things that are not dogs.
::下面的框代表着所有事物的宇宙。这个宇宙可以被分离成狗的东西, 而不是狗的东西。

To negate complex statements that involve logical connectives like or, and, or if-then, you should start by constructing a truth table and noting that negation completely switches the truth value.
::否定涉及逻辑联系的复杂言论,比如,或者,或者,如果,那么,你应该首先构建一个真相表,指出否定完全改变真相的价值。

The negation of a conditional statement is only true when the original if-then statement is false.
::只有在原先的如果当时的声明是虚假的时,才否定有条件的声明。

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} P \to Q \end{aligned}$	$\begin{aligned} \sim (P \to Q) \end{aligned}$
T	T	T	F
T	F	F	T
F	T	T	F
F	F	T	F

The negation of a conjunction is only false when the original two statements are both true. A conjunction is two statements that are joined by an "and".
::如果最初的两种说法都属实,则否定合并的说法是虚假的。合并的意思是两种配有“和”的说法。

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} P \land Q \end{aligned}$	$\begin{aligned} \sim (P \land Q) \end{aligned}$
T	T	T	F
T	F	F	T
F	T	F	T
F	F	F	T

The negation of a disjunction is only true when both of the original statements are false. A disjunction is two statements that are joined by an "or".
::只有在两个原始声明都是虚假的时,才能否定脱节。脱节是指两个声明,加上一个“或”加在一起。

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} P \lor Q \end{aligned}$	$\begin{aligned} \sim (P \lor Q) \end{aligned}$
T	T	T	F
T	F	T	F
F	T	T	F
F	F	F	T

Set theory circles can also be used to interpret the negation of a disjunction or a conjunction.
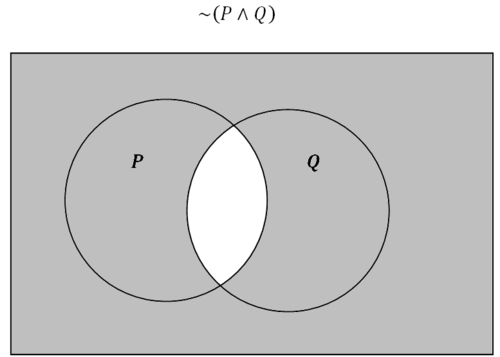
::设置理论圈也可以用来解释对脱离或结合的否定。

The shaded portion in the box represents the area that is within $\begin{aligned} P \end{aligned}$ or within $\begin{aligned} Q \end{aligned}$ . Recall that in mathematical logic, this is written as $\begin{aligned} P \lor Q \end{aligned}$ . In set theory this area is represented similarly as $\begin{aligned} P \cup Q \end{aligned}$ where the symbol $\begin{aligned} \cup \end{aligned}$ stands for union. While the notation is slightly different, the reasoning about the relationships and implications is identical.
::框中的阴影部分代表 P 或 Q 内的区域。回顾在数学逻辑中,这是写成的 P 。在设定的理论中, 这个区域与 P 相似, 符号 { { 表示结合。虽然符号略微不同, 但关于关系和含义的推理是一样的。

When you negate the statement, you completely switch what is shaded.
::当你否定声明时,你完全换掉阴影。

A different way to think about this shaded region is that it is the region that is not in $\begin{aligned} P \end{aligned}$ and also not in $\begin{aligned} Q \end{aligned}$ . This means that $\begin{aligned} \sim (P \lor Q) \end{aligned}$ is equivalent to $\begin{aligned} \sim P \land \sim Q \end{aligned}$ .
::对于这个阴暗区域,另一种不同的思考方式是,不是在P区,也不是在Q区。这意味着(P)相当于P。

$\begin{aligned} \sim (P \lor Q) \Leftrightarrow \sim P \land \sim Q \end{aligned}$
::~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

The symbol “ $\begin{aligned} \Leftrightarrow \end{aligned}$ ” works in mathematical logic and set theory the same way “ $\begin{aligned} = \end{aligned}$ ” works in arithmetic and algebra. In this case, the negative appears to distribute throughout the or statement by negating each statement individually and changes the or statement to an and statement. This is called De Morgan’s Law .
::在数学逻辑中,符号“”在数学逻辑中起作用,并将理论与算术和代数法中的“=”一样设定为“=”法。在这种情况下,负值似乎通过逐个否定每个语句和将语句或语句改为一个和语句而在整个语句中分布。这被称为“德摩根法 ” ( De Morgan Law ) 。

Negating a conjunction gives a similar result.
::排除结合也得出了类似的结果。

The shaded portion in the box represents the area that is within $\begin{aligned} P \end{aligned}$ and within $\begin{aligned} Q \end{aligned}$ . In mathematical logic this is written as $\begin{aligned} P \land Q \end{aligned}$ . In set theory this area is represented similarly as $\begin{aligned} P \cap Q \end{aligned}$ where the symbol $\begin{aligned} \cap \end{aligned}$ stands for intersection . As before, the notation between mathematical logic and set theory is slightly different. However, the reasoning about the relationships and the logical implications are identical.
::框中的阴影部分代表 P 和 Q 内的区域。在数学逻辑中, 这个区域是写成为 P 。在设定的理论中, 这个区域与 P 相似, 符号 { { { 表示交叉点。和以前一样, 数学逻辑和设定理论之间的符号略有不同。但是, 关系和逻辑含义的推理是相同的。

When you negate the statement, you completely switch what is shaded.
::当你否定声明时,你完全换掉阴影。

A different way to think about this shaded region is to consider that it represents everything that isn’t in $\begin{aligned} P \end{aligned}$ or isn’t in $\begin{aligned} Q \end{aligned}$ .
::思考这个阴暗区域的不同方式是, 认为它代表着一切非P或Q的事物。

$\begin{aligned} \sim (P \land Q) \Leftrightarrow \sim P \lor \sim Q \end{aligned}$
::~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

This is a second representation of De Morgan’s Law.
::这是De Morgan法律的第二个代表。

As mathematical sentences become more complex with additional connectives, and set theory circles are good ways to interpret when the statements are true and when the statements are false.
::随着数学句子随着额外的连结而变得更加复杂,并且设定理论圈是当声明属实和声明属虚假时解释这些说法的好方法。

Examples
::实例

Example 1
::例1

Earlier, you were asked when the negation of the following statement is true.
::早些时候,有人问你,否认以下声明是何时发生的。

If I am not cold, then it is not snowing.
::如果我不冷,那它就不会下雪。

The statement already has several negative parts, so it is incorrect to simply switch one or both of the negations.
::这种说法已经有几个负面部分,因此,简单地转换一种或两种否定说法是不正确的。

$\begin{aligned} P = I a m c o l d \end{aligned}$ .
::P=我很冷。 (P=P=P=P=P=P=P=P=P=P=P=P=P=P=P=P=PL=P=P=PL=PL=PL=PL=PL=PL=PL=PL=PL=PL=PL=PL=P=PL=P=P=P=P=我冷冷。

$\begin{aligned} Q = I t i s s n o w i n g \end{aligned}$ .
::下雪了下雪了下雪了下雪了下雪了下雪了下雪了下雪了

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} \sim P \end{aligned}$	$\begin{aligned} \sim Q \end{aligned}$	$\begin{aligned} \sim P \to \sim Q \end{aligned}$	$\begin{aligned} \sim (\sim P \to \sim Q) \end{aligned}$
T	T	F	F	T	F
T	F	F	T	T	F
F	T	T	F	F	T
F	F	T	T	T	F

Start by building up to the original statement. Then, add a column that completely negates the original statement. Notice that there is only one row where the final negated statement is true. That is when $\begin{aligned} P \end{aligned}$ is false and $\begin{aligned} Q \end{aligned}$ is true. Therefore, the negation of the original sentence is true when “I am not cold” and “it is snowing”.
::开始添加原始语句。然后, 添加一列完全否定原始语句。注意只有一行最后否定语句是真实的。也就是说, P 是虚假的, Q 是真实的。因此, “ 我不冷” 和“ 下雪 ” 对原句的否定是真实的。

Example 2
::例2

Use set theory circles to interpret the negation of a conditional statement and explain how the negation of a conditional can be written in a different way.
::使用设定理论圈来解释对有条件声明的否定,并解释对有条件声明的否定如何以不同方式写成。

The shaded portion in the box represents the area that makes the following statement true.
::框中的阴影部分代表使以下语句真实化的区域。

Notice that there are four different regions in the Venn Diagram which correspond to the four different rows of the conditional truth table. The only space that does not make the statement true is when $\begin{aligned} P \end{aligned}$ is true (inside circle $\begin{aligned} P \end{aligned}$ ) and $\begin{aligned} Q \end{aligned}$ is false (outside circle $\begin{aligned} Q \end{aligned}$ ).
::请注意, Venn 图表中有四个不同的区域, 与有条件的真相表格的四个不同行相对应。唯一不使声明真实的空格是 P 是真实的( 在 P 圈内) 和 Q 是虚假的( 在 Q 圈外 ) 。

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} P \to Q \end{aligned}$
T	T	T
T	F	F
F	T	T
F	F	T

To negate this statement, you switch the values in the truth table and switch the shaded region in the Venn Diagram.
::要否定此语句, 您将转换真实表格中的值, 并切换 Venn 图表中的阴影区域。

A different way to think about this shaded region is to see it as the space that is in $\begin{aligned} P \end{aligned}$ but not in $\begin{aligned} Q \end{aligned}$ .
::思考这个阴暗区域的不同方式是将它视为在P的空间,而不是在Q的空间。

$\begin{aligned} \sim (P \to Q) \Leftrightarrow P \land \sim Q \end{aligned}$
::~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~

Example 3
::例3

Show that the following statements are equivalent in a truth table. The symbol ≡ means equivalent. To be equivalent in this case means to be true at the same time and false at the same time.
::显示下列语句在真实表格中等同。符号 = * 表示等同。在此情况下等同意味着同时真实, 同时虚假。

$\begin{aligned} P \land Q \equiv \sim (\sim P \lor \sim Q) \end{aligned}$
::

While a truth table is not a proof, it can help you recognize when two statements have the same truth values.
::虽然真相表不是证据,但当两个声明具有相同的真相价值时,它可以帮助你认识真相表。

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} \sim P \end{aligned}$	$\begin{aligned} \sim Q \end{aligned}$	$\begin{aligned} \sim P \lor \sim Q \end{aligned}$	$\begin{aligned} \sim (\sim P \lor \sim Q) \end{aligned}$	$\begin{aligned} P \land Q \end{aligned}$
T	T	F	F	F	T	T
T	F	F	T	T	F	F
F	T	T	F	T	F	F
F	F	T	T	T	F	F

Notice that the final two columns are identical.
::请注意最后两栏相同。

Example 4
::例4

Write a sentence in two different ways illustrating the mathematical statement in Example 3
::以两种不同方式写一个句子,说明例3中的数学语句

$\begin{aligned} P \land Q \end{aligned}$ : I like movies and I like TV. $\begin{aligned} \sim (\sim P \lor \sim Q) \end{aligned}$ : It is not the case that either I don’t like movies or I don’t like TV.
::」:我喜欢电影, 我喜欢电视。 (P):我不喜欢电影或不喜欢电视,

Example 5
::例5

A tautology is a logical statement that is always true. Demonstrate the following tautology in a truth table.
::美容学是一个合乎逻辑的陈述,它永远是真实的。在真实的表格中展示以下的同义词。

$\begin{aligned} B \to (A \lor \sim A) \end{aligned}$
::B_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} A \end{aligned}$	$\begin{aligned} \sim A \end{aligned}$	$\begin{aligned} B \end{aligned}$	$\begin{aligned} A \lor \sim A \end{aligned}$	$\begin{aligned} B \to (A \lor \sim A) \end{aligned}$
T	F	F	T	T
T	F	T	T	T
F	T	T	T	T
F	T	F	T	T

Notice that the last column is all T's. This means that this statement is always true and therefore is a tautology.
::注意最后一栏是所有 T 。这意味着这个声明永远是真实的, 因此是一个同义词。

Summary

Negating atomic sentences involves using the word "not" or “ $\begin{aligned} \sim \end{aligned}$ ” to switch the truth value of the statement.
::否定原子句意味着使用“不”或“``'”一词来改变声明的真相价值。

Negating complex statements with logical connectives requires constructing a truth table and noting the switch in truth values.
::否定具有逻辑联系的复杂陈述,需要构建一个真相表,注意到真相价值的转变。

$\begin{aligned} P \cup U \end{aligned}$ represents union of P and Q, which is the area that is within either P or Q
::PU代表P和Q的联盟,这是在P或Q之内的地区。

$\begin{aligned} P \cap U \end{aligned}$ represents the intersection of P and Q which is the area that is within both P and Q
::PU代表P和Q的交叉点,即P和Q之间的区域。

De Morgan's Law describes how a negation works over conjunctions:
- $\begin{aligned} \sim (P \lor Q) \Leftrightarrow\sim P \land \sim Q \end{aligned}$
  ::~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~
- $\begin{aligned} \sim (P \land Q) \Leftrightarrow\sim P \lor \sim Q \end{aligned}$
  ::~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ (P) ~ ~ ~ ~ ~ ~ ~ ~ ~
::De Morgan的法律描述否定的结合是如何运作的: (P)(P)(P)(P)(P)(P)(P)(P)(P)(P)(P)(

Review
::回顾

I’m either going to go skiing or snowboarding next weekend.
::我要么去滑雪, 要么下周末去滑雪。

1. Identify the atomic statements in the above sentence and use logical connectives to rewrite the sentence with symbols.
::1. 标明上述句子中的原子语句,并使用逻辑连接来用符号重写句子。

2. Write the negation of the sentence with symbols and write the negation of the sentence in words in a natural way.
::2. 用符号书写否定句子的文字,用自然的语言书写否定句子的文字。

Mike and John both ate lunch with me.
::麦克和约翰都和我一起吃午饭

3. Identify the atomic statements in the above sentence and use logical connectives to rewrite the sentence with symbols.
::3. 标明上述句子中的原子语句,并使用逻辑连接来用符号重写句子。

4. Write the negation of the sentence with symbols and write the negation of the sentence in words in a natural way.
::4. 用符号书写句子的否定,用自然的文字书写句子的否定。

Neither my brother nor my sister wants to play with me.
::我哥哥和妹妹都不想跟我玩

5. Identify the atomic statements in the above sentence and use logical connectives to rewrite the sentence with symbols.
::5. 标明上述句子中的原子语句,并使用逻辑连接来用符号重写句子。

6. Write the negation of the sentence with symbols and write the negation of the sentence in words in a natural way.
::6. 用符号书写句子的否定,用自然的文字书写句子的否定。

Write negations for the following statements.
::为以下声明写作否定。

7. All dogs go to heaven.
::7. 所有狗都上天堂。

8. My teacher is seldom wrong.
::8. 我的老师很少说错话。

9. Everyone likes pizza.
::9. 每个人都喜欢比萨饼。

Make truth tables for each of the following.
::为以下各点绘制真相表格。

10. $\begin{aligned} (P \land Q) \lor \sim Q \end{aligned}$
::10. (P)_________________________________________________________________________________________________________________________________

11. $\begin{aligned} P \land (Q \lor \sim Q) \end{aligned}$
::11. P____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

12. $\begin{aligned} (P \lor Q) \lor \sim R \end{aligned}$
::12. (P)_______________________________________________________________________________________________________________________________________________________________________________________________________

13. $\begin{aligned} (\sim P \land \sim Q) \lor \sim R \end{aligned}$
::13. (

14. What is the simplest statement that is equivalent to #11: $\begin{aligned} P \land (Q \lor \sim Q) \end{aligned}$ ?
::14. 最简单的说明是什么,相当于 #11:P()?

15. Use De Morgan’s Law to find a statement equivalent to the following statement: $\begin{aligned} \sim (Q \lor \sim Q) \end{aligned}$
::15. 利用德摩根法律找到相当于以下声明的声明:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

16. Use De Morgan’s Law to find a statement equivalent to the following statement: $\begin{aligned} \sim (P \lor Q) \lor \sim R \end{aligned}$
::16. 利用德摩根法律找到相当于以下声明的声明:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Nega tions ::内括号

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)