偶函数和奇函数

播放段落

While looking at the equation of a function that needed to be graphed for homework, a student recognized that the task would go quickly because the sign of the values in the domain did not matter in calculating the function values, and only half the values in the domain needed to be used. What kind of function was the student evaluating?
::一位学生在查看需要为家庭作业绘制图表的函数方程式时承认,任务会很快完成,因为在计算函数值时,域内数值的标志并不重要,只有域内值的一半需要使用。 学生们评估的功能是什么?

播放段落

Types of Functions: Even, Odd, or Neither
::函数类型:偶数、偶数或偶数或偶数

播放段落

A function  $\begin{array}{r}f(x)\end{array}$ is an even function if: $\begin{array}{r}f(x)=f(-x)\end{array}$ , i.e., the value of the function acting on an argument  $\begin{array}{r}x\end{array}$ is the same as the value of the function when acting on the argument $\begin{array}{r}-x\end{array}$ .  So, for example, if  $\begin{array}{r}f(x)\end{array}$ is an even function, then  $\begin{array}{r}f(2)\end{array}$ has the same answer as $\begin{array}{r}f(-2)\end{array}$ ;  $\begin{array}{r}f(5)\end{array}$ has the same answer as $\begin{array}{r}f(-5)\end{array}$ , and so on.
::函数 f( x) 是一个偶数函数, 如果 : f( x) = f( - x) , 则函数 f( x) 是一个偶数函数, 即根据参数 x 行事的函数值与根据参数 - x 行事的函数值相同。 因此, 例如, 如果 f( x) 是偶数函数, 那么f(2) 的答案与 f( - 2) 相同; f (5) 的答案与 f( - 5) 等相同。

播放段落

Even functions are symmetric about the $\begin{array}{r}y\end{array}$ -axis.
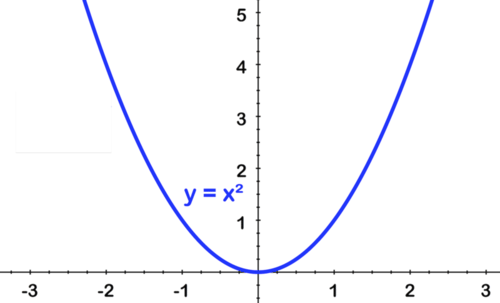
::甚至函数也与 Y 轴对称。

播放段落

To show that a function is even, show that the definition  $\begin{array}{r}f(x)=f(-x)\end{array}$  holds. Take the function  $\begin{array}{r}y=f(x)=x^2\end{array}$  .
::要显示函数是偶数,请显示定义 f( x) =f( - x) 持有。 执行 y=f( x) =x2 函数 。

播放段落

$\begin{array}{r}f(-x)=(-x{)}^2=x^2=f(x)\end{array}$ . So the function is an even function. The function graph below shows that the function is symmetric with respect to the $\begin{array}{r}y\end{array}$ -axis.
::f( x) = (- x) 2=x2=x2=f( x) 。 所以函数是一个偶数函数。 下面的函数图显示该函数相对于 y 轴是对的。

播放段落

In contrast to an even function, a function $\begin{array}{r}f(x)\end{array}$ is an odd function if: $\begin{array}{r}-f(x)=f(-x)\end{array}$ , i.e., the function is odd when the negative of the function's answer for a given argument is the same as the function acting on the negative argument. If a function  $\begin{array}{r}f(x)\end{array}$ were odd, then $\begin{array}{r}f(-2)=-f(2)\end{array}$ ; $\begin{array}{r}f(-5)=-f(5)\end{array}$ , and so on.
::与偶数函数相对,函数 f(x) 是一个奇怪的函数,如果: -f(x) =f(-x),即当函数对某一参数的答复的负数与对负参数的负数相同时,函数函数f(x) 是一个奇数。如果函数f(x) 是奇数,则函数f(x) =*f(2);f(-5) =*f(5) 等。

播放段落

Odd functions are not symmetric about the $\begin{array}{r}y\end{array}$ -axis, but they are symmetric about the origin.
::Odd 函数对 Y 轴不对称, 但对源代码对称 。

播放段落

To show that a function is odd, show that the definition  $\begin{array}{r}-f(x)=f(-x)\end{array}$  holds. Take the function  $\begin{array}{r}y=x^3\end{array}$
::要显示函数是奇数,请显示定义 -f( x) =f( x) 持有。使用函数 y=x3

播放段落

$\begin{array}{r}f(-x)=(-x{)}^3=-x^3=-f(x)\end{array}$ . So the function is an odd function.
::f(- x) = (- x) = (- x) = = =x) {x3}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以函数是一个奇函数 函数。

播放段落

It is important to remember that a function does not have to be even or odd . Most functions are neither even nor odd.
::重要的是要记住,函数不需要平衡或奇异。 大多数函数既不是偶数,也不是奇数。

播放段落

To determine whether the function $\begin{array}{r}y=3(x+2{)}^2+4\end{array}$  is even or odd, apply the test for both types.
::要确定 y=3(x+2)2+4 函数是偶数还是奇数, 请对两种类型都进行测试 。

播放段落

Apply the test for an even function: $\begin{array}{r}f(-x)=3(-x+2{)}^2+4=3(x-2{)}^2+4\ne f(x)\end{array}$ . The function is not an even function.
::对一个偶数函数应用测试 : f( - x)=3( - x+2) 2+4=3( x-2) 2+4*f( x) 。 该函数不是一个偶数函数 。

播放段落

Apply the test for an odd function: $\begin{array}{r}f(-x)=3(x-2{)}^2+4\ne -f(x)\end{array}$ . The function is not an odd function.
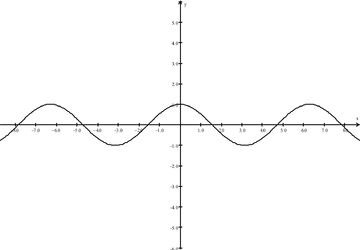
::应用一个奇函数的测试: f(- x)=3( x-2)2+4f( x)。该函数不是一个奇函数。

播放段落

The above function is neither even nor odd. As can be seen in the graph below, the function is neither symmetric about the $\begin{array}{r}y\end{array}$ -axis nor symmetric about the origin.
::上述函数既不是偶数也不是奇数,如下图所示,该函数既非对数y轴,也非对数源。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were told about a problem where the student only needed half of the values in the domain to graph his function because the signs did not matter.  Either all negative values or all positive values could be used to graph the function. To be able to graph a function without having to worry about the sign of values in the domain means that the function must be an even function,  $\begin{array}{r}f(x)=f(-x)\end{array}$ .  This means that t he graph is is symmetric about the $\begin{array}{r}y-axis\end{array}$  .
::早些时候,有人告诉您一个问题,即学生仅仅需要域内一半的值来显示其函数,因为符号无关紧要。要么所有负值,要么所有正值都可以用来显示函数。为了能够绘制函数,而不必担心域内数值的符号,这意味着函数必须是偶数函数, f(x)=f(x)-x。这意味着该图与它们-轴对称。

播放段落

Example 2
::例2

播放段落

Here are eight basic functions that are often encountered. Use their function graphs to determine whether they are even, odd, or neither.
::这是经常遇到的八个基本函数。 使用它们的函数图形来确定它们是否平坦、 奇异或两者都不是 。

播放段落
• $\begin{array}{r}Linear:f(x)=xDomain=AllrealsRange=Allreals\end{array}$
  
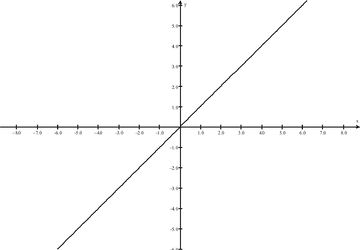
  ::线性 : f( x) = xDomain = 全部实值 = 所有实值

播放段落

This linear function is symmetric about the origin and is an odd function: $\begin{array}{r}f(x)=f(-x)\end{array}$ .
::此线性函数是源的对称函数, 是一个奇函数 : f( x) = f( - x) 。

播放段落
• $\begin{array}{r}Square(Quadratic)f(x)=x^{2}Domain=AllrealsRange=\{y\ge 0\}\end{array}$
  
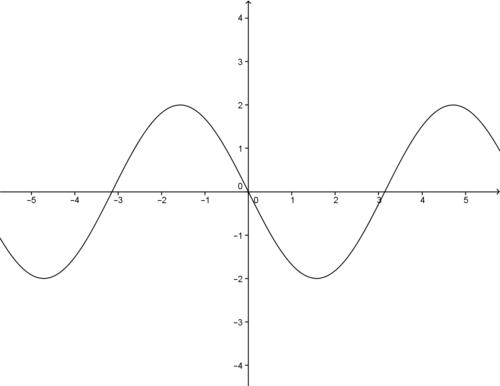
  ::平方( 二次曲线) f( x) =x2Domain = 全部正弦代表 {y_0}

播放段落

As shown earlier in the concept, this quadratic function is symmetric about the $\begin{array}{r}y\end{array}$ -axis and is an even function: $\begin{array}{r}f(x)=f(-x)\end{array}$ .
::如先前的概念所示,该二次函数与 Y 轴对齐,是一个偶数函数: f( x) = f( - x) 。

播放段落
• $\begin{array}{r}Cube(Polynomial)f(x)=x^{3}Domain=AllrealsRange=Allreals\end{array}$
  
  ::Cube( Polynomial) f(x) =x3Domain = 所有真实数字 = 所有真实数字

播放段落

As shown earlier in the concept, this cubic function is symmetric about the origin and is an odd function: $\begin{array}{r}f(-x)=-f(x)\end{array}$ .
::如先前的概念所示,此立方函数与源代码对称, 是一个奇函数 : f- x) f( x) 。

播放段落
• $\begin{array}{r}SquareRootf(x)=\sqrt{x}Domain=\{x\ge 0\}Range=\{y\ge 0\}\end{array}$
  
  ::平方根 f( x) =xDomain = {x=0} 兰格 = {y=0}

播放段落

This square root function is neither symmetric about the origin or the $\begin{array}{r}y\end{array}$ -axis, and is neither odd nor even.
::此平方根函数既不对称源或 Y 轴, 也不奇怪, 甚至不奇特 。

播放段落
• $\begin{array}{r}AbsoluteValuef(x)=|x|Domain=AllrealsRange=\{y\ge 0\}\end{array}$
  
  ::绝对值 f(x)\\\\\\\\\\\\\\Domain = 所有实值Range = {y=0}

播放段落

This absolute value function is symmetric about the $\begin{array}{r}y\end{array}$ -axis and is an even function: $\begin{array}{r}f(x)=f(-x)\end{array}$ .
::此绝对值函数与 Y 轴对称, 是一个偶函数 : f( x) = f( x) 。

播放段落
• $\begin{array}{r}Rationalf(x)=\frac{1}{x}Domain=\{x\ne 0\}Range=\{y\ne 0\}\end{array}$
  
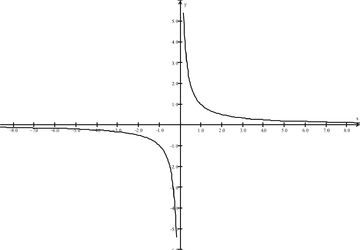
  ::有理 f( x) = 1xDomain = {x} 0} Range = {y} 0}

播放段落

This rational value function is symmetric about the origin and is an odd function: $\begin{array}{r}f(-x)=-f(x)\end{array}$ .
::此合理值函数与源值对称, 是一个奇数函数 : f- x)\\\\\\ f( x) 。

播放段落
• $\begin{array}{r}Sinef(x)=\sin xDomain=AllrealsRange=\{-1\le y\le 1\}\end{array}$
  
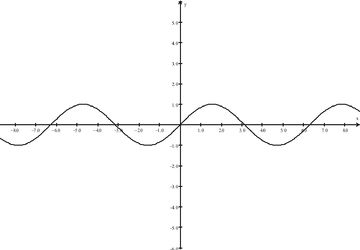
  ::Sine f(x) = sinxDomain = 所有实值Range = 1y1}

播放段落

This sine function is symmetric about the origin and is an odd function: $\begin{array}{r}f(-x)=-f(x)\end{array}$ .
::此正弦函数是源代码的对称, 是一个奇函数 : f -x)\\\\\ f( x) 。

播放段落
• $\begin{array}{r}Cosinef(x)=\cos xDomain=AllrealsRange=\{-1\le y\le 1\}\end{array}$
  
  ::余弦 f(x) = cosxDomain = 全部正弦 = 1y1}

播放段落

This sine function is symmetric about the $\begin{array}{r}y\end{array}$ -axis and is an even function: $\begin{array}{r}f(x)=f(-x)\end{array}$ .
::此正弦函数与 Y 轴对称, 是一个偶函数 : f( x) = f( x) 。

播放段落

Review
::回顾

播放段落

For #1-4, is the function even, odd, or neither?
::对于 # 1-4, 函数是偶数, 奇数, 还是两者都不是?

1. 
2. 
3. 
4. 

播放段落

For #5-15, determine algebraically whether the function is even, odd or neither.
::对于# 515, 确定代数, 函数是偶数、 奇数还是非偶数 。

播放段落
5. $\begin{array}{r}y=-4x\end{array}$
   ::y4x
播放段落
6. $\begin{array}{r}f(x)=2|x|+3\end{array}$
   :xx)=2x*3
播放段落
7. $\begin{array}{r}y=(x+3{)}^2-1\end{array}$
   ::y= (x+3) 2- 1
播放段落
8. $\begin{array}{r}h(x)=\frac{x^3-2x}{x^4+3x^2}\end{array}$
   ::h(x) =x3 - 2x24+3x2
播放段落
9. $\begin{array}{r}g(x)=1-x^5+x^{23}\end{array}$
   ::g(x) =1 - x5+x23
播放段落
10. $\begin{array}{r}k(x)=5x\sqrt{x^4-7x^2}\end{array}$
    : kx) = 5x24 - 7x2
播放段落
11. $\begin{array}{r}y=3{\sin }^2(x)-4\end{array}$
    ::y=3sin2(x)- 4
播放段落
12. $\begin{array}{r}h(x)=\frac{\sin x}{x}\end{array}$
    ::h(x) =sinxxx
播放段落
13. $\begin{array}{r}f(x)=\sqrt{|x|}\end{array}$
    :fx)
播放段落
14. $\begin{array}{r}f(x)=4\sqrt{|x-1|}\end{array}$
    :xx)=4x-1
播放段落
15. $\begin{array}{r}k(x)=(x+3)(x-4)\end{array}$
    : kx) = (x+3) (x- 4)

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。