节: 反逆三角函数 | 7.6 逆三角函数

章节大纲

You already know the six trigonometric functions and their relationships to the angles and sides of right triangles. But what if you were more interested in the angles themselves. Would you know how to find an angle given the value of a trigonometric function? If so, do you know
::您已经知道六个三角函数及其与右三角形角度和侧面的关系。但如果您对角度本身更感兴趣, 您是否知道如何找到一个角度, 以三角函数的价值为基准? 如果知道, 您是否知道。

Inverse Trigonometric Functions
::反逆三角函数

You already know the six trigonometric functions: $\begin{aligned} \sin x, \cos x, \tan x, \csc x, \sec x, \cot x \end{aligned}$ . But are their inverse trigonometric functions? The answer is yes, but some restrictions must be placed on the domain of each of the six functions before an inverse can be defined.
::您已经知道六个三角函数 : sinx,cosx,tanx,cscx,secx,cotx。但是它们的反三角函数是反三角函数吗? 答案是是肯定的, 但是在能够定义一个反函数之前, 必须对六个函数的每个函数的域域设置一些限制。

If we ask what is $\begin{aligned} \sin (\frac{π}{6}) \end{aligned}$ equal to, the answer is $\begin{aligned} \frac{1}{2} \end{aligned}$ . That is simple enough. But what if we ask what angle has a sine of $\begin{aligned} \frac{1}{2} \end{aligned}$ ? The inverse trigonometric function gives the answer. So we say $\begin{aligned} \sin (\frac{π}{6}) = (\frac{1}{2}) \end{aligned}$ , but $\begin{aligned} \sin^{- 1} (\frac{1}{2}) = (\frac{π}{6}) \end{aligned}$ . Note that the output of the inverse is in units of radians, not degrees. The “ $\begin{aligned} \sin^{- 1} \end{aligned}$ ” is the notation for the inverse of the sine function. For every one of the six trigonometric functions there is an associated inverse function. They are denoted as follows:
::如果我们问什么是罪,答案是12。这非常简单。但如果我们问什么角度的正弦是12?反三角函数提供了答案。所以我们说sin(6)=(12),但说sin-1(12)=(6)。请注意,反的输出是弧度的单位,而不是度。“sin-1”是正弦函数的反义符号。对于六个三角函数中的每一函数,都有一个相关的反函数。这些函数的注意如下:

Trigonometric function/inverse pairs
$\begin{aligned} \sin x \leftrightarrow \sin^{- 1} x \equiv \arcsin x \end{aligned}$	$\begin{aligned} \csc x \leftrightarrow \csc^{- 1} x \equiv arccsc x \end{aligned}$
$\begin{aligned} \cos x \leftrightarrow \cos^{- 1} x \equiv \arccos x \end{aligned}$	$\begin{aligned} \sec x \leftrightarrow \sec^{- 1} x \equiv arcsec x \end{aligned}$
$\begin{aligned} \tan x \leftrightarrow \tan^{- 1} x \equiv \arctan x \end{aligned}$	$\begin{aligned} \tan x \leftrightarrow \cot^{- 1} x \equiv arccot x \end{aligned}$

The notation that uses “arc” as a prefix is an alternative way of indicating the inverse function.
::使用“弧”作为前缀的标记是表示反函数的另一种方式。

Now here is an important point to remember: since they all are periodic functions, none of trigonometric functions passes the horizontal line test. That is, they are not one-to-one functions. (Recall from Chapter 1, a function is one-to-one if and only if every element of its range corresponds to exactly one element of its domain.) But if we restrict the domain of each of the six trigonometric functions so that each function becomes one-to-one, we can define an inverse function for all six. And that is what is done.
::现在,这里需要记住一个重要点:由于它们都是定期函数,任何三角函数都不能通过水平线测试。也就是说,它们不是一对一的函数。 (从第一章中回顾,一个函数是一对一,如果其范围的每一元素都与其领域的一个元素完全对应的话。 ) 但如果我们限制六个三角函数的每一个域,以使每个函数成为一对一,我们就可以为所有六个函数确定一个反函数。这就是我们要做的。

The table below provides a brief summary of characteristics of the six inverse trigonometric functions.
::下表简要概述了六个逆三角函数的特征。

Inverse Function	Domain	Range	Basic Properties
$\begin{aligned} \sin^{- 1} x \end{aligned}$	$\begin{aligned} - 1 \leq x \leq 1 \end{aligned}$	$\begin{aligned} \frac{- π}{2} \leq y \leq \frac{π}{2} \end{aligned}$	$\begin{aligned} \sin^{- 1} (\sin x) = \sin (\sin^{- 1} x) = x \end{aligned}$
$\begin{aligned} \cos^{- 1} x \end{aligned}$	$\begin{aligned} - 1 \leq x \leq 1 \end{aligned}$	$\begin{aligned} 0 \leq y \leq π \end{aligned}$	$\begin{aligned} \cos^{- 1} (\cos x) = \cos (\cos^{- 1} x) = x \end{aligned}$
$\begin{aligned} \tan^{- 1} x \end{aligned}$	all $\begin{aligned} R \end{aligned}$	$\begin{aligned} (\frac{- π}{2}, \frac{π}{2}) \end{aligned}$	$\begin{aligned} \tan^{- 1} (\tan x) = \tan (\tan^{- 1} x) = x \end{aligned}$
$\begin{aligned} \csc^{- 1} x \end{aligned}$	$\begin{aligned} (- \infty, - 1] \cup [1, + \infty) \end{aligned}$ $\begin{aligned} \| x \| \geq 1 \end{aligned}$ ::1	$\begin{aligned} \frac{- π}{2} \leq y \leq \frac{π}{2} \end{aligned}$ ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ $\begin{aligned} y \neq 0 \end{aligned}$ ::y0	$\begin{aligned} \csc^{- 1} (\csc x) = \csc (\csc^{- 1} x) = x \end{aligned}$
$\begin{aligned} \sec^{- 1} x \end{aligned}$	$\begin{aligned} (- \infty, - 1] \cup [1 + \infty) \end{aligned}$ $\begin{aligned} \| x \| \geq 1 \end{aligned}$ ::1	$\begin{aligned} [0, \frac{π}{2}) \cup (\frac{π}{2}, π] \end{aligned}$	$\begin{aligned} \sec^{- 1} (\sec x) = \sec (\sec^{- 1} x) = x \end{aligned}$
$\begin{aligned} \cot^{- 1} x \end{aligned}$	all $\begin{aligned} R \end{aligned}$	$\begin{aligned} 0 < y < π \end{aligned}$	$\begin{aligned} \cot^{- 1} (\cot x) = \cot (\cot^{- 1} x) = x \end{aligned}$

The range is based on limiting the domain of the original function so that it is a one-to-one function.
::范围以限制原始函数域为基础,因此它是一个一对一的函数。

The graphs of the six inverse trigonometric functions are shown below.
::6个逆三角函数的图表如下所示。

Here is an example of how to use the :
::以下是如何使用:

What is the exact value of $\begin{aligned} \sin^{- 1} = (\frac{\sqrt{3}}{2}) \end{aligned}$ ?
::罪1=(32)的确切价值是多少?

This is equivalent to $\begin{aligned} \sin x = \frac{\sqrt{3}}{2} \end{aligned}$ .
::这相当于sinx=32。

Thus $\begin{aligned} \sin^{- 1} (\frac{\sqrt{3}}{2}) = \frac{π}{3} radians \end{aligned}$ .
::因此,Sin -1 (32) 3 弧度。

You can easily confirm this result by using the $\begin{aligned} 1 - \sqrt{3} - 2 \end{aligned}$ relationship for the sides of a 30-60-90 triangle and the definition of the sine function; or using your scientific calculator.
::您可以使用 30-60-90 三角形两侧的 1- 3-2 关系和正弦函数的定义, 或使用您的科学计算器, 轻松确认此结果。

The following identities are useful in relating inverse trigonometric functions:
::下列特征有助于将反三角函数联系起来:

\begin{aligned} \cos^{- 1} x & = \frac{π}{2} - \sin^{- 1} x \\ \cot^{- 1} x & = \frac{π}{2} - \tan^{- 1} x \\ \csc^{- 1} x & = \frac{π}{2} - \sec^{- 1} x \end{aligned}

Many calculators only have inverse sine, cosine, and tangent functions, so that calculating

\begin{aligned} \sec^{- 1} x \end{aligned}

\begin{aligned} \csc^{- 1} x \end{aligned}

can be cumbersome. But, practical ways to compute inverse secant, cosecant, and cotangent functions are:

\begin{aligned} \csc^{- 1} x & = \sin^{- 1} \frac{1}{x} \\ \sec^{- 1} x & = \cos^{- 1} (\frac{1}{x}) \\ \cot^{- 1} x & = \frac{π}{2} - \tan^{- 1} x \end{aligned}

::csc-1x=sin-11xsec-11xxx=cos-1}(1x)cot-11x_2-tan-1xxx

The relationship for $\begin{aligned} \sec^{- 1} x \end{aligned}$ is derived using the procedure:
::秒-1x 的关系使用以下程序产生:

If $\begin{aligned} \sec θ = \frac{1}{\cos θ} = x \end{aligned}$ , then $\begin{aligned} \cos θ = \frac{1}{x} \end{aligned}$ .
::如果 sec* 1cosx, 那么cos* 1x.

This means that $\begin{aligned} \cos^{- 1} (\cos θ) = \cos^{- 1} (\frac{1}{x}) = θ \end{aligned}$ .
::这意味着cos-1(cos)=cos-1(1x)。

Therefore the trick is: $\begin{aligned} \sec^{- 1} (\sec θ) = \sec^{- 1} x = \cos^{- 1} (\frac{1}{x}) \end{aligned}$
::因此,技巧是: 秒-1( sec) =sec- 1_ x=cos- 1( 1x)

The relationship for inverse cosecant can be derived in a similar fashion.
::反向的共生后代关系也可以以类似的方式产生。

Examples
::实例

Example 1
::例1

Find $\begin{aligned} \sec^{- 1} (3.24) \end{aligned}$ only using your calculator’s inverse sine, cosine, or tangent functions.
::仅使用您的计算器的反正弦、余弦或正切函数查找 second - 1\\\\\\\\ ( 3. 24) 。

Use the relationship: $\begin{aligned} \sec^{- 1} x = \cos^{- 1} (\frac{1}{x}) \end{aligned}$ .
::使用关系: 秒-1x=cos-11(1x) 。

Since
::自

\begin{aligned} \frac{1}{x} = \frac{1}{3.24} & = 0.3086, \\ \sec^{- 1} 3.24 & = \cos^{- 1} 0.3086 = 72^{\circ} \equiv \frac{2 π}{5} radians . \end{aligned}

::1x=13.24=0.3086,sec-13.24=cos-10.3086=7225弧度。

Example 2
::例2

Find the exact value of the composition $\begin{aligned} \sin (\arctan \frac{5}{12}) \end{aligned}$ .
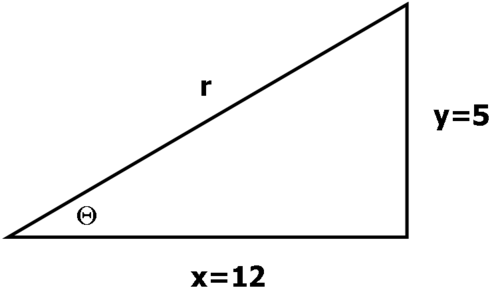
::查找组成成分的准确值 sin( arctan512) 。

The problem requires finding $\begin{aligned} \sin θ \end{aligned}$ , where $\begin{aligned} θ = \arctan \frac{5}{12} \end{aligned}$ .
::问题在于要找到sin, 在那里,arctan512。

The figure below can be used as reference.
::下图可作为参考。

If $\begin{aligned} θ = \arctan \frac{5}{12} \end{aligned}$ , then $\begin{aligned} \tan θ = \tan (\arctan \frac{5}{12}) = \frac{5}{12} = \frac{y}{x} \end{aligned}$ .
::若是 arctan512, 那么tann( 512) = 512=yx.

This means that $\begin{aligned} \sin θ = \frac{y}{r} = \frac{5}{\sqrt{12^{2} + 5^{2}}} = \frac{5}{\sqrt{169}} = \frac{5}{13} \end{aligned}$ .
::这意味着sinyr=5122+52=5169=513。

Therefore, $\begin{aligned} \sin (\arctan \frac{5}{12}) = \frac{5}{13} \end{aligned}$ .
::因此,sin(arctan512)=513。

Example 3
::例3

Find the exact value of the composition $\begin{aligned} \cot (\csc^{- 1} - \frac{13}{12}) \end{aligned}$ .
::查找构成的准确值 cot(csc-1-1312) 。

The problem requires finding $\begin{aligned} \cot θ \end{aligned}$ , where $\begin{aligned} θ = \csc^{- 1} - \frac{13}{12} \end{aligned}$ .
::这个问题需要找到Cot,那里是csc-1-1-11312。

From the identity $\begin{aligned} \csc^{- 1} x = \sin^{- 1} \frac{1}{x} \end{aligned}$ , we have $\begin{aligned} \csc^{- 1} - \frac{13}{12} = \sin^{- 1} - \frac{12}{13} = θ \end{aligned}$ , or $\begin{aligned} \sin θ = - \frac{12}{13} \end{aligned}$ . Since $\begin{aligned} \sin θ < 0 \end{aligned}$ , and the domain of $\begin{aligned} \sin θ \end{aligned}$ is $\begin{aligned} - \frac{π}{2} \leq θ \leq \frac{π}{2} \end{aligned}$ , we know $\begin{aligned} - \frac{π}{2} < θ < 0 \end{aligned}$ . This means that $\begin{aligned} \cos θ > 0 (\cos x = \cos (- x)) \end{aligned}$ , so $\begin{aligned} \cot θ < 0 \end{aligned}$ .
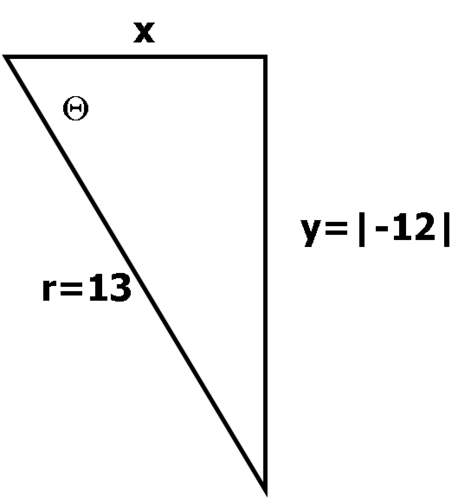
::从身份 csc - 1x=sin - 11x, 我们有csc - 1- 1312=sin - 1 - 1213, 或sin _ 1 - 1213, 或sin 1213}, 1223. 因为罪 0, 罪的范畴是 22, 我们知道 20。这意味着cos *0 (cosx=cos(-x)), so cot0。

We can use the figure below to determine $\begin{aligned} \cot θ \end{aligned}$ .
::我们可以用下图来决定Cot。

$\begin{aligned} \cot θ = \frac{1}{\tan θ} = - \frac{1}{\frac{12}{x}} = - \frac{1}{\frac{12}{\sqrt{13^{2} - 12^{2}}}} = - \frac{5}{12} \end{aligned}$
::一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一二一一二一一二一二一一二一一二一一一一二一一一一二一一一一一二一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一二一一一一一一一一一一一一一一一一一一一一一一一一一一二一一一一一一一一一一一一一一一二一一一二一一一二一一一一二一一一一二一一一一一一一一一二一一一一一一一一一一一一一一一一一一一一二一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一二一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一

Therefore, $\begin{aligned} \cot (\csc^{- 1} - \frac{13}{12}) = - \frac{5}{12} \end{aligned}$ .
::因此,Cot(csc-1-1312)512。

Review
::回顾

Find the exact value of each expression without using a calculator:
::在不使用计算器的情况下查找每个表达式的确切值 :

$\begin{aligned} \sin^{- 1} 0 \end{aligned}$
::和(第1)-(第1)-(第0)-(第1)-(第1)-(第1)-(第1)-(第0)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)-(第0)-(第1)-(第1)-(第1)-(第1)-(第1)-(第1)

$\begin{aligned} \arccos (- 1) \end{aligned}$
::arccos( - 1)

$\begin{aligned} \tan^{- 1} (- 1) \end{aligned}$
::tan- 1 (- 1)

$\begin{aligned} \cot^{- 1} (- \sqrt{3}) \end{aligned}$
:- 3) (- 3)

$\begin{aligned} arccsc (- 2) \end{aligned}$
::arccsc(-2)

$\begin{aligned} \sec^{- 1} \frac{2 \sqrt{3}}{3} \end{aligned}$
::空间 - 1233

$\begin{aligned} \arcsin (- \frac{\sqrt{2}}{2}) \end{aligned}$
::arcsin(- 22)

$\begin{aligned} \sin (\arccos \frac{1}{4}) \end{aligned}$
:arccos14) (arccos14)

$\begin{aligned} \tan (\arccos \frac{3}{4}) \end{aligned}$
::~ (arccos34) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$\begin{aligned} \sin (\tan^{- 1} \frac{3}{2}) \end{aligned}$
:tan -132) (tan -132)

$\begin{aligned} \sec (\csc^{- 1} - \frac{15}{8}) \end{aligned}$
:csc-1-158) (csc-1-158)

$\begin{aligned} \cos (\sin^{- 1} \frac{2}{3}) \end{aligned}$
::COs(sins-123)

$\begin{aligned} \sin (\tan^{- 1} \frac{3}{2}) \end{aligned}$
:tan -132) (tan -132)

$\begin{aligned} \sec (\cot^{- 1} - \frac{15}{8}) \end{aligned}$
:cot-1-158) (cot-1-158)

$\begin{aligned} \tan (\cos^{- 1} - \frac{5}{13}) \end{aligned}$
:cos-1-513) (cos-1-513)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Inverse Trigonometric Functions ::反逆三角函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)