Section: 其他特别极地方和图 | 10.12 其他特别极地方和图

Section outline

Max is in charge of the sound system for his big sister’s wedding reception. He can’t get into the hall until the morning of the wedding, so he’s going to have to set up his microphones and speakers in record time. He does, however, have a floor plan of the hall. How can he make sure that the pick-up areas of the microphones and the broadcast area of the speakers don’t overlap and cause feedback? He’ll have time for some minimal trial and error, but he needs to have a general idea where all the microphones and speakers will be during the reception. Can he use to help him place his equipment?
::麦克斯负责他大姐的婚礼招待会的音响系统。他不能进入大厅直到婚礼的上午,所以他不得不在创纪录的时间内安装麦克风和扬声器。然而,他有一个大厅的地板图。他如何确保麦克风的接收区和发言者的广播区不会重叠和产生反馈?他有时间做一些微小的试验和错误,但他需要有一个一般的想法,在招待会期间所有的麦克风和扬声器都在哪里。他能用来帮助他安装设备吗?

More Polar Equations and Graphs
::更多极地方和图

Why do people continue to use polar coordinates when modern computers are powerful and fast enough to solve extremely complicated problems in rectangular form ? One reason is that many polar graphs are beautiful and intriguing. Polar graphs can help people see patterns that they might otherwise overlook. Artists have even used polar graphs as the basis of their designs.
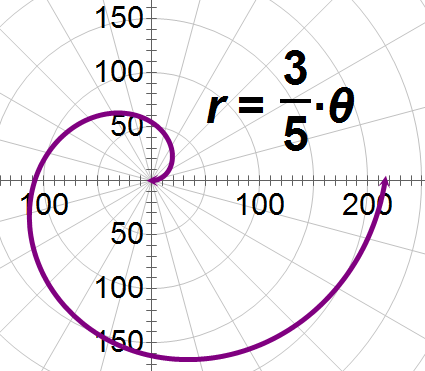
::当现代计算机强大而快速,足以解决极端复杂的矩形问题时,人们为什么继续使用极地坐标? 原因之一是许多极地图是美丽而有趣的。极地图可以帮助人们看到他们可能忽略的模式。艺术家甚至用极地图作为设计的基础。

One of the simplest equations that forms a special polar curve is $\begin{aligned} r = a θ \end{aligned}$ , where $\begin{aligned} a \end{aligned}$ is any real number and $\begin{aligned} θ \end{aligned}$ ranges from zero to infinity. Equations of this form create a shape known as an Archimedean spiral . As $\begin{aligned} θ \end{aligned}$ increases, the graph continues to spiral out like a perfect snail’s shell. The following graphs demonstrate how changing the value of $\begin{aligned} a \end{aligned}$ alters the spiral. Note that each curve will continue to spiral forever.
::形成特殊极曲线的最简单的方程式之一是 r=a, 其中一个是一个实际数字, 和从零到无穷不等。这种形态的方程式的方程式创造了一个被称为Archimedean 螺旋的形状。随着的增加, 图形继续像一只完美的蜗牛的外壳一样螺旋。下图显示一个螺旋的值是如何改变的。注意每个曲线将永远螺旋。

Another important polar curve is the cardioid . People who work with acoustics know that the cardioid is an accurate model for both the pick-up range of certain types of microphones and the broadcast range for certain kinds of speakers. Cardioids get their name from their heart-like shapes. Equations of the form $\begin{aligned} r = 1 + a \cos θ \end{aligned}$ produce cardioid curves. You can change the orientation of a cardioid, or of any other polar equation with cosine in its standard form, by replacing cosine with sine, negative cosine, or negative sine.
::另一个重要的极地曲线是心类。从事声学工作的人知道,心类是一个精确的模型,既可以接收某些类型的麦克风,也可以传播某些类型的发言者。心类是从心型形状中取名的。表R=1+acos的方程式的方程式产生心类曲线。你可以改变心类板或任何其他极性方程式的方向,用标准形式的焦线,用正弦、负正弦或负正弦取代正弦。

Rose curves are another interesting set of polar curves. For these equations of the form $\begin{aligned} r = a \cos n θ \end{aligned}$ , where $\begin{aligned} n \end{aligned}$ is a natural number, the plots resemble flowers. When $\begin{aligned} n \end{aligned}$ is odd, the flowers have $\begin{aligned} n \end{aligned}$ petals, and when $\begin{aligned} n \end{aligned}$ is even, the flowers have $\begin{aligned} 2 n \end{aligned}$ petals.
::玫瑰曲线是另一组有趣的极地曲线。对于表单 r=acosn( n) 是自然数字的这些方程式, 地块与花朵相似。奇特时, 花朵有正花瓣, 偶数时, 花朵有2n 花瓣。

You can use your graphing calculator or other technology to help you graph all of these polar curves.
::您可以使用您的图形计算器或其他技术来帮助您绘制所有这些极曲线的图表。

With this knew information, w hat is the shape of the graph of the polar equation $\begin{aligned} 6 r = 5 + 5 \sin θ \end{aligned}$ ?
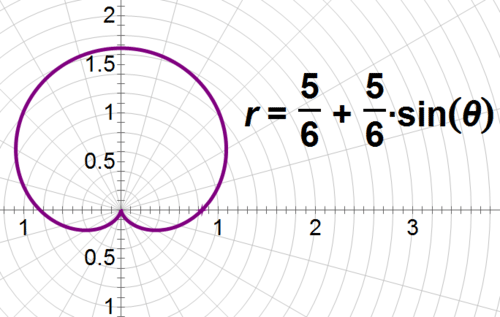
::以这些已知的信息, 极方平方程式 6r=5+5sin 的图形的形状是什么?

First, isolate $\begin{aligned} r \end{aligned}$ to get $\begin{aligned} r = \frac{5}{6} + \frac{5}{6} \sin θ \end{aligned}$ . This graph appears most similar to the cardioid curve, which is $\begin{aligned} r = 1 + a \cos θ \end{aligned}$ . However, the changes to the form mean that the graph will be rotated by $\begin{aligned} \frac{π}{2} \end{aligned}$ and slightly smaller than the standard cardioid. Now, graph the equation to test the predictions.
::首先,从 r 中分离 r 以获得 r= 56+56sin 。此图似乎与 carioble 曲线( r= 1+acos ) 最相似。然而, 窗体的修改意味着 rg 将被 2 旋转, 且略小于标准 r 类。现在, 请绘制方程式来测试预测。

Now, let's describe the graph of $\begin{aligned} r = - 8 \sin (32 θ) \end{aligned}$ , then graph it.
::现在,让我们描述一下 r8sin( 32) 的图表, 然后绘制图。

This graph matches the format for a rose curve: $\begin{aligned} r = a \cos n θ \end{aligned}$ . Since $\begin{aligned} n \end{aligned}$ is even the final graph should have 64 petals. The – sine means that the graph will be rotated $\begin{aligned} - \frac{π}{2} \end{aligned}$ radians from its starting position.
::此图表符合玫瑰曲线的格式 : r=acosn。由于 n 甚至是最后的图形, 应该有 64 个花瓣。字符串意味着图形将从起始位置旋转 2 弧度。

Examples
::实例

Example 1
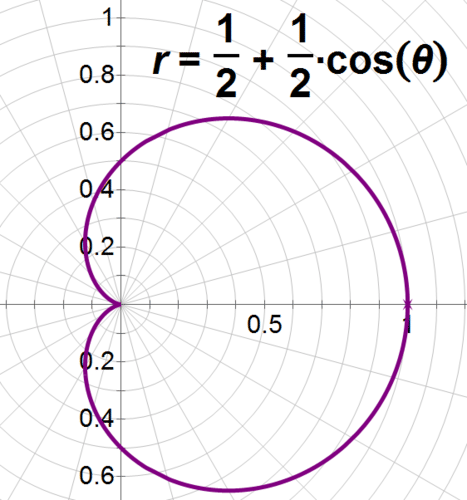
::例1

Earlier, you were asked how Max can set up the sound system for his sister's wedding so that the speakers don't overlap. Max can use cardioids to help him set up the sound system without causing feedback. He researches his microphones and speakers online and finds out that the pick-up pattern of his microphones can be graphed using the equation $\begin{aligned} r = \frac{1}{2} + \frac{1}{2} \cos θ \end{aligned}$ . Since he has multiple microphones to place, he can graph the curve and use it with his floor plan to ensure that the mikes don’t overlap and that he places the speakers in the dead zones behind the microphones, where they won’t pick up any sound.
::早些时候,有人问您Max如何为他姐姐的婚礼设置音响系统,以使发言者不发生重叠。 Max可以使用类固醇帮助他建立音响系统,而不会引起反馈。他在线研究他的麦克风和扬声器,发现他的麦克风的接听模式可以用方程式 r=12+12cos来绘制。由于他有多个麦克风,他可以绘制曲线图,用他的平面图确保麦克风不发生重叠,并将喇叭放在麦克风后面的死区,他们在那里不会听到任何声音。

Since the microphones pick up along the polar axis between 0 and 1, he’ll want to position speakers in the dead zone, where $\begin{aligned} r < 0 \end{aligned}$ , and $\begin{aligned} θ = 0 \end{aligned}$ . He can also position speakers at other places in the dead zone, but cardioid microphones are least likely to pick up sound when it’s $\begin{aligned} π \end{aligned}$ radians from their optimal pick-up areas.
::由于麦克风在0:1到1之间沿着极轴移动,他想将发言者安置在死区,那里有r < 0 和 0。他也可以将发言者安置在死区的其他地点,但是,当心形麦克风从其最佳取款区升起时,心型麦克风最不可能听到声音。

Example 2
::例2

Describe what the graph $\begin{aligned} r = - 3 θ \end{aligned}$ will look like. Then, change the equation to rotate it by $\begin{aligned} π \end{aligned}$ radians. Graph the original and rotated graphs.
::描述图形 r 3 的外观。然后, 将方程式修改为弧度旋转。绘制原始和旋转的图形。

The graph will make an Archimedean spiral three times larger than the normal one. To rotate the graph, change the -3 to 3.
::图形将使 Archimedean 螺旋轴比正常螺旋轴大三倍。要旋转图形, 请将 - 3 改为 3 。

For each of the following examples , identify the polar curve given by the equation and then graph it.
::对于以下每个示例,请标明方程式给出的极曲线,然后绘制图表。

Example 3
::例3

$\begin{aligned} 6 \cos 4 θ - 3 r = 0 \end{aligned}$
::6cos43r=0

First, solve for $\begin{aligned} r \end{aligned}$ . Then, identify the equation.
::首先,解决r。然后,确定方程。

$\begin{aligned} 6 \cos 4 θ - 3 r & = 0 \\ 3 r & = 6 \cos 4 θ \\ r & = 2 \cos 4 θ \end{aligned}$

::6cos43r=03r=6cos}4r=2cos443r=03r=6cos}

The graph will be of a rose curve with 8 petals.
::图表将显示玫瑰曲线8个花瓣。

Example 3
::例3

$\begin{aligned} 5 r = 3 θ \end{aligned}$
::5r=3

First, solve for $\begin{aligned} r \end{aligned}$ . Then, identify the equation.
::首先,解决r。然后,确定方程。

$\begin{aligned} 5 r & = 3 θ \\ r & = \frac{3}{5} θ \end{aligned}$

::5r=3r=35

The graph will be Archimedean spiral.
::图表将是Archimedean螺旋。

Example 5
::例5

$\begin{aligned} 5 r - 25 + 45 \cos 3 θ = 0 \end{aligned}$
::5r-25+45cos 30

First, solve for $\begin{aligned} r \end{aligned}$ . Then, identify the equation.
::首先,解决r。然后,确定方程。

$\begin{aligned} 5 r - 25 + 45 \cos 3 θ = 0 \\ 5 r = 25 - 45 \cos 3 θ \\ r = 5 - 9 \cos 3 θ \end{aligned}$

::5-25+45cos 305r=25-45cos 33r=5-9cos

At first glance, this equation looks similar to a cardioid. However, it also has $\begin{aligned} n θ \end{aligned}$ like a rose curve. You’ll have to graph it to get a good sense for what the combination does - it’s a rose curve within a rose curve!
::乍一看,这个方程式看起来像一个心形。但是,它也像玫瑰曲线一样。您必须用图表来了解组合的作用 — — 玫瑰曲线中的玫瑰曲线!

However, take out the three, graph $\begin{aligned} r = 5 - 9 \cos θ \end{aligned}$ , and you’ll get a curve similar to a cardioid curve. This equation illustrates how small changes can produce complicated, beautiful, polar graphs.
::然而,取出三个图,图 r=5-9cos,你会得到一个类似于类心形曲线的曲线。这个方程式可以说明小变化如何产生复杂、美丽、极极图。

Review
::回顾

For #1-3, describe the family of equations that produces that curve.
::#1-3,描述产生曲线的方程式的组合。

Rose curve
::玫瑰曲线

Archimedean spiral
::拱形螺旋螺旋

Cardioid curve
::心心形曲线

For #4-15, identify the polar curve and then graph it.
::4 -15 标明极曲线,然后绘制图表。

$\begin{aligned} \frac{r}{2} = θ \end{aligned}$
::r2

$\begin{aligned} r = 1 - 4 \cos θ \end{aligned}$
::r=1 - 4cos

$\begin{aligned} 3 r = 4 \cos (8 θ) \end{aligned}$
::3r=4cos( 8)

$\begin{aligned} r = \frac{1}{2} + \frac{1}{2} \cos (θ) \end{aligned}$
::r=12+12cos

$\begin{aligned} r = - θ \end{aligned}$
::瑞里里里里里

$\begin{aligned} \frac{r}{4} = 4 \cos (4 θ) \end{aligned}$
::r4=4cos(4)

$\begin{aligned} r = - 4 θ \end{aligned}$
::r 4

$\begin{aligned} r = - 2 \sin (8 θ) \end{aligned}$
::r2sin(8)

$\begin{aligned} r = 1 - \sin θ \end{aligned}$
::r=1-sin

$\begin{aligned} 1 = \cos θ + r \end{aligned}$
::1=cosr

$\begin{aligned} r = 5 \end{aligned}$
::rm=5

$\begin{aligned} r = 5 θ \end{aligned}$
::r=5

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

More Polar Equations and Graphs ::更多极地方和图

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 3 ::例3

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

More Polar Equations and Graphs
::更多极地方和图

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 3
::例3

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)