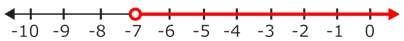Course: 7.14 双重不平等 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 双重不平等

Collapse Expand
双重不平等
Marcia and Joe need to collect dragonflies and gather data about them for biology class. They need to capture at least 32 dragonflies for their project. They have already collected 3 dragonflies, and they can gather 2 dragonflies on average each hour. What is the minimum number of hours that Marcia and Joe need to search to get at least 32 dragonflies? Can you write an expression that models this information?
::玛西娅和乔需要收集龙蝇, 并收集生物类的数据。他们需要至少捕捉32只龙蝇。他们已经收集了3只龙蝇, 每小时平均可以收集2只龙蝇。玛西娅和乔需要搜索的最小时数是多少才能找到至少32只龙蝇? 您能写一个模型来模拟这些信息的表达方式吗 ?

In this concept, you will learn to solve inequalities and graph solutions.
::在这个概念中,你将学会解决不平等和图表解决方案。

Solving Two-Step Inequalities
::解决双步不平等

Inequalities are solved in almost the same way as regular equations. There are two small differences.
::不平等的解决方式几乎与正常方程式相同。有两个小的差别。

When solving for the variable in an inequality , if you multiply or divide each side of the equation by a negative number the direction of the inequality changes.
::在解决不平等变量时,如果将方程的方程每一侧乘以负数或除以负数,不平等的方向就会发生变化。

Unlike a regular equation, it is common to graph the solution set for an inequality on a number line.
::与常规等式不同,通常用数字线来说明为不平等设定的解决办法。

Let’s look at an example.
::让我们举个例子。

Solve this inequality and graph its solution on a number line $\begin{aligned} n - 4 \leq 3 \end{aligned}$ .
::解决这种不平等,用数字线n-43来说明其解决办法。

Solve the inequality as you would solve an equation, by using inverse operations and applying the properties of equality (e.g. the addition property of equality). Since the 4 is subtracted from $\begin{aligned} n \end{aligned}$ , add 4 to both sides of the inequality to solve it.
::通过使用反向操作和运用平等特性(例如,增加平等财产)来解决不平等问题,因为从n减去了4项,在不平等的两侧增加4项以解决不平等问题。

$\begin{aligned} \begin{array}{rcl} n - 4 & \leq & 3 \\ n - 4 + 4 & \leq & 3 + 4 \\ n + 0 & \leq & 7 \\ n & \leq & 7 \end{array} \end{aligned}$

::n43n-4+43+4n+07n+7

The answer is $\begin{aligned} n \leq 7 \end{aligned}$ .
::答案是n7。

Next, graph the solution. The inequality $\begin{aligned} n \leq 7 \end{aligned}$ is read as “ $\begin{aligned} n \end{aligned}$ is less than or equal to 7.” So, the solution of this inequality includes 7 and all numbers that are less than 7.
::下图请说明解决方案。n7的不平等被解读为“不小于或等于7.7。” 因此,解决这一不平等的办法包括7个,所有数字小于7个。

Draw a number line from 0 to 10. Add a closed circle at 7 to show that 7 is a solution for this inequality. Then draw an arrow pointing to the left showing all numbers less than 7.
::从 0 到 10. 添加一个 7 的封闭圆以显示 7 是此不平等的解决方案。然后向左绘制箭头, 显示所有小于 7 的数字。

The solution set is graphed above.
::解决方案集的图解如上。

Let’s look at another example.
::让我们再看看另一个例子。

Solve this inequality and graph its solution on a number line $\begin{aligned} - 2 n < 14 \end{aligned}$ .
::解决这种不平等,用数字线2n < 14来说明其解决办法。

Since $\begin{aligned} n \end{aligned}$ is multiplied by -2, divide both sides of the inequality by -2 to isolate the variable .
::由于 n 乘以-2, 将不平等的两边除以-2, 以孤立变量。

When working with inequalities if you divide or multiply both sides of the equation by a negative number the inequality must change directions. This means changing the inequality symbol from a “less than” symbol (<) to a “greater than” symbol (>).
::在处理不平等时,如果您将等式的两边除以负数或乘以负数,不平等必须改变方向。这意味着不平等符号从“小于”符号(<)改为“大于”符号(>)。

$\begin{aligned} \begin{array}{rcl} - 2 n & < & 14 \\ \frac{- 2 n}{- 2} & > & \frac{14}{- 2} \\ 1 n & > & - 7 \\ n & > & - 7 \end{array} \end{aligned}$

::-2n <14-2n-2n-2>14-21-21n @ @7n @7_7_7_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2n_2_2n_2n_2n_2_2n_2n_2n_2n_2_2n_2_2_2n_2n_2n_2_2n_2n_2n_2n_2_2n_2n_2n_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_

The answer is $\begin{aligned} n > - 7 \end{aligned}$ .
::答案是n7。

Next, graph the solution. The inequality $\begin{aligned} n > - 7 \end{aligned}$ is read as “ $\begin{aligned} n \end{aligned}$ is greater than -7.” So, the solution of this inequality includes all numbers that are greater than -7, but not -7.
::下一位请绘制解决方案图。不平等 n7 被解读为“n 大于-7 ” 。因此,这种不平等的解决方案包括所有大于 - 7, 但不大于 - 7 的数字。

Draw a number line from -10 to 0. Add an open circle at -7 to show that -7 is not a solution for this inequality. Then draw an arrow pointing to the right which shows all numbers greater than -7 are included in the solution.
::绘制 - 10 到 0 之间的数字行。在 - 7 处添加一个开放圆以显示 - 7 不是解决这个不平等的办法。然后绘制指向右边的箭头, 该箭头显示的数值大于 - 7 的所有数字都包含在解决方案中。

The answer is $\begin{aligned} n > - 7 \end{aligned}$ , and the graph of its solution is shown above.
::答案是n7,其解决方案图见上文。

Sometimes, it will take more than one step to solve an inequality. Solve these problems as if there were an equals sign, but remember that if you multiply or divide by a negative number the inequality will change direction.
::有时,解决不平等问题需要不止一步的时间。解决这些问题要像一个同等的标志一样,但要记住,如果你把不平等问题乘以负数或除以负数,不平等问题就会改变方向。

Here is an example of a two-step inequality.
::这是两步不平等的一个例子。

Solve the inequality $\begin{aligned} \frac{n}{3} + 9 \geq - 9 \end{aligned}$ .
::解决不平等n3+99。

This problem is done just like a two-step equality.
::这个问题就像两步平等一样。

First, isolate the $\begin{aligned} \frac{n}{3} \end{aligned}$ term . Subtract 9 from both sides of the inequality.
::首先,将n3词分开,从不平等的两侧减去9。

$\begin{aligned} \begin{array}{rcl} \frac{n}{3} + 9 & \geq & - 9 \\ \frac{n}{3} + 9 - 9 & \geq & - 9 - 9 \\ \frac{n}{3} & \geq & - 18 \end{array} \end{aligned}$

::n3+9_9_9_9_9_9_9_9_9_9_9_3_18_

Now, you have a one-step inequality, which is easier to solve. Since you will not be multiplying or dividing by a negative number the inequality will not change direction. Multiply both sides of the inequality by 3, to isolate the variable $\begin{aligned} n \end{aligned}$ .
::现在,你有一个单步不平等,这更容易解决。既然你不会以负数乘以或除以负数,那么不平等不会改变方向。将不平等的两边乘以3,以孤立变量n。

$\begin{aligned} \begin{array}{rcl} \frac{n}{3} \times 3 & \geq & - 18 \times 3 \\ \frac{3}{3} \times n & \geq & - 54 \\ 1 n & \geq & - 54 \\ n & \geq & - 54 \end{array} \end{aligned}$

::n3x3\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\...\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

The answer is $\begin{aligned} n \geq - 54 \end{aligned}$ .
::答案是n54。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the dragonfly project.
::早些时候,你得到一个问题关于项目。

Marcia and Joe need to gather at least 32 dragonflies for their project. They have 3 already and can collect 2 each hour. Can you write an inequality that describes this situation?
::玛西亚和乔需要收集至少32只龙的作品。他们已经有3只了, 每小时可以收集2只。您能写一个描述这种情况的不平等吗 ?

First, let $\begin{aligned} h \end{aligned}$ be the number of hours spent collecting. They collect two per hour, or $\begin{aligned} 2 h \end{aligned}$ dragonflies. They start with 3. So, if the students work $\begin{aligned} h \end{aligned}$ hours they will have $\begin{aligned} 3 + 2 h \end{aligned}$ dragonflies. They need at least 32 dragonflies, so $\begin{aligned} 3 + 2 h \end{aligned}$ needs be equal or greater than 32.
::首先,让我们来计算收集的小时数。它们每小时收集两个小时, 或2个小时。它们从3开始。所以, 如果学生工作时数为3小时, 他们就会有3+2小时的。他们至少需要32只龙, 所以3+2小时需要等于或大于32只。

The following inequality describes this situation.
::以下不平等情况说明了这种情况。

$\begin{aligned} 3 + 2 h \geq 32 \end{aligned}$

::3+2h32

Now, solve the inequality.
::现在,解决不平等问题。

First, isolate $\begin{aligned} 2 h \end{aligned}$ by subtracting 3 from both sides of the equation.
::首先,从方程的两侧减去3,将2h分离出来。

$\begin{aligned} \begin{array}{rcl} 3 - 3 + 2 h & \geq & 32 - 3 \\ 0 + 2 h & \geq & 29 \\ 2 h & \geq & 29 \end{array} \end{aligned}$

::3-3+2h-32-330+2h-2992-29

Next, isolate the variable $\begin{aligned} h \end{aligned}$ , and divide both sides by 2.
::其次,将变量h分离出来,将两边除以2。

$\begin{aligned} \begin{array}{rcl} \frac{2 h}{2} & \geq & \frac{29}{2} \\ \frac{2}{2} h & \geq & 14.5 \\ 1 h & \geq & 14.5 \\ h & \geq & 14.5 \end{array} \end{aligned}$

::2h229222h14.51h145.5h14.5。

Finally, interpret the results. The students have to work at least 14.5 hours to collect 32 dragonflies. If you assume they need the full hour to collect the two dragonflies for that last hour, they should work 15 hours.
::最后,请解释结果。学生们必须至少工作14.5小时才能收集32只。如果你认为他们需要一小时的时间来收集这两只,那么他们应该工作15小时。

The answer is the students need to collect dragonflies for 15 hours.
::答案是学生们需要收集 15小时的蝗虫。

Example 2
::例2

Antonio is buying milk for a breakfast event. Each container of milk costs $3. At most, he can spend $12 on milk for the event.
::安东尼奥在为早餐活动买牛奶,每箱牛奶费用为3美元,最多12美元,他可以花在牛奶上。

Write an inequality to represent, $\begin{aligned} c \end{aligned}$ , the number of containers of milk he can buy.
::写一篇不平等的文章来代表, c,他可以买到多少箱牛奶。

Could Antonio buy 4 containers of milk for the event? Explain.
::安东尼奥可以买四箱牛奶吗?

Consider part a first.
::考虑第一部分。

Since each container of milk costs $3, you can find the total cost, in dollars, of the milk he buys by multiplying the number of containers by 3. The phrase “at most” indicates that you should use the $\begin{aligned} \leq \end{aligned}$ symbol.
::由于每箱牛奶费用为3美元,他购买牛奶的总成本以美元计算,将集装箱数乘以3。 “最多”一词表示您应该使用______符号。

The answer is $\begin{aligned} 3 c \leq 12 \end{aligned}$ .
::答案是3cQ12。

Note that the value of $\begin{aligned} c \end{aligned}$ must also be an integer greater than or equal to 0. Think about why that is for a moment.
::请注意 c 的值也必须是一个大于或等于 0 的整数。想想为什么这是暂时的。

The reason that the value of $\begin{aligned} c \end{aligned}$ must be an integer greater than or equal to zero is because Antonio cannot buy a negative number of containers nor can he buy a fraction of a container. Neither of those situations makes sense in real life. When using inequalities to represent real-life situations, you should always think about which values would make sense for the variable and which values would not make sense.
::因为安东尼奥不能购买负数集装箱,也不能购买部分集装箱,所以C的数值必须是大于或等于零的整数。这些情况在现实生活中都没有意义。当使用不平等来代表真实生活状况时,你应该总是想一想哪些值对变量有意义,哪些值对变量没有意义。

Next, consider part b.
::下一步,考虑B部分。

Solve $\begin{aligned} 3 c \leq 12 \end{aligned}$ to help you answer if he can buy 4 containers of milk.
::解决3c*12 帮助你回答如果他能买4箱牛奶的话

First, divide both sides of the equation by 3 to isolate the variable.
::首先,将方程两侧除以3,以孤立变量。

$\begin{aligned} \begin{array}{rcl} 3 c & \leq & 12 \\ \frac{3 c}{3} & \leq & \frac{12}{3} \\ \frac{3}{3} c & \leq & 4 \\ 1 c & \leq & 4 \\ c & \leq & 4 \end{array} \end{aligned}$

::3c123c3}12333c}41c}4c}4c}3c§23c3}123c3c}123cc}4c}4c§4}3c§123c}123c}123c}123cc}123cc}41c}4c}4c}4}

According to the inequality above, the number of containers, $\begin{aligned} c \end{aligned}$ , that he can buy must be less than or equal to 4.
::根据上述不平等情况,他可以购买的集装箱数量(c)必须小于或等于4个。

So, the answer is yes, Antonio can buy 4 containers of milk for the event.
::所以,答案是是是的,安东尼奥可以买4箱牛奶来参加这次活动。

Solve each inequality.
::解决每一种不平等。

Example 3
::例3

$\begin{aligned} x - 4 < 10 \end{aligned}$
::x-4 < 10

Add 4 to both sides of the equation to isolate the variable $\begin{aligned} x \end{aligned}$ .
::在方程的两侧添加 4 ,以孤立变量 x 。

$\begin{aligned} \begin{array}{rcl} x - 4 & < & 10 \\ x - 4 + 4 & < & 10 + 4 \\ x + 0 & < & 14 \\ x & < & 14 \end{array} \end{aligned}$

::x-4 < 10x-4+4 < 10+4x+0 < 14x < 14

The answer is $\begin{aligned} x < 14 \end{aligned}$ .
::答案是 x<14 。

Example 4
::例4

$\begin{aligned} 2 y + 4 \geq 12 \end{aligned}$
::2y+412

First, subtract both sides of the equation by -4 to isolate the term $\begin{aligned} 2 y \end{aligned}$ .
::首先,将方程的两边除以 - 4, 以孤立 2y 。

$\begin{aligned} \begin{array}{rcl} 2 y + 4 & \geq & 12 \\ 2 y + 4 - 4 & \geq & 12 - 4 \\ 2 y & \geq & 8 \end{array} \end{aligned}$

::2y+4122y+4-4-412-42y8

Now you have a single-step inequality, which is easier to solve. Divide both sides of the equation by 2 to isolate the variable $\begin{aligned} y \end{aligned}$ .
::现在,你有一个单步不平等,这更容易解决。将方程式的两边除以 2 以孤立变量 y 。

$\begin{aligned} \begin{array}{rcl} \frac{2 y}{2} & \geq & \frac{8}{2} \\ \frac{2}{2} y & \geq & 4 \\ 1 y & \geq & 4 \\ y & \geq & 4 \end{array} \end{aligned}$

::2y28222y41y4y4

The answer is $\begin{aligned} y \geq 4 \end{aligned}$ .
::答案是y4。

Example 5
::例5

$\begin{aligned} - 4 x \leq 16 \end{aligned}$
::- 4x16

First, divide both sides of the equation by -4. You will have to change the direction of the inequality when you do this because you are dividing by a negative number.
::首先,将等式两边除以 - 4。当您这样做时, 您必须改变不平等的方向, 因为您正在除以负数。

$\begin{aligned} \begin{array}{rcl} - 4 x & \leq & 16 \\ \frac{- 4 x}{- 4} & \geq & \frac{16}{- 4} \\ \frac{- 4}{- 4} x & \geq & - 4 \\ 1 x & \geq & - 4 \\ x & \geq & - 4 \end{array} \end{aligned}$

::- 4x16 - 4x416 - 4- 4- 4- 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_ 4x_

The answer is $\begin{aligned} x \geq - 4 \end{aligned}$ .
::答案是 x4。

Review
::回顾

Solve each inequality.
::解决每一种不平等。

$\begin{aligned} x + 4 < 10 \end{aligned}$
::x+4 < 10

$\begin{aligned} x - 3 \geq 7 \end{aligned}$
::x-37

$\begin{aligned} b + 5 \leq 15 \end{aligned}$
::b+5+15

$\begin{aligned} a - 7 \geq 14 \end{aligned}$
::a-714

$\begin{aligned} 4 y > 20 \end{aligned}$
::4y>20

$\begin{aligned} 6 x \leq 18 \end{aligned}$
::6x_18 6x_18

$\begin{aligned} - 4 y < - 12 \end{aligned}$
::-412

$\begin{aligned} - 5 x < - 20 \end{aligned}$
::- 5x% 20

$\begin{aligned} \frac{x}{2} \leq 10 \end{aligned}$
::x210

$\begin{aligned} \frac{x}{5} \leq 6 \end{aligned}$
::x56

$\begin{aligned} 2 x + 5 \geq 7 \end{aligned}$
::2x+5+7+7

$\begin{aligned} 3 y - 2 \leq 4 \end{aligned}$
::3y-24

$\begin{aligned} 3 a - 7 > 11 \end{aligned}$
::3a-7>11

$\begin{aligned} 2 b + 9 < 39 \end{aligned}$
::2b+9 < 39

$\begin{aligned} 2 x - 8 < 42 \end{aligned}$
::2x-8 < 42

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

双重不平等

Solving Two-Step Inequalities ::解决双步不平等

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Solving Two-Step Inequalities
::解决双步不平等

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)