7.17 线性方平方图

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节线性方形图

  折叠 展开

  线性方形图

  

  播放段落

  Dana is collecting information about caterpillars for science class. She’s comparing the lengths and widths of several caterpillars. Dana puts the data she has so far into a table. Dana is convinced there is a pattern . Can organize this information as a set of ordered pairs, graph it on a coordinate plane and write an equation that could model this?
  ::Dana正在收集科学类毛虫的信息。 她正在比较几只毛虫的长度和宽度。 Dana将她迄今掌握的数据放在一张表格中。 Dana相信有一个模式。 Dana可以将这些信息组织成一组定购配对,在坐标平面上绘制图表,并写出一个可以模拟这个模式的方程式?

  播放段落

  $$\begin{array}{r}\begin{array}{|cc|}\hline x\text{ (width in cm)}& y\text{ (length in cm)}\\ 2& 2\\ 3& 4\\ 4& 6\\ 5& 8\\ 6& 10\\ \hline\end{array}\end{array}$$

   
  In this concept, you will learn to graph on the coordinate plane.
  ::在此概念中,您将学会在坐标平面上绘制图表。

  播放段落

  Graphing Linear Functions
  ::直线函数

  播放段落

  A linear function is a specific type of function . You may notice that the word “line” is part of the word “linear”. That fact can help you remember that when a linear function is graphed on a coordinate plane, its graph will be a straight line.
  ::线性函数是一种特定类型的函数。您可能会注意到,“线性”一词是“线性”一词的一部分。这一事实可以帮助您记住,当线性函数在坐标平面上绘制图时,其图将是一个直线线。

  播放段落

  You can represent a function as a set of ordered pairs, through a table, and as an equation. You can also take the information in ordered pairs or in a table and represent a function as a graph.
  ::您可以通过表格和方程式代表一组有顺序的对子函数。您也可以以有顺序的对子或表格的形式接收信息,并代表一个图形函数。

  播放段落

  Let’s look at an example.
  ::让我们举个例子。

  播放段落

  The table of values below represents a function on a coordinate plane. On a coordinate plane, graph the linear function that is represented by the ordered pairs in the table below.
  ::下表所列数值表表示坐标平面上的函数。在坐标平面上,请绘制下表中定购对子所代表的线性函数图。

  播放段落

  $$\begin{array}{r}\begin{array}{|cc|}\hline x& y\\ \text{-}4& 5\\ \text{-}2& 3\\ 0& 1\\ 2& \text{-}1\\ 4& \text{-}3\\ \hline\end{array}\end{array}$$

  
  ::Xy-45-23012-14-3

  播放段落

  You can represent the information in this table as a set of ordered pairs  $\begin{array}{r}\{(-4,5),(-2,3),(0,1),(2,-1),(4,-3)\}\end{array}$ .
  ::您可以以一组有顺序的对{(- 4, 5, 5, (-2, 2, 3, 0, 1), (2, 1), (4, 3)} 来表示此表格中的信息 。

  播放段落

  Plot those five points on the coordinate plane. Then, connect them as shown below.
  ::在坐标平面上标出这五个点,然后将它们连接起来,如下文所示。

  

  播放段落

  Notice that the graph of this linear function is a straight line.
  ::注意此线性函数的图形为直线。

  播放段落

  You can also graph a linear function if you are given an equation for that function. This will involve a few more steps. When you have an equation, you can use the equation to create a table. Then, plot several of the ordered pairs in the table and connect them with a line.
  ::如果给您给出了该函数的方程式,您也可以绘制线性函数。这将涉及几个步骤。如果您有一个方程式,您可以使用方程式来创建表格。然后,绘制表格中几个有顺序的对,并将它们与直线连接。

  播放段落

  Here is another example.
  ::下面是另一个例子。

  播放段落

  The equation $\begin{array}{r}y=2x-1\end{array}$  is a linear function. Graph that function on a coordinate plane.
  ::y=2x- 1 等式是一个线性函数。 图形在坐标平面上起作用 。

  播放段落

  First, use the equation to create a table and find several ordered pairs for the function. It is a good idea to use some negative $\begin{array}{r}x\end{array}$ -values, some positive $\begin{array}{r}x\end{array}$ -values and 0. For example, you can create a table to find the values of $\begin{array}{r}y\end{array}$  when $\begin{array}{r}x\end{array}$  is equal to -2, -1, 0, 1, and 2.
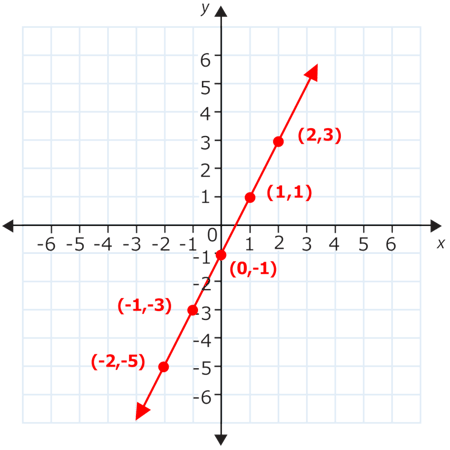
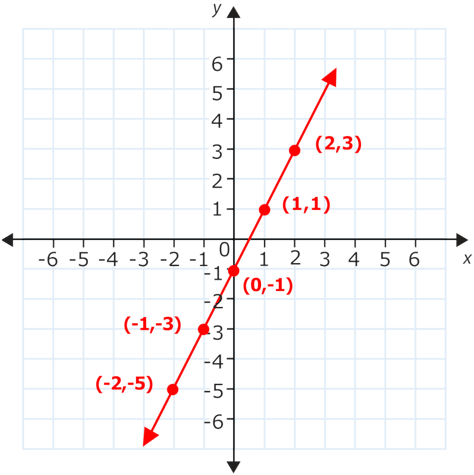
  ::首先,使用方程式来为函数创建表格并找到多个有顺序的对。使用一些负 x 值、一些正 x 值和 0,这是一个好主意。例如,您可以创建一个表格,在 x 等于 - 2, - 1, 0, 1, 和 2 时查找 y 值。

    $\begin{array}{r}y=2x-1\end{array}$

  $\begin{array}{r}x\end{array}$	$\begin{array}{r}y\end{array}$
  $\begin{array}{r}-2\end{array}$	$\begin{array}{r}-5\end{array}$	$\begin{array}{r}2(-2)-1=-5\end{array}$
  $\begin{array}{r}-1\end{array}$	$\begin{array}{r}-3\end{array}$	$\begin{array}{r}2(-1)-1=-3\end{array}$
  	$\begin{array}{r}-1\end{array}$	$\begin{array}{r}2(0)-1=-1\end{array}$
  $\begin{array}{r}1\end{array}$	$\begin{array}{r}1\end{array}$	$\begin{array}{r}2(1)-1=1\end{array}$
  $\begin{array}{r}2\end{array}$	$\begin{array}{r}3\end{array}$	$\begin{array}{r}2(2)-1=3\end{array}$

  播放段落

  The ordered pairs shown in the table are $\begin{array}{r}(-2,-5),(-1,-3),(0,-1),(1,1)\end{array}$  and $\begin{array}{r}(2,3)\end{array}$ .
  ::表中显示的有顺序配对是(-2,-5,(-1,-3,(0)-1,(1,1)和(2,3)。

  播放段落

  Plot those five points on the coordinate plane. Then connect them as shown below.
  ::在坐标平面上标出这五个点,然后将其连接如下:

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about Dana’s project, which was comparing the lengths and widths of caterpillars.
  ::更早之前, Dana 的项目给您带来了问题, 比较毛虫的长度和宽度。

  播放段落

  She’s put the data collected so far in a table (shown below). Can you plot these points and write the equation that models this information?
  ::她将迄今收集的数据放在一张表格中(如下表所示 ) 。 您能否绘制这些点和写出模拟这些信息的方程式?

  播放段落

  $$\begin{array}{r}\begin{array}{|cc|}\hline x\text{ (width in cm)}& y\text{ (length in cm)}\\ 2& 2\\ 3& 4\\ 4& 6\\ 5& 8\\ 6& 10\\ \hline\end{array}\end{array}$$

   
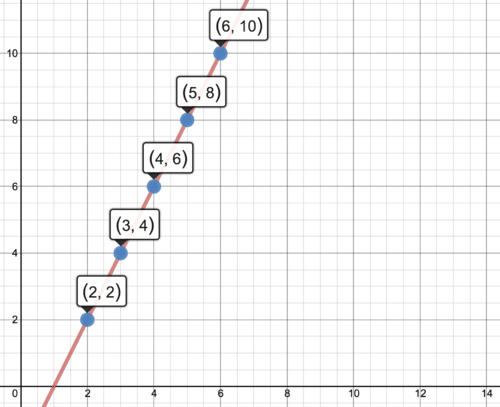
  First, represent this information as a set of ordered pairs so that you can plot the points $\begin{array}{r}\{(2,2),(3,4),(4,6),(5,8),(6,10)\}\end{array}$ .
  ::首先,将这些信息作为一组有顺序的对子表示,以便您能够绘制点 {(2),2,(3),(4),(6),(5),(8),(6),(10)}。

  播放段落

  Now, can you see a pattern in the table and then write the rule that describes it?
  ::现在,你能在表格中看到一个图案,然后写出描述它的规则吗?

  播放段落

  Notice that as $\begin{array}{r}x\end{array}$  increases by 1, $\begin{array}{r}y\end{array}$  increases by 2. So, you know that $\begin{array}{r}2x\end{array}$  is involved in the equation. But $\begin{array}{r}y\end{array}$  is not quite $\begin{array}{r}2x\end{array}$ . It is $\begin{array}{r}2x-2\end{array}$ .
  ::注意当 x 增加 1 y 增加 2 。 所以, 您知道 2x 包含在方程中 。 但是 y 不是 相当 2x 。 它是 2x-2 。

  播放段落

  So the equation that models this information is $\begin{array}{r}2x-2\end{array}$ .
  ::因此,这种信息模型的方程式是 2x-2 。

  播放段落

  Next, plot the points on the coordinate plane and draw a line through them. The graph is shown below.
  ::接下来,绘制坐标平面上的点,然后通过它们绘制一条线条。图示如下。

  

  播放段落

  Example 2
  ::例2

  播放段落

  The table below represents inputs and outputs of a linear function. Can you represent this information as ordered pairs, figure out the equation for this function, and then graph the function?
  ::下表显示线性函数的输入和输出。您能否以定购对对表示此信息, 找出此函数的方程式, 然后绘制函数图 ?

  播放段落

  $$\begin{array}{r}\begin{array}{|cc|}\hline x& y\\ 1& 5\\ 2& 10\\ 3& 15\\ 4& 20\\ \hline\end{array}\end{array}$$

  
  ::xy15210315420

  播放段落

  You can extract information from the table and represent the same information as a set of ordered pairs. The $\begin{array}{r}x\end{array}$ -coordinate is the first value and the $\begin{array}{r}y\end{array}$ -coordinate is the second value.
  ::您可以从表格中提取信息,并代表与一组定购对对相同的信息。 x 坐标是第一个值, Y 坐标是第二个值。

  $$\begin{array}{r}\{(1,5),(2,10),(3,15),(4,20)\}\end{array}$$

  播放段落

  Next, looking at the information in the table, you can see that when you multiply the $\begin{array}{r}x\end{array}$ -value by 5 you get the $\begin{array}{r}y\end{array}$ -value. The rule is multiply $\begin{array}{r}x\end{array}$  by 5 to get $\begin{array}{r}y\end{array}$ . You can write this as an equation.
  ::接下来,看看表格中的信息,你可以看到,当乘以 X 值乘以 5 时,你就会得到 Y 值。规则是乘以 x 乘以 5 以 y。你可以将此写成一个方程。

  播放段落

  $$\begin{array}{r}y=5x\end{array}$$

  
  ::y=5x y=5x

  播放段落

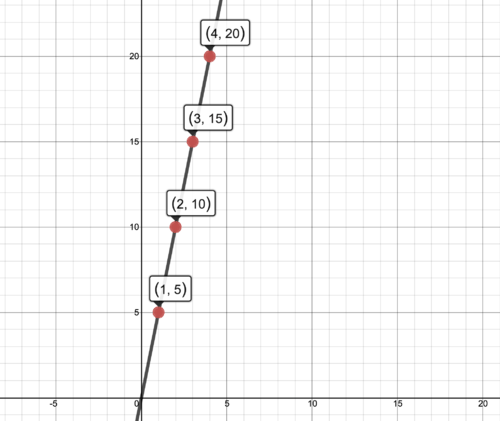
  You can graph plot the coordinates $\begin{array}{r}\{(1,5),(2,10),(3,15),(4,20)\}\end{array}$  and draw a line through them to see the graph.
  ::您可以绘制坐标 {(1, 5, (2, 10), (3, 15), (4, 20)) 并绘制一条线以查看图表 。

  

  播放段落

  Answer the following questions about functions and coordinates.
  ::回答下列关于职能和坐标的问题。

  播放段落

  Example 3
  ::例3

  

  播放段落

  Is the function above increasing or decreasing?
  ::职能高于增加还是减少?

  播放段落

  Notice that as $\begin{array}{r}x\end{array}$  increases $\begin{array}{r}y\end{array}$  increases. Notice that every time you increase $\begin{array}{r}x\end{array}$  by 1, $\begin{array}{r}y\end{array}$  will always increase. In this case, $\begin{array}{r}y\end{array}$  increases by two every time $\begin{array}{r}x\end{array}$  increases by 1.
  ::注意 x 增加 y 增加 y 增加 。 注意每次增加 x 1, y 总是增加 。 在这种情况下, y 每次增加 1 增加 2 y 增加 。

  播放段落

  The answer is the function is increasing.
  ::答案是功能正在增加。

  播放段落

  Example 4
  ::例4

  播放段落

  In the point $\begin{array}{r}(-3,4)\end{array}$  is the $\begin{array}{r}x\end{array}$ -value positive or negative?
  ::在点(-3,4)中,X值是正值还是负值?

  播放段落

  The $\begin{array}{r}x\end{array}$ -value is the first value in the coordinate. It is a negative number.
  ::x 值是坐标的第一个值。 这是一个负数 。

  播放段落

  The answer is the $\begin{array}{r}x\end{array}$ -value is negative.
  ::答案是x值为负值。

  播放段落

  Example 5
  ::例5

  播放段落

  In $\begin{array}{r}(-6,-7)\end{array}$ , which value is $\begin{array}{r}y\end{array}$ -value?
  ::在(-6,-7)中,什么值是Y值?

  播放段落

  The $\begin{array}{r}y\end{array}$ -value is the second value in a coordinate, and it is equal to -7.
  ::Y值是坐标中的第二个值,等于-7。

  播放段落

  The answer is the $\begin{array}{r}y\end{array}$ -value is -7.
  ::答案是Y值是 -7

  播放段落

  Review
  ::回顾

  播放段落

  The information in the table represents points from a linear function. Plot the points in the table on a coordinate plane, and then draw a straight line through them to graph each function. Then identify the rule (equation) for the function.
  ::表格中的信息代表线性函数的点。在坐标平面上绘制表格中的点,然后通过它们绘制一条直线以图示每个函数。然后为函数指定规则(等距)。

  1.   

  Input	Output
  1	4
  2	5
  3	6
  4	7

  2.   

  Input	Output
  2	4
  3	6
  4	8
  5	10

  3.   

  Input	Output
  1	3
  2	6
  4	12
  5	15

  4.   

  Input	Output
  9	7
  7	5
  5	3
  3	1

  5.   

  Input	Output
  8	12
  9	13
  11	15
  20	24

  6.   

  Input	Output
  3	21
  4	28
  6	42
  8	56

  7.   

  Input	Output
  2	5
  3	7
  4	9
  5	11

  8.  

  Input	Output
  4	7
  5	9
  6	11
  8	15

  9.   

  Input	Output
  5	14
  6	17
  7	20
  8	23

  10.   

  Input	Output
  4	16
  5	20
  6	24
  8	32

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源