Course: 9.8 利用毕达哥里定理解决等式

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 利用毕达哥里定理解决等式

Collapse Expand
利用毕达哥里定理解决等式
Gary wants to build a skateboard ramp, but it can’t be too steep. If he has a platform 3 m high and a board 5 m long, how far out should the board extend from the platform?
::Gary想建造滑板坡,但不会太陡峭。如果他有一个高3米高的平台和一个5米长的板,董事会应该从平台延伸到多远?

In this concept, you will learn how to solve equations using the Pythagorean Theorem .
::在这个概念中,你将学会如何用毕达哥伦理论解析方程式。

Solving Equations Using the Pythagorean Theorem
::利用毕达哥里定理解决等式

The Pythagorean Theorem states that the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse . In a math sentence, where $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ are the legs and $\begin{aligned} c \end{aligned}$ is the hypotenuse, it looks like this:
::Pytagorean Theorem指出,右三角形两腿的平方和等于下限的平方。在数学句中,a和b是双腿,c是下限,它看起来是这样的:

$\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}$
::c2=a2+b2 (千兆赫)

Mathematically, you can use this equation to solve for any of the variables, not just the hypotenuse.
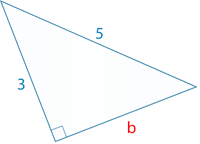
::从数学角度来说,你可以用这个方程来解决任何变量,而不仅仅是下限。

For example, the right triangle below has one leg equal to 3 and a hypotenuse of 5.
::例如,下方右三角形的一条腿等于3,低于5。

Solve for the other leg.
::解决另一条腿。

First, you can label either leg $\begin{aligned} a \end{aligned}$ or $\begin{aligned} b \end{aligned}$ . Remember that the legs are those sides adjacent to the right angle.
::首先,您可以标为腿 a 或 b。记住, 腿是右角的侧面。

Next, fill into the Pythagorean Theorem the values that you know.
::接下来,向毕达哥里安神话中填充你所知道的值。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ 5^{2} & = & 3^{2} + b^{2} \end{array} \end{aligned}$

::c2=a2+b252=32+b2

Then, perform the calculations you are able to.
::然后按照你的能力进行计算

$\begin{aligned} 25 = 9 + b^{2} \end{aligned}$
::25=9+b2 25=9+b2

Remember that your goal is to isolate the unknown variable on one side of the equation. In this case it is $\begin{aligned} b \end{aligned}$ and it is attached to a square and $\begin{aligned} a + 9 \end{aligned}$ . Perform the necessary operations to isolate $\begin{aligned} b \end{aligned}$ .
::记住您的目标是在方程的一面分离未知变量。在这种情况下,它是 b, 并且它附属于一个正方形和一个+ 9 。执行分离 b 的必要操作。

$\begin{aligned} \begin{array}{rcl} 25 - 9 & = & 9 + b^{2} - 9 \\ 16 & = & b^{2} \\ 4 & = & b \end{array} \end{aligned}$
The answer is 4.
::25-9=9+b2-916=b24=b4 回答是4

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Gary and his skate board ramp.
::早些时候,你得到一个问题关于加里和他的滑板斜坡。

One side, the base, was 4 m and the board, the hypotenuse, was 5 m. How high would the ramp be?
::一面是基底,4米, 板,下层,5米。坡道有多高?

First, substitute .
::第一,替代。

$\begin{aligned} 5^{2} = 3^{2} + b^{2} \end{aligned}$
::52=32+b2

Next, perform the calculations.
::接下来,进行计算。

$\begin{aligned} \begin{array}{rcl} 25 & = & 9 + b^{2} \\ 25 - 9 & = & 9 + b^{2} - 9 \end{array} \end{aligned}$

::25=9+b225-9=9+b2-9

Then, determine the square roots.
::然后,决定平方根。

$\begin{aligned} \begin{array}{rcl} 16 & = & b^{2} \\ 4 & = & b \end{array} \end{aligned}$

::16=b24=b

The answer is 4 m. Gary’s board should extend 4 m from the base of the platform.
::答案是4米。 Gary的董事会应该从平台底部4米宽。

Example 2
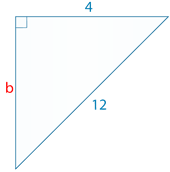
::例2

Solve for $\begin{aligned} b \end{aligned}$ to the nearest tenth.
::解决b到最近的十分之一。

First, take the given lengths and substitute them into the formula .
$\begin{aligned} \begin{array}{rcl} 4^{2} + b^{2} = 12^{2} \\ 16 + b^{2} = 144 \end{array} \end{aligned}$
Next, subtract 16 from both sides of the equation.
::首先,将给定长度取以给定长度并将其替换为公式。 42+b2=12216+b2=144 下一个,从方程两侧减去16。

$\begin{aligned} \begin{array}{rcl} 16 - 16 + b^{2} & = & 144 - 16 \\ b^{2} & = & 128 \end{array} \end{aligned}$

Then take the square root of both sides of the equation.
::16-16+b2=144-16b2=128 然后取方程两侧的平方根。

$\begin{aligned} b = 11.3137085 \dots \end{aligned}$
::b=11.3137085... =11.3137085...

Round to the tenths place
::回合到十分位

$\begin{aligned} b \approx 11.3 \end{aligned}$
::11.3

The answer is 11.3
::答案是11.3

Example 3
::例3

A right triangle includes the dimensions of $\begin{aligned} a \end{aligned}$ , $\begin{aligned} b = 6 \end{aligned}$ and $\begin{aligned} c = 13 \end{aligned}$ . Solve for $\begin{aligned} a \end{aligned}$ .
::右三角形包含 a, b=6 和 c=13 的尺寸。解决 a 。

First, substitute.
::第一,替代。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ 13^{2} & = & a^{2} + 6^{2} \end{array} \end{aligned}$

::c2=a2+b2132=a2+62

Next, perform the calculations you are able to.
::下一步, 执行您能够完成的计算。

$\begin{aligned} \begin{array}{rcl} 169 & = & a^{2} + 36 \\ 169 - 36 & = & a^{2} + 36 - 36 \end{array} \end{aligned}$

::169=a2+36169-36=a2+36-36

Then, determine the square roots.
$\begin{aligned} \begin{array}{rcl} 133 & = & a^{2} \\ 11.532582594 \dots & = & a \\ 11.5 & \approx & a \end{array} \end{aligned}$

::然后确定平方根 133=a211.532582594...=a11.5a

The answer is $\begin{aligned} a = 11.5 \end{aligned}$
::答案是a=11.5

Example 4
::例4

A right triangle with $\begin{aligned} a = 8, b \end{aligned}$ , and $\begin{aligned} c = 12 \end{aligned}$
::a=8,b和c=12的右三角形

First, substitute.
::第一,替代。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ 12^{2} & = & 8^{2} + b^{2} \end{array} \end{aligned}$
Next, perform the calculations.
::c2=a2+b2122=82+b2 下一个,进行计算。

$\begin{aligned} \begin{array}{rcl} 144 & = & 64 + b^{2} \\ 144 - 64 & = & 64 + b^{2} - 64 \end{array} \end{aligned}$

::144=64+b2144-64=64+b2-64

Then, determine the square roots.
::然后,决定平方根。

$\begin{aligned} \begin{array}{rcl} 80 & = & b^{2} \\ 8.9 & \approx & b \end{array} \end{aligned}$

::80=b28.9b

The answer is 8.9
::答案是8.9

Example 5
::例5

A right triangle with $\begin{aligned} a = 6 \end{aligned}$ , $\begin{aligned} b \end{aligned}$ , and $\begin{aligned} c = 10 \end{aligned}$
::a=6、b和c=10的右三角形

First, substitute.
::第一,替代。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ 10^{2} & = & 6^{2} + b^{2} \end{array} \end{aligned}$

::c2=a2+b2102=62+b2

Next, perform the calculations.
::接下来,进行计算。

$\begin{aligned} \begin{array}{rcl} 100 & = & 36 + b^{2} \\ 100 - 36 & = & 36 + b^{2} - 36 \end{array} \end{aligned}$

::100=36+b2100-36=36+b2-36

Then, determine the square roots.
::然后,决定平方根。

$\begin{aligned} \begin{array}{rcl} 64 & = & b^{2} \\ 8 & = & b \end{array} \end{aligned}$

::64=b28=b

The answer is 8.
::答案是8岁

Review
::回顾

Use the Pythagorean Theorem to find the length of each missing leg. You may round to the nearest tenth when necessary.
::使用毕达哥里安定理词查找每条缺失腿的长度。必要时您可以绕到最近的第十条。

$\begin{aligned} a = 6, b = ?, c = 12 \end{aligned}$
::a=6,b=? c=12

$\begin{aligned} a = 9, b = ?, c = 15 \end{aligned}$
::a=9,b=? c=15

$\begin{aligned} a = 4, b = ?, c = 5 \end{aligned}$
::a=4,b=4,b=? c=5

$\begin{aligned} a = 9, b = ?, c = 18 \end{aligned}$
::a=9,b=? c=18

$\begin{aligned} a = 15, b = ?, c = 25 \end{aligned}$
::a=15,b=? c=25

$\begin{aligned} a = ?, b = 10, c = 12 \end{aligned}$
::a=? b=10 c=12

$\begin{aligned} a = ?, b = 11, c = 14 \end{aligned}$
::a=? b=11 c=14

$\begin{aligned} a = ?, b = 13, c = 15 \end{aligned}$
::a=? b=13 c=15

Write an equation using the Pythagorean Theorem and solve each problem. Round to the nearest tenth when necessary.
::使用 Pythagorena 理论书写方程式, 并解决每个问题。必要时, 圆到最近的十分。

Joanna laid a plank of wood down to make a ramp so that she could roll a wheelbarrow over a low wall in her garden. The wall is 1.5 meters tall, and the plank of wood touches the ground 2 meters from the wall. How long is the wooden plank?
::乔安娜把木板放下来做一个斜坡,这样她就可以把一把手推车翻过花园的低墙壁。墙长1.5米,木板与墙边两米处的地面相接。木板有多长?

Write the equation.
::写出方程式

Solve for the answer.
::解决答案。

Chris rode his bike 4 miles west and then 3 miles south. What is the shortest distance he can ride back to the point where he started?
::克里斯骑着自行车往西4英里,然后往南3英里。

Write the equation.
::写出方程式

Solve the problem.
::解决问题

Naomi is cutting triangular patches to make a quilt. Each has a diagonal side of 14.5 inches and a short side of 5.5 inches. What is the length of the third side of each triangular patch?
::Naomi 正在切开三角形的补丁来做一个缝隙。每人有14.5英寸的对角面和5. 5英寸的短边。每个三角形的第三边的长度是多少?

Write the equation.
::写出方程式

Solve the problem.
::解决问题

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

General

利用毕达哥里定理解决等式

Solving Equations Using the Pythagorean Theorem ::利用毕达哥里定理解决等式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Solving Equations Using the Pythagorean Theorem
::利用毕达哥里定理解决等式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源