12.10 基本计算规则

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 基本计算规则

  Collapse Expand

  基本计算规则

  

  播放段落

  Brian is going shopping for new blue jeans.  He has many options from which to choose.  For fit, he can choose skinny, boot cut, or flare.  For wash, he can choose dark, faded, or distressed.  For rise, he can choose low rise or regular.  How many different options does Brian have?
  ::布赖恩去买新的蓝色牛仔裤。 他有很多选择。 适合的话, 他可以选择瘦瘦、 靴子切割或照明弹。 用于洗涤, 他可以选择黑暗、 淡化或痛苦。 对于升起, 他可以选择低升或常规。 布莱恩可以选择多少不同的选择?

  播放段落

  In this concept, you will learn how to use the Counting Principle to calculate the total possible outcomes of a series of events.
  ::在这个概念中,你将学会如何使用计算原则来计算一系列事件可能的总结果。

  播放段落

  The Counting Principle
  ::计算原则

  播放段落

  provide you with a visual way of seeing all of the possible outcomes for a set of particular events.  But it requires quite a bit of effort.  What if there was a simpler way?  You can use another principle to figure out the possible outcomes.
  ::给您提供一个视觉方式, 查看一系列特定事件的所有可能结果。 但是这需要相当的努力。 如果有一个简单的方法呢? 您可以使用另一个原则来找出可能的结果 。

  播放段落

  Let's look at an example:
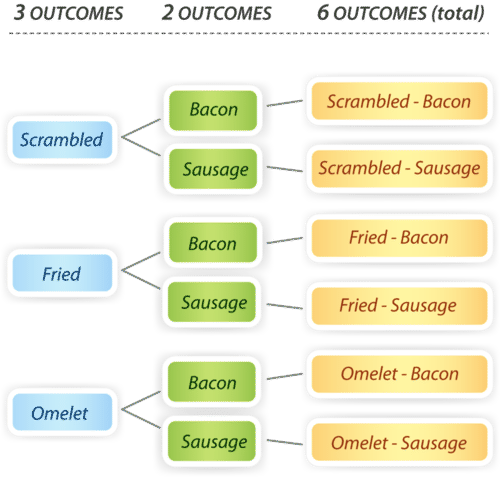
  ::让我们举个例子:

  播放段落

  Molly’s All Star Farm Breakfast features 3 choices of eggs–scrambled, fried, or omelet–plus a choice of bacon or sausage. You can use a tree diagram to find that there are 6 different choices, or outcomes, for the breakfast.
  ::Molly的《全星农场早餐 》 ( All Star Farm Mreedom)有三个鸡蛋选择 — — 鸡蛋、煎蛋或煎蛋 — — 加上培根或香肠选择。 你可以用树图来发现早餐有6种不同的选择或结果。

  

  播放段落

  To look at this another way, you could look at the number of possible breakfast options in terms of outcomes.
  ::以另一种方式来看,你可以从结果的角度来看待可能的早餐选择的数量。

  播放段落

  For the first choice there are 3 different outcomes. For the second choice there are 2 different outcomes.
  ::第一种选择有三种不同的结果,第二种选择有两种不同的结果。

  播放段落

  $\begin{array}{r}3\text{outcomes}\cdot 2\text{outcomes}=6\text{outcomes}\end{array}$
  ::3成果2成果=6成果

  播放段落

  The Counting Principle is a rule to figure out the total possible outcomes of a series of events.  The Counting Principle for the number of choices or outcomes for two , $\begin{array}{r}A\end{array}$ and $\begin{array}{r}B\end{array}$ taken together, is the product of the total number of outcomes for each event .
  ::《计算原则》是一项规则,用以确定一系列活动的可能总结果。 A 和 B 两者的选择或结果数的计算原则是每项活动结果总数的结果。

  播放段落

  Total outcomes for $\begin{array}{r}A\end{array}$ and $\begin{array}{r}B=(\text{number of outcomes for}A)\cdot (\text{number of outcomes for}B)\end{array}$
  ::A和B的总结果合计=(A结果数目)___________________(B结果数目)

  播放段落

  The Counting Principle will work for 2, 3 even 4 different events. 
  ::计数原则将适用于2、3、甚至4个不同事件。

  播放段落

  Here is another example:
  ::以下是另一个例子:

  播放段落

  For buying gum you have the following choices:
  ::对于购买口香糖,您有以下选择:

  播放段落
  • 3 flavor choices–spearmint, peppermint, cinnamon
    ::3种口味选择 - 香肠、薄荷、肉桂
  播放段落
  • 2 sugarless choices–sugarless or non-sugarless
    ::2个无糖选择 — — 无糖或无糖 — — 无糖或无糖
  播放段落
  • 2 bubble choices–bubble gum or regular
    ::2个泡沫选项 - 泡沫口香糖或普通

  播放段落

  $$\begin{array}{r}3\text{choices}\cdot 2\text{choices}\cdot 2\text{choices}=12\text{choices}\end{array}$$

  
  ::选择3=2 选择2=12 选择

  播放段落

  To check the answer, write out all of the possible options for gum:
  ::要检查答案, 请写出所有可能的口香糖选项 :

  播放段落

  $$\begin{array}{rlrlrl}& \text{spear-sugarless-bubble}& & \text{pepper-sugarless-bubble}& & \text{cinnamon-sugarless-bubble}\\ & \text{spear-sugarless-regular}& & \text{pepper-sugarless-regular}& & \text{cinnamon-sugarless-}\\ & \text{spear-non-bubble}& & \text{pepper-non-bubble}& & \text{regular}\\ & \text{spear-non-regular}& & \text{pepper-non-regular}& & \text{cinnamon-non-bubble}\\ & & & & & \text{cinnamon-non-regular}\end{array}$$

  
  ::长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 长矛 - 无长矛 - 无长矛 - 无长矛 - 长矛 - 无长矛 - 无长矛 - 无长矛 - 长矛 - 长矛 - 无长矛 - 长矛 - 无长矛 - 长矛 - 长矛 - 无长矛 - 长矛 - 无长矛 - 无长矛 - 无长

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about Brian's blue jean shopping expedition.
  ::早些时候,你得到一个问题 关于布莱恩的蓝豆购物探险。

  播放段落

  He has a number of possible options which include fit:  skinny, boot cut, or flare; wash:  dark, faded, distressed; and rise:  low or regular.  How many possible choices of blue jeans does Brian have?
  ::他有若干可能的选择,包括合适的选择:瘦、靴子切割或照明弹;洗:黑暗、淡化、痛苦;上升:低或定期。 Brian有多少可能选择蓝色牛仔裤?

  播放段落

  First, count the number of possibilities for each option:
  ::首先,计算每个选项的可能性数量:

  播放段落

  Fit:  3
  ::适合:3

  播放段落

  Wash:  3
  ::洗涤:3

  播放段落

  Rise:  2
  ::崛起:2

  播放段落

  Next, use the Counting Principles method of calculating total outcomes:
  ::其次,使用计算原则方法计算总结果:

  播放段落

  $$\begin{array}{r}3\text{choices}\cdot 3\text{choices}\cdot 2\text{choices}=18\text{choices}\end{array}$$

  
  ::3#3%3%2选择=18选择

  播放段落

  Then, record your answer as total possible outcomes.
  ::然后,记录你的答复 可能的全部结果。

  播放段落

  The answer is Brian has 18 choices of blue jeans from which to choose.
  ::答案是布莱恩有18种选择 蓝牛仔裤可供选择

  播放段落

  Example 2
  ::例2

  播放段落

  You’re buying a sweater and have the following choices.  
  ::您正在购买一件毛衣, 并有以下选择。

  播放段落
  • Color choices–black, yellow, blue, red, green
    ::颜色选择 - 黑色、 黄色、 蓝色、 蓝色、 红色、 绿色
  播放段落
  • Material choices–wool, cotton, fleece
    ::材料选择 -- -- 腰、棉花、羊毛
  播放段落
  • Style choices–v-neck, crew, button-down, turtle
    ::样式选择 -v - neck, 船员, 扣下按钮, 乌龟

  播放段落

  How many sweater possibilities do you have?
  ::你有多少毛衣的可能性?

  播放段落

  First, count the number of each different choice:
  ::首先,计算每个不同选择的数目:

  播放段落

  Color choices:  5
  ::颜色选择: 5

  播放段落

  Material choices:  3
  ::材料选择:3

  播放段落

  Style choices:  4
  ::样式选择: 4

  播放段落

  Next, use the Counting Principles method of calculating total outcomes:
  ::其次,使用计算原则方法计算总结果:

  播放段落

  $$\begin{array}{r}5\text{choices}\cdot 3\text{choices}\cdot 4\text{choices}=60\text{choices}\end{array}$$

  
  ::5%3%4选择=60选择

  播放段落

  Then, record your answer as total possible outcomes.
  ::然后,记录你的答复 可能的全部结果。

  播放段落

  The answer is you have 60 choices of sweaters from which to choose.
  ::答案是,你有60种毛衣可供选择。

  播放段落

  Example 3
  ::例3

  播放段落

  Omar is buying a skateboard. He has 5 different skateboard decks to choose from and 4 different wheel choices. How many different skateboard choices does Omar have?
  ::Omar正在购买一个滑板。他有5个不同的滑板甲板可以选择,4个不同的轮子。Omar有多少不同的滑板?

  播放段落

  First, count the number of each different choice:
  ::首先,计算每个不同选择的数目:

  播放段落

  Decks:  5
  ::马克: 5

  播放段落

  Wheels:  4
  ::轮轮:4轮

  播放段落

  Next, use the Counting Principles method of calculating total outcomes:
  ::其次,使用计算原则方法计算总结果:

  播放段落

  $$\begin{array}{r}5\text{choices}\cdot 4\text{choices}=20\text{choices}\end{array}$$

  
  ::5%4 选项=20 选项

  播放段落

  Then, record your answer as total possible outcomes.
  ::然后,记录你的答复 可能的全部结果。

  播放段落

  The answer is Omar has 20 different skateboard choices.
  ::答案是奥马尔有20种不同的滑板选择

  播放段落

  Example 4
  ::例4

  播放段落

  Ice Stone ice cream shop has 3 different sundae sizes: baby, large, and grand. You can choose from 6 different ice cream flavors and add 4 different toppings. How many sundae choices are there?
  ::冰冰冰淇淋店有3种不同的圣代大小:婴儿、大、大。你可以从6种不同的冰淇淋口味中选择6种不同的冰淇淋,再加4种不同的托普。有多少个圣代的选择?

  播放段落

  First, count the number of each different choice:
  ::首先,计算每个不同选择的数目:

  播放段落

  Size:  3
  ::规模:3

  播放段落

  Flavors:  6
  ::平价:6

  播放段落

  Toppings:  4
  ::拖网:4

  播放段落

  Next, use the Counting Principles method of calculating total outcomes:
  ::其次,使用计算原则方法计算总结果:

  播放段落

  $$\begin{array}{r}3\text{choices}\cdot 6\text{choices}\cdot 4\text{choices}=72\text{choices}\end{array}$$

  
  ::3#6%4选择=72选择

  播放段落

  Then, record your answer as total possible outcomes.
  ::然后,记录你的答复 可能的全部结果。

  播放段落

  The answer is you have 72 choices of sundaes.
  ::答案就是你有72种圣代的选择

  播放段落

  Example 5
  ::例5

  播放段落

  Gina tosses a number cube 2 times. How many different outcomes are there?
  ::吉娜扔了2倍的立方体 有多少不同的结果?

  播放段落

  First, count the number of each different choice:
  ::首先,计算每个不同选择的数目:

  播放段落

  Number choices:  6
  ::数字选择:6

  播放段落

  Number of rolls:  2
  ::卷数数:2

  播放段落

  Next, use the Counting Principles method of calculating total outcomes:
  ::其次,使用计算原则方法计算总结果:

  播放段落

  $$\begin{array}{r}6\text{choices}\cdot 2\text{rolls}=12\text{outcomes}\end{array}$$

  
  ::6#2 卷=12 结果

  播放段落

  Then, record your answer as total possible outcomes.
  ::然后,记录你的答复 可能的全部结果。

  播放段落

  The answer is there are 12 outcomes.
  ::答案是,有12个结果。

  播放段落

  Review
  ::回顾

  播放段落

  Use the Counting Principle to solve each problem.
  ::使用计算原则解决每个问题。

  播放段落
  1. The Cubs have 3 games left to play this year. How many different outcomes can there be for the three games?
     ::小熊队今年还有3场比赛要玩。这3场比赛能有多少不同的结果?
  播放段落
  2. Svetlana tosses a coin 4 times in a row. How many outcomes are there for the 4 tosses?
     ::Svetlana 连续4次抛硬币。 4个硬币有多少结果?
  播放段落
  3. For a new tennis racquet, Danny can choose from 8 different brands, 3 different head sizes, and 4 different grip sizes. How many different racquet choices does Danny have?
     ::对于新的网球场来说,Danny可以选择8个不同的品牌,3个不同的头大小,4个不同的控制大小。 Danny可以选择多少个不同的球场?
  播放段落
  4. Gina tosses a number cube 3 times. How many different outcomes are possible?
     ::Gina三次抛出一个数字立方体 有多少不同的结果?
  播放段落
  5. Gina tosses a number cube. Buster flips a coin. How many different outcomes are possible for the two events?
     ::吉娜抛出一个数字立方体。 Buster翻了一个硬币。 这两场活动可以产生多少不同的结果?
  播放段落
  6. Buster flips a coin. Daoud chooses a card from a deck of 52 cards. How many different outcomes are possible for the two events?
     ::巴斯特翻硬币。 Daoud 从52张牌牌的牌牌牌中选择一张牌。 这两场比赛可以取得多少不同的结果?
  播放段落
  7. Rex spins a spinner that has red, blue, and yellow sections two times. How many different outcomes are possible?
     ::Rex 旋转一个红色、 蓝色 和 黄色 段的旋转器, 旋转两次 。 有多少不同的结果可能发生 ?
  播放段落
  8. Daoud chooses a card from a deck of 52 cards, replaces the card in the deck, then chooses a second card. How many different outcomes are possible?
     ::Daoud 从52张牌牌的牌牌中选择一张牌, 替换牌牌中的牌, 然后选择第二张牌。 有多少不同的结果是可能的?
  播放段落
  9. Patsy’s Pizza features 3 different pizza types, 14 different toppings, and 2 different sizes. How many different pizzas can you order?
     ::Patsy的披萨有3种不同的披萨,14种不同的托普和2种不同的尺寸。 你能订购多少种不同的披萨?
  播放段落
  10. Spud has a 2-letter password for his computer using letters only. If there are 26 different letters in the alphabet, how many different passwords are possible?
      ::Spud的计算机有2个字母密码,只使用字母。如果字母表中有26个不同的字母,那么可以使用多少个不同的密码?
  播放段落
  11. Doreen has a 3-digit password for her computer using digits only. If there are 10 different digits (including zero), how many different passwords are possible?
      ::Doreen的计算机有一个3位数密码, 仅使用数字。 如果有 10 位数( 包括零位数) , 那么有多少个密码是可能的 ?
  播放段落
  12. Sebastian has a 3-letter password for his computer using vowels (A, E, O, I, U) only. How many different passwords are possible?
      ::塞巴斯蒂安的电脑有3个字母密码,只能使用元音(A、E、O、I、U)。可以使用多少个不同的密码?
  播放段落
  13. If Sebastian had a two - letter password, how many different passwords are possible?
      ::如果Sebastian有一个两个字母密码, 多少不同的密码是可能的?
  播放段落
  14. If Sebastian had a four - letter password, how many different passwords are possible?
      ::如果Sebastian有四个字母密码 有多少不同的密码?
  播放段落
  15. If Sebastian had a five - letter password, how many different passwords are possible?
      ::如果Sebastian有5个字母密码, 有多少不同的密码是可能的?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源