12.15 合并问题

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 合并问题

  Collapse Expand

  合并问题

  

  播放段落

  The ultimate Frisbee team just received their practice Frisbees. The Frisbees come in yellow, red, and blue. Marcos, the team captain, gives them out to the players two at a time. How many color combinations are possible?
  ::飞盘队刚收到他们练习的飞盘队 飞盘队是黄色、红色和蓝色的

  播放段落

  In this concept, you will learn how to calculate possible combinations.
  ::在这个概念中,你会学会如何计算可能的组合。

  播放段落

  Calculating Combinations
  ::计算组合

  播放段落

  Once you have determined that you are using combinations, it is necessary to count the combinations.
  ::一旦确定使用组合后,必须计算组合。

  播放段落

  There are several different ways to count combinations. When counting, try to keep the following in mind:
  ::计算组合有几种不同的方法。计算时,尽量铭记以下各点:

  播放段落
  • Go one by one through the items. Don’t stop your list until you’ve covered every possible link of one item to all other items.
    ::逐个浏览各个项目。 不要停止列表, 直到您把一个项目与所有其他项目的每一个可能的链接都覆盖在内 。
  播放段落
  • Keep in mind that order doesn’t matter. For combinations, there no difference between $\begin{array}{r}AB\end{array}$ and $\begin{array}{r}BA\end{array}$ . So if both $\begin{array}{r}AB\end{array}$ and $\begin{array}{r}BA\end{array}$ are on your list, cross one of the choices off your list.
    ::记住这个顺序并不重要。 对于组合来说,AB和BA之间没有区别。 所以如果AB和BA都列在你的名单上,请从你的列表中跳出一个选择。
  播放段落
  • Check your list for repeats. If you accidentally listed a more than once, cross the extra listings off your list.
    ::检查列表重复。 如果您不小心列出不止一次, 请从列表中跳过额外的列表 。

  播放段落

  James needs to choose a 2-color combination for his intramural team t-shirts. How many different 2-color combinations can James make out of red, blue, and yellow?
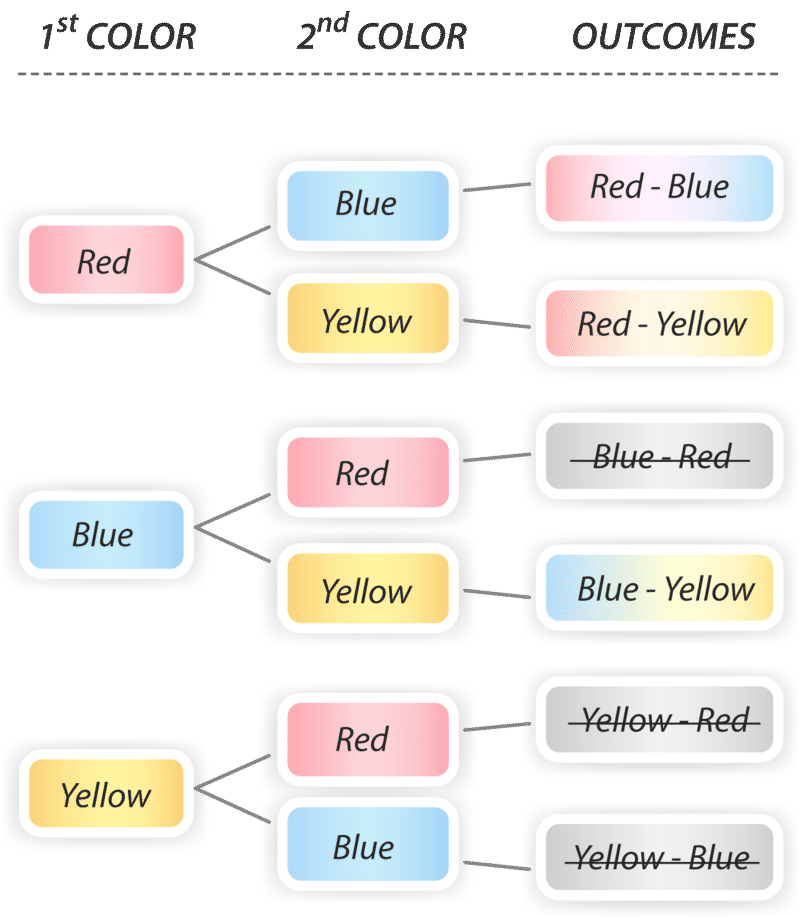
  ::James需要选择一个 2色的组合 来配配配他的内部团队T恤。James能用红色、蓝色和黄色 做多少不同的 2色组合?

  播放段落

  One way to find the number of combinations is to make a tree diagram . Here, if red is chosen as one color, that leaves only blue and yellow for the second color.
  ::找到组合数的一个方法就是绘制树图。 如果选择红色为一种颜色, 则第二个颜色只留下蓝色和黄色。

  

  播放段落

  The diagram shows all 6 permutations of the 3 colors. But we are counting combinations here, so order doesn’t matter.  Therefore, in this tree diagram, we will cross out all outcomes that are repeats. For example, the first red-blue is no different from blue-red, so we’ll cross out blue-red.  In all, there are 3 combinations that are not repeats.
  ::图表显示了这3种颜色的所有 6 个排列。 但我们在这里计算组合, 所以顺序并不重要 。 因此, 在这张树图中, 我们将交叉所有重复的结果。 比如, 第一个红色蓝与蓝色蓝没有区别, 所以我们会交叉蓝色红。 总共有3个组合不会重复。

  播放段落

  This method of making a tree diagram and crossing out repeats is reliable, but it is not the only way to find combinations.
  ::这种绘制树图和跨出重复数字的方法是可靠的,但这不是找到组合的唯一办法。

  播放段落

  Let's look at an example.
  ::让我们举个例子。

  播放段落

  James has added a fourth color, green, from which to choose in selecting a 2-color combination for his intramural team. How many different 2-color combinations can James make out of red, blue, yellow, and green?
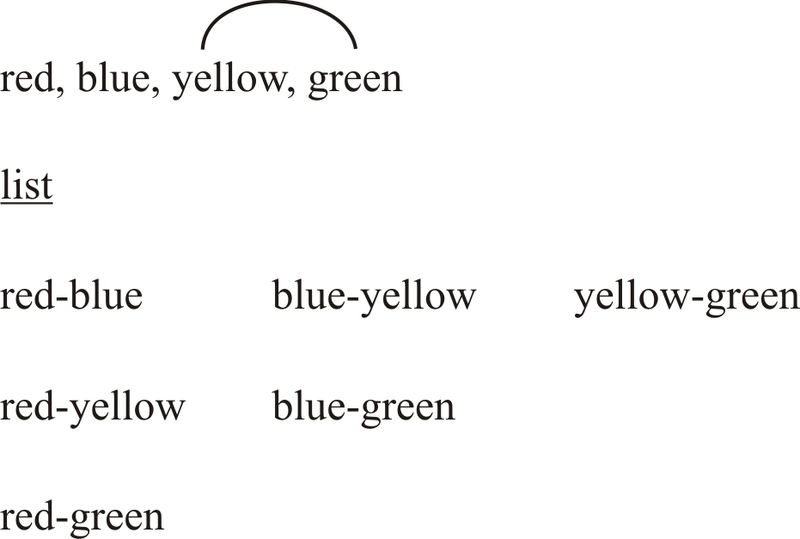
  ::James增加了第四个颜色,绿色,从中选择选择一个 2色组合,供他内部团队使用。James可以用红色、蓝色、黄色和绿色组合制成多少个不同的 2色组合?

  播放段落

  First, write the choices. Match the first choice, red, with the second, blue. Add the combination, red-blue, to your list. Match the other choices in turn. Add the combinations to your list.
  ::首先,写入选择。 匹配第一个选择, 红色, 与第二个选择匹配, 蓝色。 添加组合, 红色蓝色, 添加到列表中。 依次匹配其他选择。 将组合添加到列表中 。

  

  播放段落

  Next, move to the second choice, blue. Match blue up with every possible partner. Add the combinations to your list.
  ::下一步, 转到第二个选择, 蓝色 。 与每一个可能的伴侣匹配蓝色 。 将组合添加到您的列表中 。

  

  播放段落

  Then, move to the third choice, yellow. There is only one combination left to match it with. Add the combination to your list.
  ::然后,移到第三个选择, 黄色。 只有一个组合可以匹配它。 将组合添加到列表中 。

  

  播放段落

  The answer is there are 6 combinations.
  ::答案是6个组合。

  播放段落

  Sometimes, you won’t want to use all of the possible options in the combination. Think about it as if you have 16 flavors of ice cream, but you only want to use three flavors at a time. With an example like this one, you are looking for combinations of object where only a certain number of them are used in any one combination.  This happens a lot with teams.
  ::有时候,你不想在组合中使用所有可能的选项。 想象一下,你好像有16种冰淇淋的口味,但你只想要一次使用三种口味。 举例来说,你正在寻找只有一定数量的对象组合在任何一个组合中使用的组合。 这在团队中经常发生。

  播放段落

  Let's look at an example with teams.
  ::让我们看看一个团队的例子。

  播放段落

  How many different 2-player soccer teams can Jean, Dean, Francine, Lurleen, and Doreen form?
  ::Jean,Dean,Francine,Lurleen,和Doreen能组成多少不同的2人足球队?

  播放段落

  First, start with Jean. Add all combinations that begin with Jean to your list.
  ::首先,先从让开始,加上所有从让开始的组合。

  播放段落

  $$\begin{array}{rl}& \underset{\_}{\text{Combination}}\underset{\_}{\text{List}}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Dean}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Francine}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Doreen}\end{array}$$

  
  ::合并-List-Jean、Dean、Francine、Lurleen、Doreen-Jean-Dean、Dean、Francine、Lurleen、Doreen-Francine、Doreen-Francine、Dean、Francine、Lurleen、Doreen-Jean-Lurleen-Jean、Dean、Francine、Lurleen、Lurleen、Doreen-Jean-Doreen

  播放段落

  Next, go through all combinations that begin with Dean, Francine, and Lurleen.
  ::接下来,从迪安、弗朗辛和卢琳开始 研究所有的组合

  播放段落

  $$\begin{array}{rl}& \underset{\_}{\text{Combination}}\underset{\_}{\text{List}}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Dean}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Francine}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Dean-Francine}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Dean-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Dean-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Francine-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Francine-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Lurleen-Doreen}\end{array}$$

  
  ::合并名单:Jean、Dean、Francine、Lurleen、Lurleen、Doreen-Dea-Dean、Dean、Francine、Lurleen、Lurleen、Doreen-Frencine、Doreen-Lurleen-Lurleen-Jean、Dean、Francine、Francine、Francine、Lurleen、Doreen-Dean-Francine-Jean、Dean、Francine、Francine、Lurine、Lurleen、Doren、Doreen-Doreen-Doren-Jean、Dean、Francine、Lurleen、Doreen-Doreen、Dean、Francine、Lurleen、Doren-Doreen-Doreen、Dean、Francine、Lureen、Doren-Doren-Doren-Doren-Doreen、Dean、Francine、Lureen、Lureen、Lureen、Lureen、Lureen、Lureen、Dureen、Lureen-Doren-Doren-Doren-Doleen、Len、Len、De、De、De、Len、Lureen、Lureen、Lureen、Lureen、Len、Lureen、Lureen、Lureen、Len、Len、Lureen、Lureen、Len、Lurleen、Len、Lurleen、Len、Len、Len、Len、Len、Lurlen、Line、Line、Lurleen、Line、Lurleen、Lurleen、De、Len、Len、Len、Lurleen、Len、Len、Len、Len、Len、L、L、Len、Lurleen、Len、Len、Len、Len、Len、Len、Len、Len、Len、Len、Len、Len、Len、Len、Lurleen、Lurleen、Lurleen、De、De、De、Le、De、De、De、Len、Len、

  播放段落

  The answer is there are 10 combinations.
  ::答案是,有10个组合。

  播放段落

  Here is another example.
  ::下面是另一个例子。

  播放段落

  How many different 3-player soccer teams can Jean, Dean, Francine, Lurleen, and Doreen form?
  ::Jean,Dean,Francine,Lurleen,和Doreen能组成多少不同的3人足球队?

  播放段落

  First, start with Jean. Add all combinations that begin with Jean to your list.
  ::首先,先从让开始,加上所有从让开始的组合。

  播放段落

  Next, go through all combinations that begin with Dean, Francine, and Lurleen.
  ::接下来,从迪安、弗朗辛和卢琳开始 研究所有的组合

  播放段落

  $$\begin{array}{rl}& \underset{\_}{\text{Combination}}\underset{\_}{\text{List}}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Dean-Francine}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Dean-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Dean-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Francine-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Francine-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Jean-Lurleen-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Dean, Francine-Lurleen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Dean-Francine-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Dean-Lurleen-Doreen}\\ & \text{Jean, Dean, Francine, Lurleen, Doreen}\text{Francine-Lurleen-Doreen}\end{array}$$

  
  ::长者、长者、长者、弗朗辛、罗琳、罗琳、罗琳、多林、多林、多林、长者、弗朗辛、罗琳、多林、多林、多林、多林、多林、多林、多林、弗朗尼、弗朗尼、弗朗宁、多伦、多伦-弗朗-弗朗-里南-里昂-里昂-里昂、迪恩、弗朗、朗宁、多伦-里昂-里昂-里昂、迪恩、迪恩、弗朗尼、林-里昂、多林-里昂、林-里昂、林-里昂、林-里昂、林-里昂、林-里昂、林-里昂、林-里昂、林-里昂、林-里昂-里昂、林-里昂-里昂、林-里昂-里昂、迪昂-里昂-里昂、林-里昂-里昂、林-里昂-里昂、迪昂-里昂-里昂-里昂、

  播放段落

  The answer is there are 10 combinations.
  ::答案是,有10个组合。

  播放段落

  We can use a formula to help us to calculate combinations.
  ::我们可以用一个公式来帮助我们计算组合。

  播放段落

  Suppose you have 5 marbles in a bag–red, blue, yellow, green, and white. You want to know how many combinations there are if you take 3 marbles out of the bag all at the same time. In combination notation , you write this as:
  ::假设你有一个包里有五大理石, 红色, 蓝色, 黄色, 绿色, 白色。 你想知道如果同时从包里取出三大理石, 里面有多少组合。 在组合符号中, 你写为:

  播放段落

  $$\begin{array}{r}{}_5{C}_3⟸5\text{items taken 3 at a time}\end{array}$$

  
  ::5C3=5物项一次3件

  播放段落

  In general, combinations are written as:
  ::一般说来,组合的写法是:

  播放段落

  $$\begin{array}{r}{}_n{C}_r⟸n\text{items taken}r\text{at a time}\end{array}$$

  
  ::nCrn 项一次拍摄r

  播放段落

  To compute $\begin{array}{r}{}_n{C}_r\end{array}$ use the formula:
  ::要计算 nCr 使用公式:

  播放段落

  $$\begin{array}{r}{}_n{C}_r=\frac{n!}{r!(n-r)!}\end{array}$$

  
  ::Nrn! r! ! ! r! r! r! ! ! !

  播放段落

  where is the number of objects and (r) is the number taken at any one time.
  ::其中项为物体数目,(r)项为任一时间所用的数目。

  播放段落

  Now let’s look at applying the formula to the example.
  ::现在让我们来看看如何将公式应用到示例中。

  播放段落

  For $\begin{array}{r}{}_5{C}_3\end{array}$ :
  ::5C3:

  播放段落

  $$\begin{array}{r}{}_5{C}_3=\frac{5!}{3!(5-3)!}=\frac{5!}{3!2!}\end{array}$$

  
  ::5C3=5! 3! (5- 3) 5C3!2!

  播放段落

  Next, simplify.
  ::下一个,简化。

  播放段落

  $$\begin{array}{r}{}_5{C}_3=\frac{5(4)(3)(2)(1)}{(3\cdot 2\cdot 1)(2\cdot 1)}=\frac{120}{12}=10\end{array}$$

  
  ::5C3=5(4)(3)(2)(1)(1)(1)(3)(2)(1)(1)(2)(2)(2)(2)(2)(1)(2)(2)(1)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)=12012=10

  播放段落

  The answer is there are 10 possible combinations.
  ::答案是,有10种可能的组合。

  播放段落

  Here is another example.
  ::下面是另一个例子。

  播放段落

  Find $\begin{array}{r}{}_6{C}_2\end{array}$ .
  ::查找 6C2。

  播放段落

  First, understand what $\begin{array}{r}{}_6{C}_2\end{array}$ means.
  ::首先,明白6C2是什么意思。

  播放段落

  $$\begin{array}{r}{}_6{C}_2⟸6\text{items taken 2 at a time}\end{array}$$

  
  ::6C26物项一次取2件

  播放段落

  Next, set up the problem.
  ::下一个,设置问题。

  播放段落

  $$\begin{array}{r}{}_6{C}_2=\frac{6!}{2!(6-2)!}\end{array}$$

  
  ::6C2=6! 2! (6-2)!

  播放段落

  Then, fill in the numbers and simplify.
  ::然后,填满数字,简化。

  播放段落

  $$\begin{array}{r}{}_6{C}_2=\frac{6(5)(4)(3)(2)(1)}{(2\cdot 1)(4\cdot 3\cdot 2\cdot 1)}=\frac{720}{48}=15\end{array}$$

  
  ::6C2=6(5)(4)(3)(2)(1)(2)1(4321)=72048=15

  播放段落

  The answer is there are 15 possible combinations.
  ::答案是,有15种可能的组合。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about Marcos, who was handing out Frisbees to his teammates.  
  ::之前有人给你一个马科斯的问题 他把飞盘交给他的队友

  播放段落

  He is handing them out 2 at a time and there are three colors:  yellow, red, and blue.  How many color combinations are possible?
  ::他一次拿出两个颜色,有三种颜色:黄色、红色和蓝色。有多少种颜色组合是可能的?

  播放段落

  First, understand what  $\begin{array}{r}{}_3{C}_2\end{array}$  means.
  ::首先,理解3C2是什么意思。

  播放段落

  $$\begin{array}{r}{}_3{C}_2⟸3\text{items taken 2 at a time}\end{array}$$

  
  ::3C2QQ3 项一次取 2 项 。

  播放段落

  Next, set up the problem.
  ::下一个,设置问题。

  播放段落

  $$\begin{array}{r}{}_3{C}_2=\frac{3!}{2!(3-2)!}\end{array}$$

  
  ::3C2=3! 2! (3 -2)!

  播放段落

  Then, fill in the numbers and simplify.
  ::然后,填满数字,简化。

  播放段落

  $$\begin{array}{r}{}_3{C}_2=\frac{(3)(2)(1)}{(2\cdot 1)(1)}=\frac{6}{2}=3\end{array}$$

  
  ::3C2=(3)(2)(2)(1)([1](1)=62=3

  播放段落

  The answer is there are 3 possible color combinations of Frisbees.
  ::答案是Frisbees有三种可能的颜色组合。

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{array}{r}{}_5{C}_4\end{array}$
  ::5C4 5C4

  播放段落

  First, understand what  $\begin{array}{r}{}_5{C}_4\end{array}$  means.
  ::首先,明白5C4是什么意思。

  播放段落

  $$\begin{array}{r}{}_5{C}_4⟸5\text{items taken 4 at a time}\end{array}$$

  
  ::5C4*5物项一次取4件

  播放段落

  Next, set up the problem.
  ::下一个,设置问题。

  播放段落

  $$\begin{array}{r}{}_5{C}_4=\frac{5!}{4!(5-4)!}\end{array}$$

  
  ::5C4=5! 4! (5 - 4)! (5 - 4)!

  播放段落

  Then, fill in the numbers and simplify.
  ::然后,填满数字,简化。

  播放段落

  $$\begin{array}{r}{}_5{C}_4=\frac{(5)(4)(3)(2)(1)}{(4\cdot 3\cdot 2\cdot 1)(1)}=\frac{120}{24}=5\end{array}$$

  
  ::5C4=(5)(4)(3)(2)(1)(1)(1)(1)(4)(3)(2)(1)(1)(1)=12024=5

  播放段落

  The answer is there are 5 possible combinations.
  ::答案是,有5种可能的组合。

  播放段落

  Find the number of combinations in each example.
  ::在每个示例中查找组合数 。

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{array}{r}{}_5{C}_2\end{array}$
  ::5C2 5C2

  播放段落

  First, understand what  $\begin{array}{r}{}_5{C}_2\end{array}$  means.
  ::首先,了解5C2是什么意思。

  播放段落

  $$\begin{array}{r}{}_5{C}_2⟸5\text{items taken 2 at a time}\end{array}$$

  
  ::5C25物项一次取2件

  播放段落

  Next, set up the problem.

  $$\begin{array}{r}{}_5{C}_2=\frac{5!}{2!(5-2)!}\end{array}$$

  
  ::下一个,设置问题5C2=5! 2! (5-2)!

  播放段落

  Then, fill in the numbers and simplify.
  ::然后,填满数字,简化。

  播放段落

  $$\begin{array}{r}{}_5{C}_2=\frac{(5)(4)(3)(2)(1)}{(2\cdot 1)(3\cdot 2\cdot 1)}=\frac{120}{12}=10\end{array}$$

  
  ::5C2=(5)(4)(3)(2)(1)(21)(321)=12012=10

  播放段落

  The answer is there are 10 possible combinations.
  ::答案是,有10种可能的组合。

  播放段落

  Example 4
  ::例4

  播放段落

  $\begin{array}{r}{}_4{C}_3\end{array}$
  ::4C3 4C3

  播放段落

  First, understand what  $\begin{array}{r}{}_4{C}_3\end{array}$  means.
  ::首先,明白4C3的意思

  播放段落

  $$\begin{array}{r}{}_4{C}_3⟸4\text{items taken 3 at a time}\end{array}$$

  
  ::4C34物品一次取3件

  播放段落

  Next, set up the problem.

  $$\begin{array}{r}{}_4{C}_3=\frac{4!}{3!(4-3)!}\end{array}$$

  
  ::接下来,设置问题4C3=4! 3! (4- 3)!

  播放段落

  Then, fill in the numbers and simplify.
  ::然后,填满数字,简化。

  播放段落

  $$\begin{array}{r}{}_4{C}_3=\frac{(4)(3)(2)(1)}{(3\cdot 2\cdot 1)(1)}=\frac{24}{6}=4\end{array}$$

  
  ::4C3=(4)(3)(2)(1)(1)(1)(1)=246=4

  播放段落

  The answer is there are 4 possible combinations.
  ::答案是,有四种可能的组合。

  播放段落

  Example 5
  ::例5

  播放段落

  $\begin{array}{r}{}_6{C}_4\end{array}$
  ::6C4 6C4

  播放段落

  First, understand what  $\begin{array}{r}{}_6{C}_4\end{array}$  means.
  ::首先,明白6C4意味着什么。

  播放段落

   

  $$\begin{array}{r}{}_6{C}_4⟸6\text{items taken 4 at a time}\end{array}$$

  
  ::6C4*6物项一次取4件

  播放段落

  Next, set up the problem.
  ::下一个,设置问题。

  播放段落

  $$\begin{array}{r}{}_6{C}_4=\frac{6!}{4!(6-4)!}\end{array}$$

  
  ::6C4=6! 4! (6 -4)! (6 -4)!

  播放段落

  Then, fill in the numbers and simplify.
  ::然后,填满数字,简化。

  播放段落

  $$\begin{array}{r}{}_6{C}_4=\frac{(6)(5)(4)(3)(2)(1)}{(4\cdot 3\cdot 2\cdot 1)(2\cdot 1)}=\frac{720}{48}=15\end{array}$$

  
  ::6C4=(6)(5)(4)(3)(2)(1)(1)(4)(3)(2)(1)(4)(3)(2)(2)(2)(1)(4)(3)___________________(1)(2)(1)(2)(1)(2)(1)(2)(1)(2)(1)==72048=15

  播放段落

  The answer is there are 15 possible combinations.
  ::答案是,有15种可能的组合。

  播放段落

  Review
  ::回顾

  播放段落

  Evaluate each factorial.
  ::评估每个因素。

  1. 5!
  2. 4!
  3. 3!
  4. 8!
  5. 9!
  6. 6!

  播放段落

  Evaluate each combination using combination notation.
  ::使用组合符号对每种组合进行评价。

  播放段落
  7. $\begin{array}{r}{}_7{C}_2\end{array}$
     ::7C2 7C2
  播放段落
  8. $\begin{array}{r}{}_7{C}_6\end{array}$
     ::7C6 7C6
  播放段落
  9. $\begin{array}{r}{}_8{C}_4\end{array}$
     ::8C4 8C4
  播放段落
  10. $\begin{array}{r}{}_9{C}_6\end{array}$
      ::9C6
  播放段落
  11. $\begin{array}{r}{}_8{C}_3\end{array}$
      ::8C3 8C3
  播放段落
  12. $\begin{array}{r}{}_{10}{C}_7\end{array}$
      ::10C7 10C7
  播放段落
  13. $\begin{array}{r}{}_{12}{C}_9\end{array}$
      ::12C9 12C9
  播放段落
  14. $\begin{array}{r}{}_{11}{C}_9\end{array}$
      ::11C9 11C9
  播放段落
  15. $\begin{array}{r}{}_{16}{C}_{14}\end{array}$
      ::16C14 16C14

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。