2.3 解决平行线和三角线中缺失的角

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 解决平行线和三角形中缺失的角

  Collapse Expand

  解决平行线和三角形中缺失的角

  播放段落

  Building Bridges
  ::建筑桥梁

  播放段落

  Cables are used to help bridges support weight, but they do not prevent bridges from moving side to side. How can  a bridge be designed to prevent side-to-side movement?
  ::电缆被用来帮助桥梁的支撑重量,但并不妨碍桥梁的侧向移动。 如何设计桥梁来防止侧向移动?

  播放段落

  B ecause of their inherent strength, triangles are often used by engineers to add strength to a structure. In addition to housing, triangles are used in the design of roller coasters, stadiums, tables ,  and much more. In fact, any time you see any sort of construction that needs to support a lot of weight, you will likely see triangles.
  ::由于其内在力量,三角形常常被工程师用来增加结构的强度。除了住房外,三角形还被用于设计过山车、体育场、桌桌等等。 事实上,只要你看到任何需要支撑大量重量的建筑,你就会看到三角形。

  播放段落

  When engineers first began building suspension bridges to hold cars in the early 1900s, they focused on bridges that could support the proper weight, but they did not consider the effect of wind. Because of this,  bridges wobbled in extreme wind and some even collapsed. Take for instance the Tacoma Narrows Bridge. This bridge was built in 1938 without any triangular support structure. Due to this lack of strength, the bridge wobbled uncontrollably and eventually collapsed in 1940. When the bridge was rebuilt, it was nearly identical except for one feature: the triangular support structure lining the bottom of the bridge. The Tacoma Narrows Bridge is still standing strong today.
  ::19世纪初,工程师们开始建造悬架桥,以便扣留汽车。 当工程师们在19世纪初开始建造悬架桥时, 他们把注意力集中在能够支撑适当重量的桥梁上, 但是他们没有考虑风力的影响。 由于这个原因, 桥梁在极端风中摇摇欲坠, 有些甚至倒塌了。 例如塔科马纳罗斯桥。 这座桥建于1938年, 没有任何三角支持结构。 由于缺乏力量, 桥被摇摆不定, 最终在1940年坍塌了。 当桥梁重建时, 除了一个特征, 它几乎是一样的: 桥底的三角支持结构。 塔科马纳罗斯桥今天仍然坚固。

  

    

  ---

  播放段落

  Writ ing Angles With Expressions
  ::以表达式写入角度

  播放段落

  I n engineering, you  sometimes do  not know the exact dimensions you need, but do know the relationship between them. For example, the length of a rectangle might need to be twice as big as the width, or one angle might need to be ⅓ the measure of another angle. To  handle  this, engineers may  write multiple sides or angles in terms of one variable. This strategy is commonly used in computer software so that when one angle is determined, the rest can auto-populate without the need for calculation.
  ::在工程学中,有时你不知道你需要的准确尺寸,但确实知道它们之间的关系。例如,矩形的长度可能需要大于宽度的两倍,或者一个角度可能需要是另一个角度的1⁄3。要解决这个问题,工程师可以用一个变量写出多个边或角度。这个策略在计算机软件中常用,这样当一个角度被确定时,其余的可以自动传播,而不需要计算。

  播放段落

  Example
  ::示例示例示例示例

  播放段落
  • How could you express angle  $\begin{array}{r}a,\end{array}$  in the image below, terms of  $\begin{array}{r}x?\end{array}$
    ::您如何在下面的图像中表达 X 的角度 ?

  

  播放段落

  Since angle  $\begin{array}{r}a\end{array}$  is adjacent to the angle marked  $\begin{array}{r}\frac{1}{2}x\end{array}$  and the whole is specified as a right angle , you can say that the sum of angle  $\begin{array}{r}a\end{array}$  a nd   $\begin{array}{r}\frac{1}{2}x\end{array}$  is equal to 90 degrees.
  ::由于角a与标记为12x角的角相邻,而整个角被指定为右角,你可以说角a和角12x的和等于90度。

  播放段落

  First write this as an equation, then solve for  $\begin{array}{r}a:\end{array}$    
  ::先将此写成方程式, 然后解答 :

  播放段落

  $$\begin{array}{rl}a+\frac{1}{2}x& =90\\ a+\frac{1}{2}x-\frac{1}{2}x& =90-\frac{1}{2}x\\ a& =90-\frac{1}{2}x✓\end{array}$$

  
  ::a+12x=90a+12x-12x=90-12x=90-12x=90-12x__

  播放段落
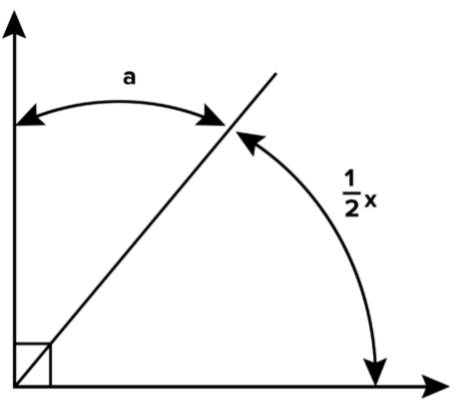
  • How c ould you express angle  $\begin{array}{r}a,\end{array}$  in the transversal below, in terms of  $\begin{array}{r}x?\end{array}$
    ::你如何用x表示一个角度, 在下面的横向角度?

  

  播放段落

  Since these are parallel lines crossed by a transversal, you know that the angle marked as  $\begin{array}{r}5x\end{array}$  is congruent to either of the two angles adjacent to angle  $\begin{array}{r}a.\end{array}$  On one side of $\begin{array}{r}a\end{array}$  is an alternate interior angle equal to  $\begin{array}{r}5x.\end{array}$  On the other side is an angle corresponding to  $\begin{array}{r}5x.\end{array}$  Since  $\begin{array}{r}\mathrm{\angle }a\end{array}$  is supplementary  to either of the adjacent angles (it forms a straight line either way), you can say that 180 degrees is equal to the measure of  $\begin{array}{r}a+5x:\end{array}$
  ::由于这些平行线是横跨横贯的, 您知道, 标为 5x 的角与角a 相邻的两个角中的任意一个吻合。 在一个一边是另一个内部角, 等于 5x 。 在另一边是 5x 的角。 由于 {a 是 任何一个相邻角的补充( 它构成一条直线) , 您可以说 180 度等于 +5x 的度量 :

  播放段落

  $$\begin{array}{rl}180& =a+5x\\ 180-5x& =a+5x-5x\\ 180-5x& =a✓\end{array}$$

  
  ::180=a+5x180 -5x=a+5x-5x=a+5x-5x-180-5x=a

   

  ---

  播放段落

  Ratios in Triangles
  ::三角间比率

  播放段落

  Another way to express angle and side length values is by using a ratio . When applied to triangles, ratios tell us that all the angles will be the result of multiplying each number in the ratio by the same scale factor .
  ::表达角值和边长值的另一种方式是使用比例。当应用到三角形时,比率告诉我们,所有角度都是将每个数字乘以同一比例系数的结果。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  T he  angles in a triangle  have the ratio 1:2:2. Find  the measure of each angle.
  ::三角形中的角度有1:2:2.2的比。 查找每个角度的度量。

  播放段落

  To get the angles, multiply the numbers in the ratio by the same factor , represented by  $\begin{array}{r}x.\end{array}$   E xpress the angles as  $\begin{array}{r}1x,2x,\text{ and }2x.\end{array}$   Additionally,  you know that the angles must add up to 180°. To find the value of the angles,  first write the information you have as  an equation:
  ::要获取角度,请将数字乘以相同系数,以 x 表示。将角度表示为 1x 2x 和 2x 。此外,您知道角必须加到 180 °。要找到角度的值,请先将您拥有的信息写成方程:

  播放段落

  $$\begin{array}{r}1x+2x+2x=180\end{array}$$

  
  ::1x+2x+2x=180

  播放段落

  Then c ombine like terms and simplify:
  ::然后,将诸如术语和简化的词句结合起来:

  播放段落

  $$\begin{array}{rl}5x& =180\\ x& =36\end{array}$$

  
  ::5x=180x=36

  播放段落

  By  substituting the value 36 in place of  $\begin{array}{r}x,\end{array}$  you  can find the measures of three angles:  $\begin{array}{r}1x=36,\end{array}$  and  $\begin{array}{r}2x=2(36)=72.\end{array}$
  ::通过替换值36来取代 x, 您可以找到三个角度的度量:1x=36, 2x=2( 36)=72。

  播放段落

  Use the interactive below to find the angles of a triangle with the ratio 2:3:4.
  ::使用下面的交互效果来找到一个三角形的角度,其比率为2:3:4。

   

  

  INTERACTIVE

  Triangle Ratios

  

  播放段落
  • Choose the correct angle measurements that correspond with the ratio 2:3:4.
    ::选择与比率2:3:4相对应的正确角度测量。
  播放段落
  • Click the button to check your answers.
    ::单击按钮检查您的答案 。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

   

  播放段落

  What are the ratios in an ? What are the ratios in a right isosceles triangle ? 
  ::正确的等分三角形中的比率是多少? 正确的等分三角形中的比率是多少?

   

  ---

  播放段落

  CK-12 PLIX Interactive: Bridge Design
  ::CK-12PLIX 互动:桥梁设计

  播放段落

  Explore angles, in architect plans for a bridge in the interactive below. The last of the 5 questions in the interactive is an open discussion question that can be answered in a forum.
  ::互动的5个问题中,最后的5个是公开讨论问题,可在论坛中回答。

   

   

  播放段落

   Summary
  ::摘要

  播放段落
  • Variables are useful  for representing  relationships between angles.
    ::变量可用于表示角度之间的关系。
  播放段落
  • T o find the measure of each angle given the ratio of angles in a triangle,  set up an equation   and use a variable to represent the scale factor.
    ::要根据三角形中角度比例来找到每个角度的度量, 设置方程, 并使用变量代表比例系数 。