6.11 辨别理论并将其应用到三角共性

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 辨识和将定理应用到三角共性

  Collapse Expand

  辨识和将定理应用到三角共性

  

  播放段落

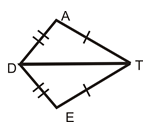
  Justin wants to make a , so he created the following pattern.
  ::贾斯汀想做一个, 所以他创造了以下模式。

  

  播放段落

  Justin needs to be sure that each triangle is congruent . He knows that there is a way to do this, but he can’t remember how to figure this out.
  ::贾斯汀需要确保每个三角形都是一致的。 他知道有办法做到这一点,但他不记得该如何解决。

  播放段落

  In this concept, you will learn to identify and apply theorems to test triangle congruence .
  ::在此概念中,您将学会识别和运用定理来测试三角一致性。

  播放段落

  Triangle Theorems
  ::三角三角定理

  播放段落

  If you can identify the congruent sides and angles of polygons then you can use this to determine congruence. If the corresponding sides and the of any two polygons are congruent, then you know that the two polygons are also congruent.
  ::如果您可以辨别多边形的一致边和角度, 那么您就可以用它来确定一致性。 如果对应边和任何两个多边形的一致, 那么您就会知道这两个多边形也是相同的。

  播放段落

  You can also work with triangles, because after all a triangle is also a polygon . Triangles are unique because there are a few rules that can be used to help identify whether or not two triangles are congruent. If you learn these rules, then you won’t have to compare every angle and every side to determine whether or not two triangles are congruent.
  ::您也可以使用三角形, 因为所有三角形后都是一个多边形。 三角形是独一无二的, 因为有一些规则可以用来帮助确定两个三角是否相容。 如果您学习了这些规则, 那么您就不必比较每个角度和每个侧面来确定两个三角形是否相容。

  播放段落

  The first rule represents the side-side-side, or , relationship. It says that if each side of one triangle is congruent to a corresponding side of a second triangle, then the two triangles are congruent. It is not necessary to check the angles. In a triangle the longest side is always opposite the largest angle. The shortest side is always opposite the smallest angle. If the corresponding sides of two triangles are congruent then the corresponding angles opposite these sides are also congruent.
  ::第一个规则代表侧侧侧或关系。 它表示, 如果一个三角形的每个侧面都与第二个三角形的对应侧对齐, 那么两个三角形是相同的。 没有必要检查角度。 在三角形中, 最长的侧面总是对着最大的角度。 最短的侧面总是对着最小的角度。 如果两个三角形的对应侧面是相同的, 那么对面的对角也是相同的 。

  播放段落

  The second rule says that if one angle and the sides adjacent to it in one triangle are congruent to an angle and its adjacent sides in the second triangle, the triangles will be congruent. You call this the side-angle-side (SAS) rule. In other words, if two sides of a triangle and the angle they make are congruent to two sides and the angle they make of a second triangle, then the triangles are congruent. Remember that the angle must be located between the two sides.
  ::第二条规则规定,如果一个三角形中一个角及其相邻的两边与一个角相匹配,第二个三角形中其相邻的两边相同,则三角形是相同的。您称此为侧角规则。换句话说,如果三角形的两边和角与两边和第二个三角形的角相匹配,则三角形是相同的。记住角必须位于两边之间。

  播放段落

  The third rule says that if two angles and the side between them in one triangle are congruent to two angles and the side between them in the second triangle, the two triangles are congruent. This is the angle-side-angle (ASA) rule. You can determine congruence just by knowing two angles and one side.
  ::第三条规则规定,如果一个三角形中两个角度和它们之间的侧面与两个角度一致,第二个三角形中两个角度和它们之间的侧面一致,这两个三角形是相同的。这是角度对角规则。通过了解两个角度和一边就可以确定一致性。

  播放段落

  Let’s look at an example.
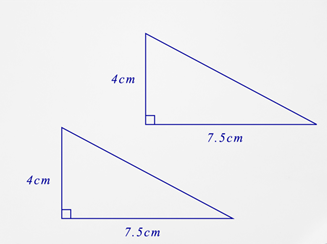
  ::让我们举个例子。

  播放段落

  Are the triangles below congruent? Explain your reasoning.
  ::三角形是否吻合?

  

  播放段落

  First, start by looking at the triangles and looking for the given information. Three side measurements must be known for SSS. A side measurement, an angle measure and a side measurement is necessary for . An angle measure, a side measurement and an angle measure must be known for ASA .
  ::首先,首先查看三角形并查找给定的信息。 SSS 必须知道三种侧边测量。 侧边测量、 角度测量和侧边测量是必需的 。 ASA 必须知道角测量、 侧测量和角测量 。

  播放段落

  For the above diagram , the sides which have a measurement of 4 cm are corresponding sides of the triangles. Likewise, the sides which have a measurement of 7.5 cm are also corresponding sides of the triangles. This is not information to call the triangles congruent.
  ::对于上图,测量量为4厘米的两边是三角形的对应边。同样,测量量为7.5厘米的两边也是三角形的对应边。这不是称三角形一致的信息。

  播放段落

  Next, decide which rule can be used to check for congruence? The SSS relationship cannot be used because only the lengths of two sides are known. The SAS relationship can be used. Remember, to use SAS, the angle must be between the two sides. In the first triangle, the angle between the two sides is a right angle which has a measure of 90°. The second triangle also has a right angle between the 7.5 and 4 centimeter sides. Using the SAS rule, the triangles can be compared: 7.5 centimeters (side), 90° (angle), 4 centimeters (side).
  ::下一步, 决定哪个规则可以用于检查一致性 ? SSS 关系无法使用, 因为只知道两边的长度 。 SAS 关系可以使用 SS 关系 。 记住, 要使用 SAS , 角度必须是两边。 在第一个三角中, 两边的角是右角, 角度为90°。 第二个三角在 7.5 和 4 厘米两边也有右角 。 使用 SAS 规则, 三角可以比较: 7.5 厘米( 侧) 、 90°( 角) 、 4 厘米( 侧) 。

  播放段落

  The answer is the triangles are congruent by applying the SAS rule.
  ::答案是,三角形通过应用SAS规则是一致的。

  播放段落

  Let’s look at another example.
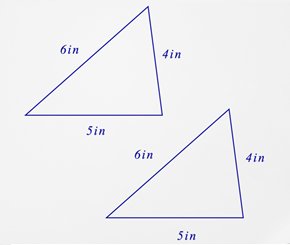
  ::让我们再看看另一个例子。

  播放段落

  Are these two triangles congruent? Explain your reasoning.
  ::这两个三角形是否吻合?

  

  播放段落

  First, start by looking at the triangles and looking for the given information. Three side measurements must be known for SSS. A side measurement, an angle measure and a side measurement is necessary for SAS. An angle measure, a side measurement and an angle measure must be known for ASA.
  ::首先,首先查看三角形并查找给定的信息。 SSS 必须知道三个侧边测量。 SAS 需要一个侧边测量、一个角度测量和一个侧边测量。 ASA 必须知道一个角度测量、一个侧边测量和一个角度测量。

  播放段落

  Next, decide which rule can you use to check for congruence? No measures are given for any of the angles in either triangle so neither the SAS nor the ASA rule can be used to show congruence. However, the measurements of the sides are given. The SSS rule can be used to compare the triangles to determine congruence. Remember the sides that are equal in length must be corresponding sides of the triangles. In the first triangle, the side lengths are 4 in (side), 5 in (side), and 6 in (side). These are the same measurements of the corresponding sides of the second triangle.
  ::下一步, 决定您可以使用哪一条规则来检查是否一致? 没有给三角形中的任何角设定任何措施, 所以 SAS 和 ASA 规则都无法用来显示一致性。 但是, 给出了两边的测量结果 。 SSS 规则可以用来比较三角形, 以确定一致性 。 记住长度相等的两边必须是三角形的对应边。 在第一个三角形中, 侧长是 4 个( 侧边 ) 、 5 个( 侧) 和 6 个( 侧边 ) 。 这些是第二个三角形相应边的相同的测量结果 。

  播放段落

  The answer is the triangles are congruent because of the SSS rule.
  ::答案是三角形与SSS规则一致。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about  the pattern that Justin drew for his kite.
  ::早些时候,有人给了你一个问题 关于贾斯汀为他的风筝画的图案

  

  播放段落

  First, let’s think about which theorem he can use to prove that the two triangles are congruent. These triangles share a common side $\begin{align*}(\overline{DT})\end{align*}$ , this side is congruent in both triangles. The same tic marks show that the other two sides are congruent as well.
  ::首先,让我们想想他可以用什么理论来证明这两个三角是相同的。 这两个三角有着共同的一面(DT ) , 这边是两个三角的一面。 同样的语气标记也表明其他两面也是相同的。

  播放段落

  Next, since three sides of one triangle are congruent to three corresponding sides of the other triangle, then the triangles are congruent using the SSS Rule.
  ::其次,由于一个三角形的三边与另一个三角形的三对对应两对齐,因此三角形使用SSS规则是相同的。

  播放段落

  The answer is the triangles are congruent using the SSS Rule.
  ::答案是三角形使用 SSS 规则是一致的 。

  播放段落

  Justin has been successful in proving congruency.
  ::贾斯汀成功地证明是一致的。

  播放段落

  Example 2
  ::例2

  播放段落

  Use this illustration to answer the following question.
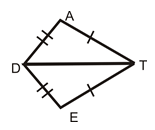
  ::使用此插图回答下列问题。

  播放段落

  

  
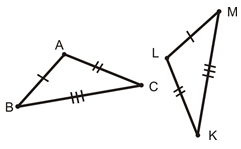
  Which theorem could you use to prove that these triangles are congruent? Explain your thinking.
  ::你用什么理论来证明这些三角形是相同的?

  播放段落

  First, notice that no angle measures or side measurements have been given. However, same tic marks indicate same side lengths. Each side of triangle $\begin{align*}ABC \end{align*}$  has a corresponding side length of the same measure in triangle $\begin{align*}LKM\end{align*}$ .
  ::首先,请注意没有给出角度量或侧边测量。 但是, 相同的微分标记表示相同的侧长。 三角形ABC 的每侧在三角形 LKM 中都有相应的边长。

  播放段落

  The answer is the triangles are congruent because of the SSS rule.
  ::答案是三角形与SSS规则一致。

  播放段落

  Name the theorem that you could use to prove triangle congruence based on each description.
  ::根据每个描述来证明三角形的一致性,请列出您可用以证明该三角形一致性的定理。

  播放段落

  Example 3
  ::例3

  播放段落

  You have been given two side lengths and the included angle measure in each of two triangles.
  ::在两个三角形的每个三角形中,给您设定了两个侧边长度和包含的角度度量。

  播放段落

  The answer is ASA.
  ::答案是ASA。

  播放段落

  Example 4
  ::例4

  播放段落

  You have been given two angle measures and one side length in each of two triangles
  ::在两个三角形的每个三角形中,给您两个角度度量和一边长度

  播放段落

  The answer is SAS.
  ::答案是SAS。

  播放段落

  Example 5
  ::例5

  播放段落

  You have been given three side lengths and no angle measures in each of two triangles.
  ::在两个三角形中,每个三角形都有三个侧边长度,没有角度量。

  播放段落

  The answer is SSS.
  ::答案是SSS。

  播放段落

  Review
  ::回顾

  播放段落

  Use the given information to figure out each congruence statement.
  ::使用给定的信息来计算每一份一致的语句。

  播放段落

  $\begin{align*}\triangle ABC \cong \triangle DEF\end{align*}$
  ::ABC*DEF ABC*DEF ABC* ABC*DEF ABC* ABC*DEF ABC* ABC* ABC*DEF ABC* ABC* ABC*DEF ABC * ABC* ABC* ABC*DEF * ABC* ABC*DEF ABC * ABC* ABC * ABC*DEDEF * ABC* ABC * ABC* ABC* ABC*DEF (ABC * ABC* ABC * ABC* ABC DEDEF (ABC AB(ABC ) (ABC ABC ABC*DE DE, ABC(ABC ABC DEF, AB(ABC ABC) (ABC ABD AB(ABD) (ABC) (ABC AB(ABC) (ABC) (AB(ABC) (AB) (ABC) (ABC) (ABC) (AB(ABC) (ABC) (AB) (ABC) (ABC) (AB) (AB) (ABC) (ABC) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB) (AB)

  播放段落

  1.  $\begin{align*}\angle A \cong \underline{\;\;\;\;\;\;\;\;}\end{align*}$
  ::1. A

  播放段落

  2.  $\begin{align*}\angle B \cong \underline{\;\;\;\;\;\;\;\;}\end{align*}$
  ::2. B____________________________________________________________________________________________________________________________________

  播放段落

  3.  $\begin{align*}\angle C \cong \underline{\;\;\;\;\;\;\;\;}\end{align*}$
  ::3 CCCCCCCCCCCCCCCC

  播放段落

  4.  $\begin{align*}\overline{AB} \cong \underline{\;\;\;\;\;\;\;\;}\end{align*}$
  ::4. AB _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  5.  $\begin{align*}\overline{BC} \cong \underline{\;\;\;\;\;\;\;\;}\end{align*}$
  ::5. BC ____________________________________________________________________________________________________________________________________________________________________________

  播放段落

  6.  $\begin{align*}\overline{AC} \cong \underline{\;\;\;\;\;\;\;\;}\end{align*}$
  ::6.C AC __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  7. If line segment $\begin{align*}AC\end{align*}$  has a length of 8, which other segment also has a length of 8?
  ::7. 如果 " AC " 分支部分的长度为8, 则其他哪些部分的长度也为8?

  播放段落

  8. If angle $\begin{align*}A\end{align*}$  has a measure of 55°, which other angle has a measure of 55°?
  ::8. 如果角度A的测量度为55°,其他哪个角度的测量度为55°?

  播放段落

  9. If angle $\begin{align*}B\end{align*}$  has a measure of 45°, which other angle has a measure congruent to that?
  ::9. 如果角度B的测量度为45°,那么哪个其他角度的测量度与该值一致?

  播放段落

  10. If these two triangles are congruent, are the side lengths and angle measures the same?
  ::10. 如果这两个三角形是相同的,侧边长度和角测量的长度是否相同?

  播放段落

  11. Would these two triangles look identical?
  ::11. 这两个三角形看起来一样吗?

  播放段落

  Name the theorem that would best prove triangle congruence based on each description.
  ::根据每个描述, 命名最能证明三角一致的定理 。

  播放段落

  12. Three side lengths, 6 inches, 5 inches and 4 inches.
  ::12. 三个侧长,6英寸,5英寸和4英寸。

  播放段落

  13. One angle measure and two side lengths.
  ::13. 一个角度尺度和两个边长。

  播放段落

  14. Two angle measures and one side length.
  ::14. 两种角度衡量尺度和一面长度。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。