课程： 7.1 评价激进表达式

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节评价激进言论

折叠展开
评价激进言论
Mark, a huge baseball fan, asked his sister Sara, “Did you know that the distance between any two bases on a baseball diamond is equal to the square root of 8100?”
::一个巨大的棒球球迷Mark问他的妹妹Sara:“你知道棒球钻石上两个基地之间的距离等于8100平方根吗?”

How can Sara learn or estimate the square root of 8100?
::Sara如何学会或估计8100的平方根?

In this concept, you will learn to evaluate radical expressions.
::在这个概念中,你将学会评价激进的表达方式。

Radical Expressions
::激进言论

An exponent is the small number to the upper right of a base that tells you how many times to multiply the base times itself. For example $\begin{align*}7^2 = 7 \times 7 = 49\end{align*}$ . The base of 7 is raised to the power of 2 which means to multiply 7 times itself twice. The answer is 49.
::引号是基底右上方的小数字,该数字可以告诉你乘基数本身多少倍。例如,72=7×7=49。7的基数提高到2的功率,这意味着乘以7倍本身。答案是49。

Finding the square root of a number is the inverse operation of squaring. The square root of a number ‘ $\begin{align*}n\end{align*}$ ,’ denoted by $\begin{align*}\sqrt{n}\end{align*}$ , is a positive number whose square is $\begin{align*}n\end{align*}$ . The $\begin{align*}\sqrt{n}\end{align*}$ is called a radical. A radical is an expression consisting of a radical sign $\begin{align*}\sqrt{}\end{align*}$ , a radicand which is the number or term under the radical sign and an index which is the small number outside the radical sign which indicates what root to find. The index for ‘square root’ is two but it is never written in the expression - it is understood since the radical sign with no index is referred to as the square root.
::查找数字的平方根是正方根的反作用。 n 表示的数字 'n ' 的正方根是一个正数,正方数为n。 n 称为激进。激进是一个由激进符号组成的表达式,即激进符号下的数字或术语,而指数是激进符号外的少量数字,表示要找到什么根。`正方根 ' 的索引是两个,但从未写在表达式中,因为没有指数的激进符号被称为正方根,所以人们理解这一点。

The following is an example of a radical.
::以下是激进的一个例子。

$\begin{aligned} \begin{array}{rcl} ↓ radical sign \\ index \to \sqrt[3]{64} \leftarrow radicand \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} && \qquad \ \ \ \ \ \downarrow \text{radical sign}\\ && {\color{red}\text{index} \rightarrow} \sqrt[{\color{red}3}]{{\color{blue}64}} {\color{blue}\leftarrow \text{radicand}} \end{array}\end{align*}$
::雷达标志 index_643radicand

When a number is written under a radical sign, you are finding the square root of that number. For the radical $\begin{align*}\sqrt{49}\end{align*}$ you are finding the number times itself twice that equals 49. The answer is 7. Forty-nine is called a perfect square because it is a number that can be written as a power with an integer base and the exponent 2.
::当一个数字在一个激进符号下写下时,您正在找到该数字的平方根。对于激进49,您正在发现数字本身的两倍等于49的两倍。答案是7。49被称为完美方块,因为它是一个数字,可以用整数基和指数2来写成。

A number raised to the power of 3 is said to be cubed . For example $\begin{align*} 4^3 = 4 \times 4 \times 4 = 64\end{align*}$ . The base of 4 has been multiplied by itself three times. The inverse operation would involve finding the cube root of 64
::向 3 功率 3 的数调的数据说是立方体。例如, 43=4x4x4x4=64。基数 4 的基数本身乘了三次。反向操作需要找到 64 的立方根。

The cube root of 64 is the number times itself three times that equals 64. The expression can be written as $\begin{align*} \sqrt[3]{64} =3\end{align*}$ . Sixty-four is called a perfect cube because it is a number that can be written as a power with an integer base and the exponent 3.
::64 的立方根是等于64的三倍数乘以本身的乘数。表达式可以写为 643=3。 64 被称为完美立方体, 因为它是一个数字, 可以写成具有整数基和指数3的功率。

Not all numbers are perfect squares or perfect cubes. The values for these numbers can either be estimated or found using the TI calculator. If you were asked to find the square root of thirty then you could estimate the answer.
::并非所有数字都是完美的方块或完美的立方体。这些数值的值要么可以估计,要么可以使用TI计算器找到。如果要求您找到30的平方根,那么您可以估计答案。

$\begin{align*}\sqrt{30}\end{align*}$ is between the two perfect squares $\begin{align*} 25 = 5^2 \text{ and } 36 = 6 ^ 2\end{align*}$ . Since 30 is approximately half-way between 25 and 36, then an estimate of 5.5 would be a reasonable answer for the square root of 30.
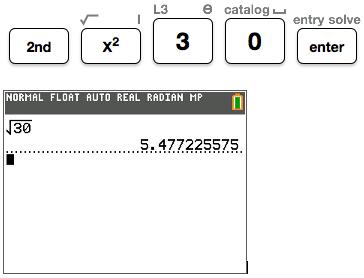
::30是两个完美的平方之间25=52和36=62。由于30大约在25至36之间中间,因此,估计的5.5将是30平方根的合理答案。

You could also determine the value of $\begin{align*}\sqrt{30}\end{align*}$ using the TI calculator.
::您也可以使用 TI 计算器确定 30 的值。

Using the TI calculator press the keys in the order shown below.
::使用 TI 计算器按以下顺序按键。

The estimate of 5.5 is the same as the calculator answer if it were rounded to the nearest tenth.
::如果四舍五入至最近的十分之一,5.5的估计数与计算答案相同。

Estimate the following:
::估计如下:

$\begin{align*}\sqrt[3]{35}\end{align*}$

Thirty-five is not a perfect cube since there is no integer when multiplied by itself 3 times equal to 35.
::355不是完美的立方体,因为当3乘以等于35的3倍时,没有整数。

The value 35 is between the perfect cube $\begin{align*}27= 3 \times 3 \times 3 = 3 ^3 \end{align*}$ and $\begin{align*}64= 4 \times 4 \times 4 = 4 ^ 3\end{align*}$ . The number 35 is closer to 27 than it is to 64. Therefore an estimate for the cube root of 35 is 3.3.
::值 35 是在 27= 3x3x33=33 和 64= 4x4x4=43 的完美立方体 27 = 3x3x3=33 和 64= 4x4x4=43 之间。数字 35 比 64 接近 27 。因此, 立方根为 35 的估计数是 3. 3 。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Mark and the baseball diamond. His sister wants to figure out the square root of 8100.
::早些时候,你被问及马克和棒球钻石的问题。他姐姐想找出8100的平方根。

First, rewrite the square root of 8100 as a radical.
::首先,将8100的平方根改写为激进分子。

$\begin{aligned} \sqrt{8100} \end{aligned}$
$\begin{align*}\sqrt{8100}\end{align*}$

Next, write the square root of 8100 as $\begin{align*}\sqrt{81} \times \sqrt{100} \end{align*}$
::下一步, 将 8100 的平方根写为 81x100 。

Next, write the square of 81.
::下一个,写出81的方形

$\begin{aligned} 81 = 9 \times 9 = 9^{2} \end{aligned}$
$\begin{align*}81= 9 \times 9 = 9^2 \end{align*}$ The square of 81 is 9.
::81=9x9=92 81平方为9。

Next, write the square of 100.
::下一个,写上100平方

$\begin{aligned} 100 = 10 \times 10 = 10^{2} \end{aligned}$
$\begin{align*}100 = 10 \times 10 = 10^2\end{align*}$ The square of 100 is 10.
::100=10x10=102 100平方是10

Then, multiply the two squares.
::然后,乘以两个方形。

$\begin{aligned} 9 \times 10 = 90 \end{aligned}$
$\begin{align*}9 \times 10 = 90\end{align*}$

The answer is 90.
::答案是90

The distance between any two bases is 90 feet.
::任何两个基地之间的距离是90英尺。

Example 2
::例2

Estimate the square root of the following by listing the two squares that the root falls between:
::通过列出根在以下两端之间的两个方块来估计以下方块的平方根:

$\begin{aligned} \sqrt{74} \end{aligned}$
$\begin{align*}\sqrt{74}\end{align*}$

First, figure out the perfect square that is closest to but less than 74.
::首先,找出最接近但少于74的完美方形。

$\begin{aligned} 64 = 8^{2} \end{aligned}$
$\begin{align*}64 = 8 ^2\end{align*}$

Next, figure out the perfect square that is closest to but greater than 74.
::接下来,找出最接近但大于74的完美方形。

$\begin{aligned} 81 = 9^{2} \end{aligned}$
$\begin{align*}81 = 9^2\end{align*}$

The answer is 8 and 9.
::答案是8和9

$\begin{align*}\sqrt{74}\end{align*}$ is between 8 and 9.
::74在8到9之间。

Example 3
::例3

Using the TI calculator, calculate the following square root to the nearest hundredth.
::使用 TI 计算器计算以下的平方根到最近的一百个。

$\begin{aligned} \sqrt{115} \end{aligned}$
$\begin{align*}\sqrt{115}\end{align*}$

First, press the buttons $\begin{align*} 2 ^{nd} \ x^2 \end{align*}$ 1 1 5 enter
::首先,按下按钮 2nd x2 1115 输入

Next, look at the answer displayed on the screen of the calculator.
::接下来,看看计算器屏幕上显示的答案。

$\begin{aligned} 10.72380529 \end{aligned}$
$\begin{align*}10.72380529\end{align*}$

Then, round the answer to two places after the decimal point .
::然后,在小数点后,将答案绕到两个地方。

$\begin{aligned} 10.73 \end{aligned}$
$\begin{align*}10.73\end{align*}$

The answer is $\begin{align*} \sqrt{115} \approx 10.73\end{align*}$
::答案是11510.73

Example 4
::例4

Without using technology, which of the following numbers are perfect squares? Justify your answer.
::不使用技术,以下数字中哪一个是完美的方形?请说明答案的理由。

$\begin{aligned} 196 120 36 \end{aligned}$
$\begin{align*}196 \ \ \ 120 \ \ \ 36\end{align*}$

Create a factor tree for each of the given numbers.
::为每个给定数字创建因子树。

First, 196 is an even number so divide it by two.
::首先,196是偶数,所以除以2。

$\begin{aligned} \frac{196}{2} = 98 \end{aligned}$
$\begin{align*}\frac{196}{2} = 98 \end{align*}$

Next, 98 is an even number so divide it by two.
::接下来,98是偶数,再除以2。

$\begin{aligned} \frac{98}{2} = 49 \end{aligned}$
$\begin{align*}\frac{98}{2} = 49 \end{align*}$

Next, write down the numbers that will multiply to give 49.
::下一位,写下49个数字的乘数。

$\begin{aligned} 7 \times 7 \end{aligned}$
$\begin{align*}7 \times 7\end{align*}$

Next, list all the factors used to simplify 196.
::下面列出用于简化196条的所有因素。

$\begin{aligned} 2, 2, 7, 7 \end{aligned}$
$\begin{align*}2,2,7,7\end{align*}$

Next, make two groups of same factors.
::其次,将同样的因素分为两组。

$\begin{aligned} 2 \times 7 and 2 \times 7 \end{aligned}$
$\begin{align*}2 \times 7 \text{ and }2 \times 7\end{align*}$
::2×7和2×7

Then, multiply each group of factors.
::然后,乘以每一组因素。

$\begin{aligned} 14 and 14 \end{aligned}$
$\begin{align*}14 \ \text{and} \ 14\end{align*}$
The answer is 14.

$\begin{aligned} \sqrt{196} = 14 \end{aligned}$
$\begin{align*} \sqrt{196} = 14\end{align*}$

First, 120 is an even number so divide it by two.
::首先,120是偶数,因此除以2。

$\begin{aligned} \frac{120}{2} = 60 \end{aligned}$
$\begin{align*}\frac{120}{2} = 60\end{align*}$

Next, 60 is an even number so divide it by two.
::接下来,60是偶数,再除以2。

$\begin{aligned} \frac{60}{2} = 30 \end{aligned}$
$\begin{align*}\frac{60}{2} = 30\end{align*}$

Next, 30 is an even number so divide it by two.
::接下来 30是偶数所以除以2

$\begin{aligned} \frac{30}{2} = 15 \end{aligned}$
$\begin{align*}\frac{30}{2} = 15\end{align*}$

Next, write down the numbers that multiply to give 15.
::接下来,写下乘以15的数字

$\begin{aligned} 3 \times 5 \end{aligned}$
$\begin{align*}3 \times 5\end{align*}$

Next, list all the factors used to simplify 120.
::下面列出用于简化120的所有因素。

$\begin{aligned} 2, 2, 2, 3, 5 \end{aligned}$
$\begin{align*}2, 2, 2, 3, 5\end{align*}$

Then, make two groups of same factors.
::然后,将两个因素分为两组。

There are three 2’s, one 3, and one 5. Two groups of same factors cannot be made from these numbers.
::有三组,二组,一组,三组,五组。这些数字不能产生两组相同的因素。

120 is not a perfect square.
::120不是一个完美的正方形。

First, 36 is an even number so divide it by two.
::首先,36是偶数,因此除以2。

$\begin{aligned} \frac{36}{2} = 18 \end{aligned}$
$\begin{align*}\frac{36}{2} = 18\end{align*}$

Next, 18 is an even number so divide it by two.
::接下来,18是偶数,所以除以2。

$\begin{aligned} \frac{18}{2} = 9 \end{aligned}$
$\begin{align*}\frac{18}{2} = 9\end{align*}$

Next, write down the numbers that multiply to give 9.
::下一个,写下乘以 9 的数字。

$\begin{aligned} 3 \times 3 \end{aligned}$
$\begin{align*}3 \times 3\end{align*}$

Next, list all the factors used to simplify 36.
::下面列出用于简化36的所有因素。

$\begin{aligned} 2, 2, 3, 3 \end{aligned}$
$\begin{align*}2, 2, 3, 3\end{align*}$

Next, make two groups of same factors.
::其次,将同样的因素分为两组。

$\begin{aligned} 2 \times 3 and 2 \times 3 \end{aligned}$
$\begin{align*}2 \times 3 \text{ and } 2 \times 3\end{align*}$
::2×3和2×3

Then, multiply each group of factors.
::然后,乘以每一组因素。

$\begin{aligned} 6 and 6 \end{aligned}$
$\begin{align*}6 \ \text{and} \ 6\end{align*}$
::第六条和第六条

The answer is 6.
::答案是6个

$\begin{aligned} \sqrt{36} = 6 \end{aligned}$
$\begin{align*}\sqrt{36} = 6\end{align*}$

Review
::回顾

Evaluate each radical expression without using technology.
::在不使用技术的情况下评价每个激进的表达方式。

1. $\begin{align*}\sqrt{16}\end{align*}$

2. $\begin{align*}\sqrt{25}\end{align*}$

3. $\begin{align*}\sqrt{81}\end{align*}$

4. $\begin{align*}\sqrt{121}\end{align*}$

5. $\begin{align*}\sqrt{36}\end{align*}$

6. $\begin{align*}\sqrt{169}\end{align*}$

7. $\begin{align*}\sqrt[3]{125}\end{align*}$

8. $\begin{align*}\sqrt[3]{64}\end{align*}$

9. $\begin{align*}\sqrt[3]{27}\end{align*}$

10. $\begin{align*}\sqrt{144}\end{align*}$

Approximate each square root by listing the two values that the square root can be found between.
::通过列出平方根在中间可以找到的两个值, 接近每个平方根。

11. $\begin{align*}\sqrt{12}\end{align*}$

12. $\begin{align*} \sqrt{15}\end{align*}$

13. $\begin{align*}\sqrt{20}\end{align*}$

14. $\begin{align*} \sqrt{22}\end{align*}$

15. $\begin{align*}\sqrt{31}\end{align*}$

16. $\begin{align*}\sqrt{90}\end{align*}$

17. $\begin{align*} \sqrt{99}\end{align*}$

Review (Answers)
::回顾(答复)
Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.

章节大纲

常规

评价激进言论

Radical Expressions ::激进言论

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Radical Expressions
::激进言论

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)