Course: 7.6 衍生和使用毕达哥里定理

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

提取并使用毕达哥里定理

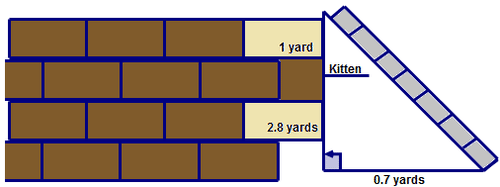
lesson content

Tracy’s kitten is stuck 2.8 yards above the ground on the window sill of her Grandma’s house. Her grandma is not at home so she decides to rescue her terrified kitten with help from her friends. For safety reasons, the base of the ladder must be 0.7 yards away from the house and extend 1 yard above the window sill. The ladder she has borrowed is 4 yards in length.
::Tracy的小猫被困在外婆家的窗户旁的地上2.8码处。她奶奶不在家,因此她决定在朋友的帮助下救救她吓坏了的小猫。出于安全原因,梯子的底部必须离房子0.7码,宽到窗子上方1码。她借来的梯子长4码。

As Tracy positions the ladder in place, she looks up and wonders if the ladder is going to be tall enough for her to rescue her kitten.
::当Tracy把梯子放在位置上时, 她抬起头来想知道梯子是否足够高, 足以让她救回小猫。

In this concept, you will learn to derive and use the Pythagorean Theorem .
::在这个概念中,你将学会获取和使用毕达哥伦神话。

Pythagorean Theorem
::毕达哥里安神论

Triangles are often named according to the measure of the angles they contain. An acute triangle has three angles such that each of the three angles is less than 90°. An obtuse triangle has two angles such that the measure of each of these angles is less than 90° and the measure of the third angle is greater than 90°. A right triangle has one angle that has a measure of 90° and two acute angles such that the sum of their measures equals 90°. The two acute angles of a right triangle are complementary – their sum equals 90°.
::三角形通常根据所包含角的测量量命名。尖三角形有三个角, 即三个角的每个角小于90°。尖三角形有两个角, 即每个角的测量量小于90°, 第三个角的测量量大于90°。右三角形有一个角, 其测量量为90°, 两个角的急性角, 其测量量总和等于90°。右三角形的两个急性角是互补的, 其总和等于90° 。

Of the three triangles shown in the above diagram , the right triangle is the one that is used most often in solving real world problems. This type of triangle has characteristics that are unique only to right triangles. Every triangle has three sides and three angles. The sides of a right triangle have names that apply only to a right triangle.
::在上述图表中显示的三个三角中,右三角是用来解决真实世界问题的最常见的三角。这种三角具有仅对右三角独有的特性。每个三角都有三个边和三个角度。右三角的两边有仅适用于右三角的名称。

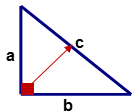
The two sides of the right triangle labeled ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ ’ are called the legs of the triangle. The side of the triangle opposite the right angle (90°) labeled ‘ $\begin{aligned} c \end{aligned}$ ’ is called the hypotenuse and it is the longest side of the right triangle. The names of the legs ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ ’ can be switched from one leg to the other but the hypotenuse ‘ $\begin{aligned} c \end{aligned}$ ’ must be the side opposite the right angle of the triangle.
::右三角的两侧标有 " a " 和 " b " ,称为三角的腿。右角(90°)标有 " c " 的三角的两侧称为 " potenuse " ,是右三角最长的一面。双腿 " a " 和 " b " 的名称可以从一条腿转到另一条腿,但下角 " c " 必须是三角右角对面的一面。

The relationship between the hypotenuse and the legs of a right triangle is defined by the which states that the square of the length of the hypotenuse is equal to the sum of the length of leg ‘ $\begin{aligned} a \end{aligned}$ ’ squared and the length of leg ‘ $\begin{aligned} b \end{aligned}$ ’ squared. The Pythagorean Theorem is stated by the equation.
::下限与右三角形腿的关系由以下条件界定:下限长度的正方形等于`a ' 平方腿长度和`b ' 平方腿长度的和。方程式说明了Pythagorian Theorem。

\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}

::c2=a2+b2 (千兆赫)

The equation representing the Pythagorean Theorem contains three pieces which are $\begin{aligned} a, b \end{aligned}$ and $\begin{aligned} c \end{aligned}$ . If you know two of these pieces, then the equation can be used to calculate the third piece. The Pythagorean Theorem can also be used to determine if a given triangle is indeed a right triangle.
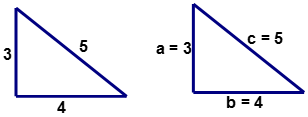
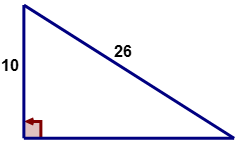
::代表 Pytagorean 定理的方程式包含三块, 其中三块是 a, b 和 c。如果您知道其中两块, 那么该方程式可以用来计算第三块。 Pytagorean 定理也可以用来确定给定三角形是否是一个右三角形。

Look at the triangle given below. There is no right angle marked to indicate that the triangle is a right triangle. Is the triangle a right triangle? The Pythagorean Theorem can be used to answer this question.
::查看下面给定的三角形。没有右角标记显示三角形是右三角形。三角形是右三角形吗? Pytagoren Theorem 可以用来回答这个问题。

\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}

::c2=a2+b2 (千兆赫)

First, fill in the values for the letters $\begin{aligned} a, b \end{aligned}$ and $\begin{aligned} c \end{aligned}$ .
::首先,填写字母a、b和c的值。

\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (5)^{2} & = & (3)^{2} + (4)^{2} \end{array} \end{aligned}

::c2=a2+b2(5)2=(3)2+(4)2

Next, perform the indicated operations on both sides of the equation.
::接下来,在等式的两侧执行指示的行动。

\begin{aligned} \begin{array}{rcl} (5)^{2} & = & (3)^{2} + (4)^{2} \\ (5 \times 5) & = & (3 \times 3) + (4 \times 4) \\ 25 & = & 9 + 16 \end{array} \end{aligned}

Then, simplify the equation by adding the values on the right side of the equation.
::然后,简化方程式,在方程式右侧添加值。

\begin{aligned} \begin{array}{rcl} 25 & = & 9 + 16 \\ 25 & = & 25 \end{array} \end{aligned}

Both sides of the equation are equal. The values of (3, 4, and 5) resulted in $\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}$ being a true statement of equality. Therefore, the given triangle is a right triangle.
::等式的两面是相等的。数值( 3、 4和 5) 导致 c2=a2+b2 是一个真正的平等声明。因此, 给定的三角形是一个右三角形。

The values of (3, 4, and 5) for the positive integers $\begin{aligned} (a, b, c) \end{aligned}$ respectively, is a combination of numbers known as a Pythagorean Triple which are a set of three whole numbers that satisfy the Pythagorean Theorem $\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}$ . Other can be generated by multiplying the values of any known Pythagorean Triple by any positive integer. If the values (3, 4, and 5) are multiplied by 2 then another Pythagorean Triple (6, 8, and 10) is created. If the values (6, 8, and 10) are multiplied by 4 then another Pythagorean Triple (24, 32, and 40) is generated.
::正数整数(a,b,c)的数值(3,4和5)分别是称为Pythagorean Triple的数值组合(3,4和5),它们是一组三整数,满足Pythagoren Theorem c2=a2+b2.其他数值可以通过将已知的Pytagoren Triple的数值乘以正数整数而生成。如果数值(3,4和5)乘以2乘以2,再创建一个Pythagoren Triple(6,8和10),如果数值乘以4(6,8和10),再产生另一个Pythagoren Triple(24,32和40)。

The newly generated values have been substituted into the Pythagorean Theorem, $\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}$ , to ensure that they are Pythagorean Triples.
::新生成的数值已被替换为Pytagorean Theorem, c2=a2+b2,以确保它们是Pytagorean Triples。

\begin{aligned} \begin{array}{rcl} c^{2} = a^{2} + b^{2} c^{2} = a^{2} + b^{2} \\ (10)^{2} = (6)^{2} + (8)^{2} (40)^{2} = (24)^{2} + (32)^{2} \\ (10 \times 10) = (6 \times 6) + (8 \times 8) (40 \times 40) = (24 \times 24) + (32 \times 32) \\ 100 = 36 + 64 1600 = 576 + 1024 \\ 100 = 100 1600 = 1600 \end{array} \end{aligned}

::c2=a2+b2 c2=a2+b2 c2=a2+b2(102)2=(6)2+(8)2(402=(242)+(322(10x10)=(6x6)+(8x8)+(8x40)=(24x24)+(32x3232)100=36+641600=576+1024100=1001600=1600

Each of the new Pythagorean Triples have resulted in $\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}$ being a true statement of equality.
::每一个新的《毕达哥伦三宝》都使C2=a2+b2成为真正的平等声明。

If you know that a given triangle is a right triangle, then the Pythagorean Theorem can be used to calculate the length of an unknown side of the triangle when you know the lengths of two of the sides.
::如果您知道给定的三角形是右三角形,那么当您知道两边的长度时, Pytagorean 理论可以用来计算三角形未知侧的长度。

Let’s look at an example.
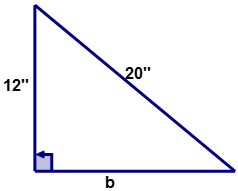
::让我们举个例子。

For the following right triangle, calculate the length of the unknown side ‘ $\begin{aligned} b \end{aligned}$ ?’
::对于以下的右三角形,计算未知边“b”的长度。

First, use the Pythagorean Theorem to calculate the length of side ‘

\begin{aligned} b \end{aligned}

.’
::首先,使用毕达哥里安神话来计算“b”边的长度。

\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}

::c2=a2+b2 (千兆赫)

Next, fill in the values given for sides ‘ $\begin{aligned} a \end{aligned}$ ’ and side ‘ $\begin{aligned} c \end{aligned}$ .’
::接下来,填充给“a”和“c”两边的数值。

\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (20)^{2} & = & (12)^{2} + b^{2} \end{array} \end{aligned}

::c2=a2+b2(202)=(12)2+b2

Next, perform the indicated operations.
::下一步,执行所述行动。

\begin{aligned} \begin{array}{rcl} (20)^{2} & = & (12)^{2} + b^{2} \\ (20 \times 20) & = & (12 \times 12) + b^{2} \\ 400 & = & 144 + b^{2} \end{array} \end{aligned}

202=(12)2+b2(20x20)=(12x12)+b2400=144+b2

Next, subtract 144 from both sides of the equation to isolate the variable and simplify both sides of the equation.
::接下来,从方程的两侧减去144,以孤立变量并简化方程的两侧。

\begin{aligned} \begin{array}{rcl} 400 & = & 144 + b^{2} \\ 400 - 144 & = & 144 - 144 + b^{2} \\ 256 & = & b^{2} \end{array} \end{aligned}

::400=144+b2400-144=144-144+b2256=b2

Then, solve for ‘b’ by taking the square root of both sides of the equation. Remember taking the square root is the inverse operation of squaring .
::然后,用方程式两侧的平方根解决 'b' 。记住以正方根解决是方程式的反作用。

\begin{aligned} \begin{array}{rcl} 256 & = & b^{2} \\ \sqrt{256} & = & \sqrt{b^{2}} \\ 16 & = & b \end{array} \end{aligned}

::256=b2256=b216=b

The answer is 16.
::答案是16岁

The length of side ‘ $\begin{aligned} b \end{aligned}$ ’ is 16 inches.
::侧边的 " b " 长度为16英寸。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Tracy and her rescue mission. She needs to know if the ladder she is using is long enough to rescue her kitten.
::她需要知道她使用的梯子是否足够长的时间去救她的小猫

First, draw and label a picture to model the problem.
::首先,绘制图片并贴上标签来模拟问题。

Next, look at the right triangle and determine the measurements of the two known sides.
::接下来,看看正确的三角形并确定对已知两边的测量结果

$\begin{aligned} a = 3.8 yards \end{aligned}$
::a=3.8码

$\begin{aligned} b = 0.7 yards \end{aligned}$
::b=0.7码

Next, use the Pythagorean Theorem to calculate the length of the ladder which is the hypotenuse of the right triangle.
::接下来,使用 Pythagoren 理论来计算阶梯的长度, 即右三角形的下限。

\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}

::c2=a2+b2 (千兆赫)

First, fill in the values for ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ . ’
::首先,填充“a”和“b”的值。

\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ c^{2} & = & (3.8)^{2} + (0.7)^{2} \end{array} \end{aligned}

::c2=a2+b2c2=(3.8)2+(0.7)2

Next, perform the indicated operations and simplify the equation.
::下一步,执行所述行动并简化方程式。

\begin{aligned} \begin{array}{rcl} c^{2} & = & (3.8 \times 3.8) + (0.7 \times 0.7) \\ c^{2} & = & 14.44 + 0.49 \\ c^{2} & = & 14.93 yards \end{array} \end{aligned}

::c2=(3.8x3.8)+(0.7x0.7)c2=14.44+0.0.49c2=14.93码

Then, solve for ‘ $\begin{aligned} c \end{aligned}$ ’ by taking the square root of each side of the equation.
::然后,用方程式每侧的平方根解决“c”问题。

\begin{aligned} \begin{array}{rcl} c^{2} & = & 14.93 \\ \sqrt{c^{2}} & = & \sqrt{14.93} \\ c & = & 3.86 \end{array} \end{aligned}

The answer is 3.86.
::c2=14.93c2=14.93c=3.86 答案是3.86

The ladder must be 3.86 yards in length to rescue the kitten. The ladder Tracy is using is long enough.
::梯子必须长3.86码才能救小猫特蕾西用的梯子足够长了

Example 2
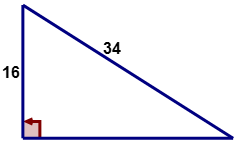
::例2

Use the Pythagorean Theorem to calculate the length of the missing side of the following right triangle:
::使用 Pytagorean 理论来计算以下右三角形的缺失侧的长度 :

First, determine what the given values represent and what side is missing?
::首先, 确定给定值代表什么, 缺少哪一边 ?

$\begin{aligned} a = 16 \end{aligned}$
::a=16

$\begin{aligned} b = ? \end{aligned}$
::b== ? 吗?

$\begin{aligned} c = 34 \end{aligned}$
::c=34 =34

Next, substitute the given values into equation that represents the Pythagorean Theorem.
::接下来,将给定值替换为代表毕达哥伦神话的方程。

\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (34)^{2} & = & (16)^{2} + b^{2} \end{array} \end{aligned}

::c2=a2+b2(342)=(162+b2)

Next, perform the indicated operations on both sides of the equation.
::接下来,在等式的两侧执行指示的行动。

\begin{aligned} \begin{array}{rcl} (34)^{2} & = & (16)^{2} + b^{2} \\ (34 \times 34) & = & (16 \times 16) + b^{2} \\ 1156 & = & 256 + b^{2} \end{array} \end{aligned}

342=(166)2+b2(34x34)=(16x16)+b21156=256+b2)

Next, subtract 256 from both sides of the equation to isolate the variable.
::接下来,从方程的两侧减去256,以孤立变量。

\begin{aligned} \begin{array}{rcl} 1156 & = & 256 + b^{2} \\ 1156 - 256 & = & 256 - 256 + b^{2} \end{array} \end{aligned}

::1156=256+b21156-256=256=256-256+b2

Next, simplify the equation.
::接下来,简化方程

\begin{aligned} \begin{array}{rcl} 1156 - 256 & = & 256 - 256 + b^{2} \\ 900 & = & b^{2} \end{array} \end{aligned}

::1156-256=256-256+b2900=b2

Then, take the square root of both sides of the equation to solve for the variable ‘b.’
::然后,选择方程式两侧的平方根,解决变量“b”的正方根。

\begin{aligned} \begin{array}{rcl} 900 & = & b^{2} \\ \sqrt{900} & = & \sqrt{b^{2}} \\ 30 & = & b \end{array} \end{aligned}

The answer is

\begin{aligned} b = 30 \end{aligned}

.
::900=b2900=b230=b 答案是b=30

Example 3
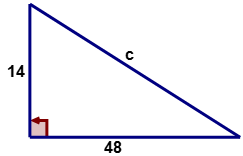
::例3

Find the length of the hypotenuse of a right triangle given the lengths of legs ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ ’ are 14 and 48 centimeters, respectively.
::找到右三角形的下限长度, 因为腿“a”和“b”的长度分别为14厘米和48厘米。

First, draw and label a right triangle to represent the given information.
::首先,绘制并标出一个右三角形以代表给定的信息。

Next, substitute the given values into equation that represents the Pythagorean Theorem.
::接下来,将给定值替换为代表毕达哥伦神话的方程。

\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ c^{2} & = & (14)^{2} + (48)^{2} \end{array} \end{aligned}

::c2=a2+b2c2=(14)2+(48)2

Next, perform the indicated operations and simplify the equation.
::下一步,执行所述行动并简化方程式。

\begin{aligned} \begin{array}{rcl} c^{2} & = & (14)^{2} + (48)^{2} \\ c^{2} & = & (14 \times 14)^{2} + (48 \times 48)^{2} \\ c^{2} & = & 196 + 2304 \end{array} \end{aligned}

::c2=(14)2+(482c2=(14x14)2+(48x482c2=196+2304)

Next, simplify the equation by adding the values on the right side of the equation.
::下一步,简化方程式,在方程式右侧添加值。

\begin{aligned} \begin{array}{rcl} c^{2} & = & 196 + 2304 \\ c^{2} & = & 2500 \end{array} \end{aligned}

::c2=196+2304c2=2500

Then, take the square root of both sides of the equation to solve for the variable ‘ $\begin{aligned} c \end{aligned}$ .’
::然后,选择方程两侧的平方根,解决变量“c”的正方根。

\begin{aligned} \begin{array}{rcl} c^{2} & = & 2500 \\ \sqrt{c^{2}} & = & 2500 \\ c & = & 50 \end{array} \end{aligned}

::c2=2500c2=2500c=50

The answer is $\begin{aligned} c = 50 \end{aligned}$ .
::答案是C=50。

The length of the hypotenuse is 50 cm.
::下限长度为50厘米。

Example 4
::例4

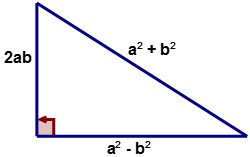
If ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ ’ are values such that $\begin{aligned} a, b \in N \end{aligned}$ and $\begin{aligned} a > b \end{aligned}$ then the sides of a right triangle are $\begin{aligned} a^{2} + b^{2} \end{aligned}$ , $\begin{aligned} a^{2} - b^{2} \end{aligned}$ , and $\begin{aligned} 2 a b \end{aligned}$ as shown in the diagram below.
::如果 " a " 和 " b " 值为a、bN和a>b等值,则右三角形的侧面为a2+b2、a2-b2和2ab,如下图所示。

Complete the following table to generate Pythagorean Triples.
::完成下表以生成毕达哥伦三角形。

$\begin{aligned} a \end{aligned}$	$\begin{aligned} b \end{aligned}$	$\begin{aligned} a^{2} - b^{2} \end{aligned}$	$\begin{aligned} 2 a b \end{aligned}$	$\begin{aligned} a^{2} + b^{2} \end{aligned}$
4	2	12	16	20
5	3	16	30	34
6	4	20	48	52

First, using $\begin{aligned} a = 4 \end{aligned}$ and $\begin{aligned} b = 2 \end{aligned}$ evaluate $\begin{aligned} a^{2} - b^{2} \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=4 和 b=2 来评估 a2-b2, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} a^{2} - b^{2} \\ (4)^{2} - (2)^{2} \end{array} \end{aligned}

::a2-b2(4)2-(2)2

Next, perform the indicated operations and simply the expression.
::下一步,执行指定的操作,仅用表达方式。

\begin{aligned} \begin{array}{rcl} (4)^{2} - (2)^{2} \\ (4 \times 4) - (2 \times 2) \\ 16 - 4 \\ 12 \end{array} \end{aligned}

The answer is 12.
:

4)2-(2)2(4x4)-(2x2)16-412 答案是12。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

Now, complete the $\begin{aligned} a^{2} - b^{2} \end{aligned}$ column for the remaining given values of ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ .’
::现在,填写 " a " 和 " b " 其余给定值的 A2-b2 列。

First, using $\begin{aligned} a = 5 \end{aligned}$ and $\begin{aligned} b = 3 \end{aligned}$ evaluate $\begin{aligned} a^{2} - b^{2} \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=5 和 b=3 来评估 a2-b2, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} a^{2} - b^{2} \\ (5)^{2} - (3)^{2} \end{array} \end{aligned}

::a2-2-b2(5)2-(3)2

Next, perform the indicated operations and simply the expression.
::下一步,执行指定的操作,仅用表达方式。

\begin{aligned} \begin{array}{rcl} (5)^{2} - (3)^{2} \\ (5 \times 5) - (3 \times 3) \\ 25 - 9 \\ 16 \end{array} \end{aligned}

The answer is 16.
:

5)2-(3)2(5x5)-(3x3)25-916 答案是16。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

First, using $\begin{aligned} a = 6 \end{aligned}$ and $\begin{aligned} b = 4 \end{aligned}$ evaluate $\begin{aligned} a^{2} - b^{2} \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=6 和 b=4 来评估 a2-b2, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} a^{2} - b^{2} \\ (6)^{2} - (4)^{2} \end{array} \end{aligned}

::a2-2-b2(6)-2-4(4)2

Next, perform the indicated operations and simply the expression.
::下一步,执行指定的操作,仅用表达方式。

\begin{aligned} \begin{array}{rcl} (6)^{2} - (4)^{2} \\ (6 \times 6) - (4 \times 4) \\ 36 - 16 \\ 20 \end{array} \end{aligned}

The answer is 20.
::答案是20岁

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

First, using $\begin{aligned} a = 4 \end{aligned}$ and $\begin{aligned} b = 2 \end{aligned}$ evaluate $\begin{aligned} 2 a b \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=4 和 b=2 来评估 2ab, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} 2 a b \\ 2 (4) (2) \end{array} \end{aligned}

::2AB2(4)(2)

Next, perform the indicated operations.

\begin{aligned} \begin{array}{rcl} 2 (4) (2) \\ 8 (2) \\ 16 \end{array} \end{aligned}

The answer is 16.
::下一步,执行指定的行动。 2(4)(2)8(2)16 答案是16。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

Now, complete the 2ab column for the remaining given values of ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘b.’
::现在,为剩余给定值`a ' 和`b'填写 2ab 列。

First, using $\begin{aligned} a = 5 \end{aligned}$ and $\begin{aligned} b = 3 \end{aligned}$ evaluate $\begin{aligned} 2 a b \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=5 和 b=3 来评估 2ab, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} 2 a b \\ 2 (5) (3) \end{array} \end{aligned}

::2ab2(5)(3)

Next, perform the indicated operations.
::下一步,执行所述行动。

\begin{aligned} \begin{array}{rcl} 2 (5) (3) \\ 10 (3) \\ 30 \end{array} \end{aligned}

The answer is 30.
::2(5)(3)10(3)30 答案是30。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

First, using $\begin{aligned} a = 6 \end{aligned}$ and $\begin{aligned} b = 4 \end{aligned}$ evaluate $\begin{aligned} 2 a b \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=6 和 b=4 来评估 2ab, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} 2 a b \\ 2 (6) (4) \end{array} \end{aligned}

::2ab2(6)(4)

Next, perform the indicated operations.
::下一步,执行所述行动。

\begin{aligned} \begin{array}{rcl} 2 (6) (4) \\ 12 (4) \\ 48 \end{array} \end{aligned}

The answer is 48.
::2(6)(4)12(4)48 答案是48。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

First, using $\begin{aligned} a = 4 \end{aligned}$ and $\begin{aligned} b = 2 \end{aligned}$ evaluate $\begin{aligned} a^{2} + b^{2} \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=4 和 b=2 来评估 a2+b2, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} a^{2} + b^{2} \\ (4)^{2} (2)^{2} \end{array} \end{aligned}

::a2+b2(4)2(2)2

Next, perform the indicated operations and simply the expression.
::下一步,执行指定的操作,仅用表达方式。

\begin{aligned} \begin{array}{rcl} (4)^{2} + (2)^{2} \\ (4 \times 4) + (2 \times 2) \\ 16 + 4 \\ 20 \end{array} \end{aligned}

The answer is 20.
::答案是20岁

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

Now, complete the $\begin{aligned} a^{2} + b^{2} \end{aligned}$ column for the remaining given values of ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ .’
::现在,为剩余给定值`a ' 和`b'填写 a2+b2列。

First, using $\begin{aligned} a = 5 \end{aligned}$ and $\begin{aligned} b = 3 \end{aligned}$ evaluate $\begin{aligned} a^{2} + b^{2} \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=5 和 b=3 来评估 a2+b2, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} a^{2} + b^{2} \\ (5)^{2} + (3)^{2} \end{array} \end{aligned}

::a2+b2(5)2+(3)2

Next, perform the indicated operations and simply the expression.
::下一步,执行指定的操作,仅用表达方式。

\begin{aligned} \begin{array}{rcl} (5)^{2} + (3)^{2} \\ (5 \times 5) + (3 \times 3) \\ 25 + 9 \\ 34 \end{array} \end{aligned}

The answer is 34.
:

5)2+(3)2(5x5)+(3x3)25+934 答案是34。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

First, using $\begin{aligned} a = 6 \end{aligned}$ and $\begin{aligned} b = 4 \end{aligned}$ evaluate $\begin{aligned} a^{2} + b^{2} \end{aligned}$ by substituting the given values into the expression.
::首先,使用 a=6 和 b=4 来评估 a2+b2, 将给定值替换为表达式。

\begin{aligned} \begin{array}{rcl} a^{2} + b^{2} \\ (6)^{2} + (4)^{2} \end{array} \end{aligned}

::a2+b2(6)2+(4)2

Next, perform the indicated operations and simply the expression.
::下一步,执行指定的操作,仅用表达方式。

\begin{aligned} \begin{array}{rcl} (6)^{2} + (4)^{2} \\ (6 \times 6) + (4 \times 4) \\ 36 + 16 \\ 52 \end{array} \end{aligned}

The answer is 52.
:

6)2+(4)2(26x6)+(4x4)36+1652 答案是52。

Then, place the answer in the table in the correct column.
::然后,将答案放在表格中正确的一列。

Example 5
::例5

Use the Pythagorean Theorem to find the length of the missing leg of the following right triangle.
::使用 Pytagorean Theorem 来查找以下右三角形缺失的腿长度。

First, determine what the given values represent and what side is missing?
::首先, 确定给定值代表什么, 缺少哪一边 ?

$\begin{aligned} a = ? \end{aligned}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么?

$\begin{aligned} b = 10 \end{aligned}$
::b=10 (b=10)

$\begin{aligned} c = 26 \end{aligned}$
::c=26 (c=26)

Next, substitute the given values into equation that represents the Pythagorean Theorem.
::接下来,将给定值替换为代表毕达哥伦神话的方程。

\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (26)^{2} & = & a^{2} + (10)^{2} \end{array} \end{aligned}

::c2=a2+b2(262)=a2+(10)2

Next, perform the indicated operations and simplify the equation.
::下一步,执行所述行动并简化方程式。

\begin{aligned} \begin{array}{rcl} (26)^{2} & = & a^{2} + (10)^{2} \\ (26 \times 26) & = & a^{2} + (10 \times 10) \\ 676 & = & a^{2} + 100 \end{array} \end{aligned}

262=a2+(10)2(26x26)=a2+(10x10)10)676=a2+100)

Next, subtract 100 from both sides of the equation to isolate the variable.
::接下来,从方程两侧减去100,以孤立变量。

\begin{aligned} \begin{array}{rcl} 676 & = & a^{2} + 100 \\ 676 - 100 & = & a^{2} + 100 - 100 \end{array} \end{aligned}

::676=a2+100676-100=a2+100-100

Next, simplify the equation.
::接下来,简化方程

\begin{aligned} \begin{array}{rcl} 676 - 100 & = & a^{2} + 100 - 100 \\ 576 & = & a^{2} \end{array} \end{aligned}

::676-100=a2+100-100576=a2

Then, take the square root of both sides of the equation to solve for the variable ‘ $\begin{aligned} a \end{aligned}$ .’
::然后,用方程式两边的平方根解决变量“a.”的问题。

\begin{aligned} \begin{array}{rcl} 576 & = & a^{2} \\ \sqrt{576} & = & \sqrt{a^{2}} \\ 24 & = & a \end{array} \end{aligned}

The answer is

\begin{aligned} a = 24 \end{aligned}

.
::576=a2576=a224=a 答案是a=24。

Review
::回顾

Use the Pythagorean Theorem to find the missing dimensions of each right triangle.
::使用 Pytagorean 理论来查找每个右三角形的缺失维度。

1. $\begin{aligned} a = 3, b = 4, c = ? \end{aligned}$
::1. a=3,b=4,c=?

2. $\begin{aligned} a = 6, b = 8, c = ? \end{aligned}$
::2. a=6,b=8,c=?

3. $\begin{aligned} a = 9, b = 12, c = ? \end{aligned}$
::3. a=9,b=12,c=9,b=12,c=9,b=12?

4. $\begin{aligned} a = 27, b = 36, c = ? \end{aligned}$
::4. a=27,b=36,c=?

5. $\begin{aligned} a = 15, b = 20, c = ? \end{aligned}$
::5. a=15,b=20,c=?

6. $\begin{aligned} a = 18, b = 24, c = ? \end{aligned}$
::6. a=18,b=24,c=?

7. $\begin{aligned} a = ?, b = 16, c = 20 \end{aligned}$
::7.a=? b=16,c=20

8. $\begin{aligned} a = ?, b = 28, c = 35 \end{aligned}$
::8. a=? b=28,c=35

9. $\begin{aligned} a = 30, b = ?, c = 50 \end{aligned}$
::9. a=30,b=? c=50

10. $\begin{aligned} a = 33, b = ?, c = 55 \end{aligned}$
::10. a=33,b=? c=55

11. $\begin{aligned} a = 1.5, b = ?, c = 2.5 \end{aligned}$
::11. a=1.5,b=? c=2.5

12. $\begin{aligned} a = 36, b = ?, c = 60 \end{aligned}$
::12. a=36,b=? c=60

State whether the following statements are True or False.
::说明以下声明是真实的还是虚假的。

13. The Pythagorean Theorem will work for any triangle.
::13. 毕达哥里安理论将为任何三角形工作。

14. The longest side of a right triangle is called the hypotenuse.
::14. 右三角形最长的一面称为下限。

15. A Pythagorean Triple can only be found in a right triangle.
::15. 唯有在右三角内才能找到毕达哥伦三角形。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

提取并使用毕达哥里定理

Pythagorean Theorem ::毕达哥里安神论

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Pythagorean Theorem
::毕达哥里安神论

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)