7.9 毕达哥里安理论、周边和地区

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 毕达哥里安理论、周边和地区

  Collapse Expand

  毕达哥里安理论、周边和地区

  

  播放段落

  The Art class has decided on a project to add some character to the school. Instead of mounting signs to name the various departments of the school, they have decided to paint unique pictures to indicate the various departments. For the Math Department they are going to paint a picture of Pythagoras on canvas shaped as a right triangle and frame it. If the measurements of the right triangle canvas are $\begin{align*}(5, 12, ?)\end{align*}$  inches, how could Pythagoras help the students to calculate the area of the canvas on which they are painting and the number of inches of framing wood needed?
  ::艺术课决定在学校增加一些字符。 他们决定为学校各部门命名一个项目, 而不是挂上标志来命名学校各部门, 他们决定绘制独特的图片来标示各部门。 对于数学系, 他们将用画布来绘制像右三角形形状的比达哥拉斯画像, 并框框它。 如果对右三角形画布的测量是( 5, 12,? ? ) 英寸, 皮达哥拉斯如何帮助学生计算他们画画的画布面积和需要的木板英寸数 ?

  播放段落

  In this concept, you will learn to use the Pythagorean Theorem to find area and perimeter .
  ::在这个概念中,你将学会使用毕达哥里安神话 寻找地区和周边

  播放段落

  Perimeter and Area
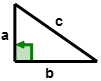
  ::周边和面积

  播放段落

  The perimeter of a shape is the distance around the outside of the shape. Perimeter is 1-dimensional and is measured in linear units. If a rectangular enclosure is being built for a dog, then the shape is two-dimensional since it has both length and width. The amount of fencing to go around the enclosure is one-dimensional since it is the sum of the lengths of the four sides of the rectangle .
  ::形状的周边是形状外侧的距离。 周围是一维的, 用线性单位测量。 如果正在为一只狗建造长方形围框, 则形状是二维的, 因为它有长度和宽度。 围圈周围的栅栏数量是一维的, 因为它是矩形四侧长度的和。

  播放段落

  The perimeter of a right triangle is the sum of the lengths of the two legs and the hypotenuse . The perimeter could be written as:
  ::右三角形的周界是两条腿和下限长度的总和。

  播放段落

  $$\begin{align*}P_{(\text{right } \Delta)} = a + b + c\end{align*}$$
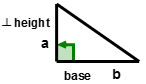
  ::P( Right ) = a+b+c

  

  播放段落

  The area of a plane shape is the size of its surface. Area is a two-dimensional measurement and is expressed in square units . The area of a triangle is one-half the product of its base and its perpendicular height . The formula for finding the area of a triangle is written as:
  ::平面形状的面积是其表面的大小。区域是二维测量,以平方单位表示。三角形的面积是其底部和垂直高度的半份产物。查找三角形区域的公式写法为:

  播放段落

  $$\begin{align*}A_{\text{triangle}} = \frac{1}{2} b \cdot h\end{align*}$$
  ::三角形= 12bh

  播放段落

  For the area of a right triangle , the product of the base and its perpendicular height is the product of its two legs ‘ $\begin{align*}a\end{align*}$ ’ and ‘ $\begin{align*}b\end{align*}$ ’. The formula for finding area of a right triangle could be written as:
  ::对于右三角的面积,基座的产物及其垂直高度是其两条腿“a”和“b”的产物。

  播放段落

  $$\begin{align*}A_{(\text{right } \Delta)} = \frac{1}{2} a \cdot b\end{align*}$$
  ::A(右 )= 12ab

  

  播放段落

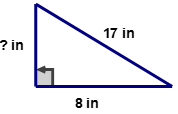
  Find the perimeter and the area of the following right triangle.
  ::查找以下右三角形的周界和地区。

  

  播放段落

  Remember the perimeter is the sum of the lengths of the two legs and the hypotenuse. The length of one of the legs is unknown. Use the Pythagorean Theorem to find the length of ‘ $\begin{align*}a\end{align*}$ .’
  ::记住, 周界是两条腿的长度和下肢的长度之和。 其中一条腿的长度未知。 使用 Pytagoren 理论来找到“ a ” 的长度 。

  播放段落

  First, determine the values for $\begin{align*}(a, b, c)\end{align*}$  of the Pythagorean Theorem.
  ::首先,确定毕达哥里安神话(a、b、c)的值。

  播放段落

  $$\begin{align*}\begin{array}{rcl} a &=& ?\\ b &=& 8\\ c &=& 17 \end{array}\end{align*}$$
  ::a=? b=8c=17

  播放段落

  Next, substitute the values for $\begin{align*}(a, b, c)\end{align*}$  into the Pythagorean Theorem.
  ::其次,将数值(a,b,c)替换为毕达哥里安神话。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2\\ (17)^2 &=& a^2 + (8)^2 \end{array}\end{align*}$$
  ::c2=a2+b2(172)=a2+(8)2

  播放段落

  Next, perform the indicated squaring and simplify the equation.
  ::下一步,执行指示的对角并简化方程。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (17)^2 &=& a^2 + (8)^2\\ (17 \times 17) &=& a^2 + (8 \times 8)\\ 289 &=& a^2 + 64 \end{array}\end{align*}$$
  :172=a2+a2+(8)2(17x17)=a2+(8x8)289=a2+64)

  播放段落

  Next, isolate the variable by subtracting 64 from both sides of the equation.
  ::接下来,从方程的两侧减去64,将变量分离出来。

  播放段落

  $$\begin{align*}\begin{array}{rcl} 289 &=& a^2 + 64\\ 289 - 64 &=& a^2 + 64 - 64\\ 225 &=& a^2 \end{array}\end{align*}$$
  ::289=a2+64289-64=a2+64-64225=a2

  播放段落

  Then, solve for the variable ‘ $\begin{align*}a\end{align*}$ ’ by taking the square root of both sides of the equation.
  ::然后,用方程式两侧的平方根解决变量“a”。

  播放段落

  $$\begin{align*}\begin{array}{rcl} 225 &=& a^2\\ \sqrt{225} &=& \sqrt{a^2}\\ 15 &=& a \end{array}\end{align*}$$
  ::225=a225=a215=a

  播放段落

  The answer is 15.
  ::答案是15岁

  播放段落

  The length of leg ‘ $\begin{align*}a\end{align*}$ ’ is 15 inches.
  ::" a " 腿长15英寸。

  播放段落

  Now that the length of all the sides of the triangle are known, substitute the values into the equation for finding the perimeter of the triangle.
  ::现在三角形所有侧面的长度已经为人所知, 将数值替换为方程中找到三角形周边的值 。

  播放段落

  $$\begin{align*}\begin{array}{rcl} P_{(\text{right } \Delta)} &=& a + b + c\\ P_{(\text{right } \Delta)} &=& 15 + 8 + 17\\ P_{(\text{right } \Delta)} &=& 40 \end{array}\end{align*}$$
  ::P( Right ) = a+b+cP( Right ) = 15+8+17P( Right ) = 40

  播放段落

  The answer is 40.
  ::答案是40岁

  播放段落

  The perimeter of the right triangle is 40 inches.
  ::右三角的周边是40英寸

  播放段落

  Now that the lengths of both legs are known, substitute the values into the formula to determine the area of the right triangle.
  ::现在双腿的长度已经为人所知, 将值替换为公式, 以决定右三角形的面积 。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A_{(\text{right } \Delta)} &=& \frac{1}{2} a \cdot b\\ A_{(\text{right } \Delta)} &=& \frac{1}{2} (15)(8) \end{array}\end{align*}$$
  :右)=12a&bA(右)=12(15)(8)

  播放段落

  Next, perform the indicated operations on the right side of the equation.
  ::下一步,在方程右侧执行指定的操作。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A_{(\text{right } \Delta)} &=& \frac{1}{2} (15)(8)\\ A_{(\text{right } \Delta)} &=& \frac{1}{2} (120)\\ A_{(\text{right } \Delta)} &=& 60 \end{array}\end{align*}$$
  ::A(右) = 12(15) 8 A(右) = 12(120) A(右) = 60

  播放段落

  The answer is 60.
  ::答案是60岁

  播放段落

  The area of the right triangle is 60 in ² .
  ::右三角形的面积是60英寸2。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about  the Art class and their unique signs. The students need to find the area of the triangular canvas and the wood needed for the frame.
  ::早些时候,你曾遇到艺术课及其独特标志的问题。 学生们需要找到三角帆布的面积和框架所需的木头。

  播放段落

  First, the students know the measurements for the two legs of the right triangle. The given values for $\begin{align*}(a, b, c)\end{align*}$  of the Pythagorean Theorem are $\begin{align*}(5, 12, c)\end{align*}$ .
  ::首先,学生们知道右三角的两条腿的测量方法。Pytagoren神话(a,b,c)的给定值是(5,12,c)。

  播放段落

  Next, use the formula for finding the area of a right triangle to determine the area of the canvas.
  ::接下来,使用查找右三角形区域的公式来确定画布的面积。

  播放段落

  $$\begin{align*}A_{(\text{right } \Delta)} = \frac{1}{2} a \cdot b\end{align*}$$
  ::A(右 )= 12ab

  播放段落

  Next, fill in the values for ‘ $\begin{align*}a\end{align*}$ ’ and ‘ $\begin{align*}b\end{align*}$ ’ into the formula.
  ::接下来,填入公式中的 'a ' 和 'b ' 的值。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A_{(\text{right } \Delta)} &=& \frac{1}{2} a \cdot b\\ A_{(\text{right } \Delta)} &=& \frac{1}{2} (5)(12) \end{array}\end{align*}$$
  ::A( 右 ) = 12abA( 右 ) = 12(5)( 12)

  播放段落

  Then, perform the operations on the right side of the equation.
  ::然后在方程的右侧执行操作。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A_{(\text{right } \Delta)} &=& \frac{1}{2} (5)(12)\\ A_{(\text{right } \Delta)} &=& \frac{1}{2} (60)\\ A_{(\text{right } \Delta)} &=& 30 \end{array}\end{align*}$$
  ::A(权利)=12(5)(12)A(权利)=12(60)A(权利)=30

  播放段落

  The answer is 30.
  ::答案是30岁

  播放段落

  The area of the canvas is 30 in ² .
  ::画布的面积是30英寸2

  播放段落

  The amount of wood needed to frame the painting is the perimeter of the right triangle. Use the Pythagorean Theorem to find the length of ‘ $\begin{align*}c\end{align*}$ .’ This is the hypotenuse of the canvas.
  ::绘制画框所需的木柴数量是右三角的周界。 使用 Pythagorena 理论查找 ' c. ' 的长度 。 这是画布的下限值 。

  播放段落

  $$\begin{align*}c^2 = a^2 + b^2\end{align*}$$
  ::c2=a2+b2 (千兆赫)

  播放段落

  Next, fill in the values for ‘ $\begin{align*}a\end{align*}$ ’ and ‘ $\begin{align*}b\end{align*}$ ’ in the Pythagorean Theorem.
  ::接下来,填充《毕达哥里安神话》中的“a”和“b”的值。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2\\ c^2 &=& (5)^2 + (12)^2 \end{array}\end{align*}$$
  ::c2=a2+b2c2=(5)2+(12)2

  播放段落

  Next, perform the indicated squaring and simplify the right side of the equation.
  ::下一步,执行指示的对角并简化方程的右侧。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& (5)^2 + (12)^2\\ c^2 &=& 25 + 144\\ c^2 &=& 169 \end{array}\end{align*}$$
  ::c2=(5)2+(12)2c2=25+144c2=169

  播放段落

  Then, solve for the variable ‘ $\begin{align*}c\end{align*}$ ’ by taking the square root of both sides of the equation.
  ::然后,用方程式两侧的平方根解决变量“c”。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& 169\\ \sqrt{c^2} &=& \sqrt{169}\\ c &=& 13 \end{array}\end{align*}$$
  ::c2=169=c2=c2=c1=13=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=c2=13

  播放段落

  The answer is 13.
  ::答案是13岁

  播放段落

  The length of the hypotenuse is 13 inches.
  ::下限长度是13英寸

  播放段落

  Next, find the perimeter of the canvas using the formula:
  ::接下来,用公式找到画布的周界:

  播放段落

  $$\begin{align*}P_{(\text{right } \Delta)} = a + b + c\end{align*}$$
  ::P( Right ) = a+b+c

  播放段落

  Next, fill in the values $\begin{align*}(5, 12, 13)\end{align*}$  for $\begin{align*}(a, b, c)\end{align*}$  and find the sum of the values.
  ::然后填入(a,b,c)的数值(5,12,13),并找到数值的总和。

  播放段落

  $$\begin{align*}\begin{array}{rcl} P_{(\text{right } \Delta)} &=& a + b + c\\ P_{(\text{right } \Delta)} &=& 5 + 12 + 13\\ P_{(\text{right } \Delta)} &=& 30 \end{array}\end{align*}$$
  ::P( Right ) = a+b+cP( Right ) = 5+12+13P( Right ) =30

  播放段落

  The answer is 30.
  ::答案是30岁

  播放段落

  The amount of wood needed for framing the picture is 30 inches.
  ::绘制图象所需的木材量为30英寸。

  播放段落

  Example 2
  ::例2

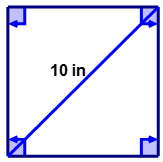
  播放段落

  A square sheet of corrugated cardboard has a perforated diagonal measuring 10 inches in length. Find the area of the square.
  ::圆形纸板的平方板有穿孔的对角长度为10英寸。 查找方形的区域 。

  播放段落

  First, draw and label a diagram to model the problem.
  ::首先,绘制并标注一个图表来模拟问题。

  

  播放段落

  The diagonal divides the square into two equal right triangles. Remember the sides of a square are all equal in length. The Pythagorean Theorem can be used to find the length of the sides of the square.
  ::对角线将方形分割为两个对等右三角形。 记住方形的两边长度相等。 平面的定理可以用来查找方形两边的长度 。

  播放段落

  First, write the equation that models the Pythagorean Theorem.
  ::首先,写出比达哥伦神话模型的方程式

  播放段落

  $$\begin{align*}c^2 = a^2 + b^2\end{align*}$$
  ::c2=a2+b2 (千兆赫)

  播放段落

  Next, rewrite the equation to indicate $\begin{align*}a^2 = b^2\end{align*}$ .
  ::下一步,重写方程式以表示 a2=b2。

  播放段落

  $$\begin{align*}c^2 = a^2 + a^2\end{align*}$$
  ::c2=a2+a2 (千兆赫)

  播放段落

  Next, simplify the right side of the equation by combining the like terms.
  ::接下来,简化方程式的右侧, 将类似条件合并 。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + a^2\\ c^2 &=& 2a^2 \end{array}\end{align*}$$
  ::c2=a2+a2c2=2a2

  播放段落

  Next, substitute $\begin{align*}c=10\end{align*}$  into the equation.
  ::下一个,在方程中替换 C=10。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& 2a^2\\ (10)^2 &=& 2a^2 \end{array}\end{align*}$$
  ::c2=2a2(10.2)2=2a2

  播放段落

  Next, perform the indicated squaring.
  ::接下来,进行标注的对角。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (10)^2 &=& 2a^2\\ (10 \times 10) &=& 2a^2\\ 100 &=& 2a^2 \end{array}\end{align*}$$
  :10)2=2a2(10x10)=2a2100=2a2

  播放段落

  Next, isolate the variable by dividing both sides of the equation by 2.
  ::接下来,通过将方程两侧除以 2 来孤立变量。

  播放段落

  $$\begin{align*}\begin{array}{rcl} 100 &=& 2a^2\\ \frac{100}{2} &=& \frac{\overset{{1}}{\cancel{2}}a^2}{\cancel{2}}\\ 50 &=& a^2 \end{array}\end{align*}$$
  ::100=2a21002=12a2250=a2

  播放段落

  Then, solve for the variable ‘ $\begin{align*}a\end{align*}$ ’ by taking the square root of both sides of the equation.
  ::然后,用方程式两侧的平方根解决变量“a”。

  播放段落

  $$\begin{align*}\begin{array}{rcl} 50 &=& a^2\\ \sqrt{50} &=& \sqrt{a^2}\\ 7.07 &=& a \end{array}\end{align*}$$
  ::50=a250a27.07=a

  播放段落

  The answer is 7.07.
  ::答案是7.07。

  播放段落

  The length of each side of the square is 7.07 inches.
  ::方形每一侧的长度为7.07英寸。

  播放段落

  The area of a square is found by using the formula:
  ::方形区域使用公式查找:

  播放段落

  $\begin{align*}A=s^2\end{align*}$  where ‘ $\begin{align*}s\end{align*}$ ’ represents the side length of the square.
  ::A=2,其中 's ' 表示方形的侧长。

  播放段落

  First, fill in the side length of 7.07 into the formula.
  ::首先,在公式中填充7.07的侧长。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A &=& s^2\\ A &=& (7.07)^2 \end{array}\end{align*}$$
  ::A=S2A=(7.077)2

  播放段落

  Then, perform the indicated squaring and simplify the equation. Round your answer to the nearest square inch.
  ::然后,执行指示的方程并简化方程。 将答案绕到最接近的平方英寸处。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A &=& (7.07)^2\\ A &=& (7.07 \times 7.07)\\ A &=& 49.98\\ A &=& 50 \end{array}\end{align*}$$
  ::A=(7.077)2A=(7.07x7.07)A=49.98A=50

  播放段落

  The answer is 50.
  ::答案是50

  播放段落

  The area of the square is 50 in ² .
  ::广场面积为50英寸2。

  播放段落

  Example 3
  ::例3

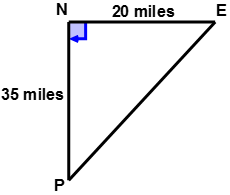
  播放段落

  A ship leaves port and sails 35 miles due north and then 20 miles due east. If the ship returns to port by travelling along the diagonal route, how many miles would the ship have sailed altogether?
  ::一艘船舶离港35英里,北面35英里,东面20英里。 如果该船沿对角航线返回港口,该船总共会航行多少英里?

  播放段落

  First, draw and label a diagram to model the problem.
  ::首先,绘制并标注一个图表来模拟问题。

  

  播放段落

  First, use the Pythagorean Theorem to find the distance from east to port.
  ::首先,利用毕达哥里安神话 找到从东到港的距离

  播放段落

  $$\begin{align*}c^2 = a^2 + b^2\end{align*}$$
  ::c2=a2+b2 (千兆赫)

  播放段落

  Next, determine the values of $\begin{align*}(a, b, c)\end{align*}$  for the Pythagorean Theorem.
  ::下一步,为毕达哥里安神话确定(a、b、c)值。

  播放段落

  $$\begin{align*}\begin{array}{rcl} a &=& 35 \text{ miles} = 35\\ b &=& 20 \text{ miles} = 20\\ c &=& ? \text{ miles} \ \ = c \end{array}\end{align*}$$ Next, fill the values into the Pythagorean Theorem.
  ::a=35英里=35b=20英里=20c=20c=?英里=下一步,将数值填入毕达哥里安理论。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2\\ c^2 &=& (35)^2 + (20)^2 \end{array}\end{align*}$$
  ::c2=a2+b2c2=(35)2+(20)2

  播放段落

  Next, perform the indicated squaring and simplify the right side of the equation.
  ::下一步,执行指示的对角并简化方程的右侧。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& (35)^2 + (20)^2\\ c^2 &=& 1225 + 400\\ c^2 &=& 1625 \end{array}\end{align*}$$
  ::c2=(35)2+(202)2c2=1225+400c2=1625

  播放段落

  Then, solve for the variable ‘ $\begin{align*}c\end{align*}$ ’ by taking the square root of both sides of the equation.
  ::然后,用方程式两侧的平方根解决变量“c”。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& 1625\\ \sqrt{c^2} &=& \sqrt{1625}\\ c &=& 40.31 \end{array}\end{align*}$$
  ::c2=1625c21625c=40.31

  播放段落

  The answer is 40.31.
  ::答案是40.31。

  播放段落

  The distance from east toport is 40.31 miles.
  ::东到港的距离是40.31英里

  播放段落

  Now, determine the total distance the ship has sailed by finding the perimeter of the right triangle.
  ::现在,通过找到右三角形的周边 确定船航行的总距离

  播放段落

  $$\begin{align*}P_{(\text{right } \Delta)} = a + b + c\end{align*}$$
  ::P( Right ) = a+b+c

  播放段落

  Next, fill in the values $\begin{align*}(35, 20, 40.31)\end{align*}$  for $\begin{align*}(a, b, c)\end{align*}$  and find the sum of the values.
  ::然后填入(a,b,c)的值(35,20,40.31),并找到数值的总和。

  播放段落

  $$\begin{align*}\begin{array}{rcl} P_{(\text{right } \Delta)} &=& a + b + c\\ P_{(\text{right } \Delta)} &=& 35 + 20 + 40.31\\ P_{(\text{right } \Delta)} &=& 95.31 \end{array}\end{align*}$$ The answer is 95.31.
  ::P(right ) = a+b+cP(right ) = 35+20+40.31P(right ) =95.31 答案是95.31。

  播放段落

  The ship will have sailed 95.31 miles.
  ::船将航行95.31英里

  播放段落

  Example 4
  ::例4

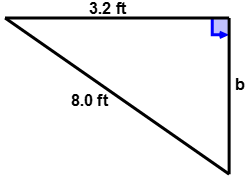
  播放段落

  Find the area of the following right triangle.
  ::查找以下右三角形的区域。

  

  播放段落

  Remember to find the area of a right triangle the lengths of the two legs must be known. Use the Pythagorean Theorem to find the length of side ‘ $\begin{align*}b\end{align*}$ .’
  ::记住要找到右三角形的面积, 必须知道两条腿的长度 。 使用 Pytagoren 理论来找到侧边“ b ” 的长度 。

  播放段落

  First, determine the values for $\begin{align*}(a, b, c)\end{align*}$  of the Pythagorean Theorem.
  ::首先,确定毕达哥里安神话(a、b、c)的值。

  播放段落

  $$\begin{align*}\begin{array}{rcl} a &=& 3.2\\ b &=& ?\\ c &=& 8 \end{array}\end{align*}$$
  ::a=3.2b=? c=8

  播放段落

  Next, substitute the values for $\begin{align*}(a, b, c)\end{align*}$  into the Pythagorean Theorem.
  ::其次,将数值(a,b,c)替换为毕达哥里安神话。

  播放段落

  $$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2\\ (8)^2 &=& (3.2)^2 + b^2 \end{array}\end{align*}$$
  ::c2=a2+b2(8)2=(3.2)2+b2

  播放段落

  Next, perform the indicated squaring and simplify the equation.
  ::下一步,执行指示的对角并简化方程。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (8)^2 &=& (3.2)^2 + b^2\\ (8 \times 8) &=& (3.2 \times 3.2) + b^2\\ 64 &=& 10.24 + b^2 \end{array}\end{align*}$$
  :8)2=(3.2)2+b2(8)(8)=(3.2×3.2)+b264=10.24+b2

  播放段落

  Next, isolate the variable by subtracting 10.24 from both sides of the equation.
  ::接下来,从方程的两侧减去10.24,将变量分离出来。

  播放段落

  $$\begin{align*}\begin{array}{rcl} 64 &=& 10.24 + b^2\\ 64 - 10.24 &=& 10.24 - 10.24 + b^2\\ 53.76 &=& b^2 \end{array}\end{align*}$$
  ::64=10.24+b264-10.24=10.24-10.24+b253.76=2

  播放段落

  Then, solve for the variable ‘ $\begin{align*}b\end{align*}$ ’ by taking the square root of both sides of the equation.
  ::然后,用方程式两侧的平方根解决变量 'b' 。

  播放段落

  $$\begin{align*}\begin{array}{rcl} 53.76 &=& b^2\\ \sqrt{53.76} &=& \sqrt{b^2}\\ 7.3 &=& b \end{array}\end{align*}$$
  ::53.76=b253.76b27.3=b

  播放段落

  The answer is 7.3.
  ::答案是7.3。

  播放段落

  The length of leg ‘ $\begin{align*}b\end{align*}$ ’ is 7.3 ft.
  ::" b " 腿长7.3英尺。

  播放段落

  Now, find the area of the right triangle using the formula: 
  ::现在,使用公式找到右三角区域 :

  播放段落

  $$\begin{align*}A_{(\text{right } \Delta)} = \frac{1}{2} a \cdot b\end{align*}$$
  ::A(右 )= 12ab

  播放段落

  Next, fill in the values for ‘ $\begin{align*}a\end{align*}$ ’ and ‘ $\begin{align*}b\end{align*}$ ’ into the formula.
  ::接下来,填入公式中的 'a ' 和 'b ' 的值。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A_{(\text{right } \Delta)} &=& \frac{1}{2} a \cdot b\\ A_{(\text{right } \Delta)} &=& \frac{1}{2} (3.2)(7.3) \end{array}\end{align*}$$
  :右)=12a_BA(右)=12(3.2(7.3)

  播放段落

  Then, perform the indicated operations on the right side of the equation.
  ::然后在方程右侧执行指示操作。

  播放段落

  $$\begin{align*}\begin{array}{rcl} A_{(\text{right } \Delta)} &=& \frac{1}{2} (3.2)(7.3)\\ A_{(\text{right } \Delta)} &=& \frac{1}{2} (23.36)\\ A_{(\text{right } \Delta)} &=& 11.68 \end{array}\end{align*}$$
  :右)=12(3.2(7.3)A(右)=12(23.36)A(右)=11.68

  播放段落

  The answer is 11.68.
  ::答案是11.68。

  播放段落

  The area of the triangle is 11.68 ft ² .
  ::三角形区域为11.68平方英尺。

  播放段落

  Review
  ::回顾

  播放段落

  Find the missing side length of each right triangle by using the Pythagorean Theorem. You may round to the nearest tenth when necessary.
  ::使用 Pytagorena 定理来查找右三角形的侧边长度。 必要时您可以绕到最近的 10 。

  播放段落

  1.  $\begin{align*}a = 10, b = 14, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::1. a=10,b=14,c

  播放段落

  2.  $\begin{align*}a = 6, b = \underline{\;\;\;\;\;\;\;}, c = 10\end{align*}$
  ::2. a=6,bc=10

  播放段落

  3.  $\begin{align*}a = \underline{\;\;\;\;\;\;\;}, b = 12, c =15\end{align*}$
  ::3. a*,b=12,c=15

  播放段落

  4.  $\begin{align*}a = 15, b = \underline{\;\;\;\;\;\;\;}, c = 25\end{align*}$
  ::4. a=15,bc=25

  播放段落

  5.  $\begin{align*}a = \underline{\;\;\;\;\;\;\;}, b = 32, c = 40\end{align*}$
  ::5. a,b=32,c=40

  播放段落

  6.  $\begin{align*}a = 30, b = 40, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::6. a=30,b=40,c=______________________________________________________________________________________________________________________________________________________________________

  播放段落

  7.  $\begin{align*}a = 1.5, b = 2, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::7. a=1.5,b=2,c

  播放段落

  8.  $\begin{align*}a = 4.5, b = 6, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::8. a=4.5,b=6,c

  播放段落

  9.  $\begin{align*}a = 6.6, b = 8.8, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::9. a=6.6,b=8.8,c

  播放段落

  10.  $\begin{align*}a = 36, b = 48, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::10=36,b=48,c

  播放段落

  11.  $\begin{align*}a = 27, b = 36, c = \underline{\;\;\;\;\;\;\;}\end{align*}$
  ::11=27,b=36,c

  播放段落

  Answer each question.
  ::回答每个问题。

  播放段落

  12. A television is measured by the length of the diagonal from one corner to another. If the screen is 8 inches by 15 inches, what is the length of the diagonal?
  ::12. 电视用从一个角落到另一个角落的对角长度来衡量,如果屏幕是8英寸乘15英寸,那么对角长度是多少?

  播放段落

  13. Do the numbers 15, 20 and 25 comprise a Pythagorean Triple?
  ::13. 数字15、20和25是否构成毕达哥伦三重赛?

  播放段落

  14. What is the perimeter of a right triangle with a hypotenuse of 30 inches and a leg of 18 inches?
  ::14. 右三角形的周界是什么? 右三角形的下限为30英寸,右三角形的腿为18英寸。

  播放段落

  15. What is the area of a right triangle with a hypotenuse of 30 inches and a leg of 18 inches?
  ::15. 右三角形的下限为30英寸、腿为18英寸的面积是多少?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。