Course: 7.10 确定和使用远距离公式

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 确定和使用远程公式

Collapse Expand
确定和使用远程公式
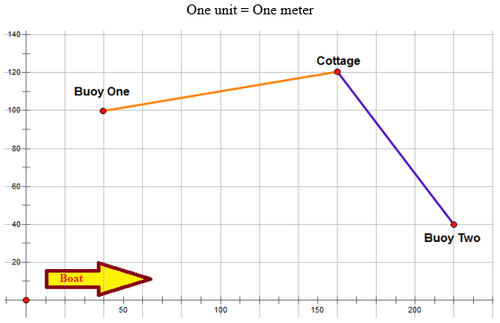
As Ross was cruising on his boat toward the cottage, he was concentrating on finding a new mooring for his boat. He had previously sunk two buoy markers in the water near the cottage and both locations had ample water below for the boat. Ross looked at his chart plot which showed the coordinates for the cottage and the two buoys. He decided to choose the buoy closest to the cottage.
::当罗斯在前往小屋的船上巡航时,他正集中精力寻找一条新的船锚,他以前曾在小屋附近的水中沉没了两个浮标标记,两个地点都为小屋提供了充足的水。罗斯查看了他的图表图图,其中显示了小屋和两个浮标的坐标。他决定选择离小屋最近的浮标。

How can Ross use the coordinates from the chart plot to figure out which buoy is closest to the cottage?
::罗斯如何使用图表图上的坐标找出哪个浮标离小屋最近?

In this concept, you will learn to identify and use the distance formula.
::在此概念中,您将学会识别和使用距离公式。

Distance Formula
::距离公式

When plotting points or graphing lines on a Cartesian grid, the coordinates of the points, or of the endpoints, of the graphed line are very useful when solving real-world problems.
::当在笛卡尔网格上绘制点或绘图线时,图形化线的点或终点的坐标对于解决现实世界的问题非常有用。

The following graph shows an orange line that represents the distance between the pet store (1, 6) and the drug store (8, 2). The green dot on the grid represents Timothy who is sitting on a bench in the Mall. To his right he can see the drug store and straight ahead he can see the pet store. He decides the pet store is closer so he goes there first. He exits the pet store and tries to decide whether to go back to the bench and then to the drug store or to walk diagonally to the drug store. Which way would be the shorter of the two distances if each side of the squares represents one yard?
::下图显示了一条橙色线,它代表宠物商店(1、6)和药店(8、2)之间的距离。网格上的绿点代表坐在购物中心长凳上的Timothy。在他右侧,他可以看到药店,直直前看宠物商店。他决定宠物商店更近,因此他先到那里去。他走出宠物商店,试图决定是回到长椅,然后回到药店,还是直行到药店。如果广场的两侧代表一个院子,那么这条路会更短。

On the grid, draw a horizontal line from Timothy on the bench to the drug store. The length of this line can be found by counting the tops of the squares that the line passes through. The length of the line is 7 yards. Now, draw a vertical line from Timothy on the bench to the pet store. The length of this line can be found by counting the sides of the squares that the line passes through. The length of this line is 4 yards. The three lines form a right triangle and the Pythagorean Theorem can be used to find the diagonal distance between the pet store and the drug store. This diagonal distance is in fact the hypotenuse of the right triangle.
::在网格上, 从长椅上的Timothy 画一条水平线到药店。这条线的长度可以通过计数该行经过的方形的顶部来找到。线的长度是7码。现在, 从长椅上的Timothy画一条垂直线到宠物店。这条线的长度可以通过计数该行经过的方形的两侧来找到。这个线的长度是4码。这条线的长度是4码。 3条线形成一个右三角形和Pythagorean Theorem可以用来找到宠物店和药店之间的对角距离。这个对角距离事实上是右三角形的低位。

First, write the Pythagorean Theorem.
::首先,写下毕达哥里安神话

$\begin{aligned} c^{2} = a^{2} + b^{2} \end{aligned}$
$\begin{align*}c^2 = a^2 + b^2\end{align*}$
::c2=a2+b2 (千兆赫)

Next, determine the values of $\begin{align*}(a, b, c)\end{align*}$ for the Pythagorean Theorem.
::下一步,为毕达哥里安神话确定(a、b、c)值。

$\begin{aligned} \begin{array}{rcl} a & = & 4 \\ b & = & 7 \\ c & = & ? \end{array} \end{aligned}$
$\begin{align*}\begin{array} {rcl} a &=& 4 \\ b &=& 7 \\ c &=& ? \end{array}\end{align*}$
::a=4b=7c=4b=7c=?

Next, fill these values into the Pythagorean Theorem.
::接下来,将这些值填入毕达哥里安理论。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ c^{2} & = & (4)^{2} + (7)^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2 \\ c^2 &=& (4)^2 + (7)^2 \end{array}\end{align*}$
::c2=a2+b2c2=(4)2+(7)2

Next, perform the indicated squaring on the right side of the equation and simplify.
::下一步,在方程右侧进行标明的对角并简化。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & (4)^{2} + (7)^{2} \\ c^{2} & = & (4 \times 4) + (7 \times 7) \\ c^{2} & = & 16 + 49 \\ c^{2} & = & 65 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& (4)^2 + (7)^2 \\ c^2 &=& (4 \times 4) + (7 \times 7) \\ c^2 &=& 16 + 49 \\ c^2 &=& 65 \end{array}\end{align*}$
::c2=(4)2+(7)2c2=(4×4)+(7×7)c2=16+49c2=65

Then, solve for the variable ‘ $\begin{align*}c\end{align*}$ ’ by taking the square root of both sides of the equation.
::然后,用方程式两侧的平方根解决变量“c”。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & 65 \\ \sqrt{c^{2}} & = & \sqrt{65} \\ c & = & 8.06 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& 65 \\ \sqrt{c^2} &=& \sqrt{65} \\ c &=& 8.06 \end{array}\end{align*}$
::c2=65c2=65c=8.06

The answer is 8.06.
::答案是8.06。

The diagonal distance between the pet store and the drug store is 8.06 yards.
::宠物店和药店之间的对角距离是8.06码

It would be a shorter distance for Timothy to walk than to return the 4 yards to the bench and then walk another 7 yards to the drug store.
::Timothy走路的距离要短一些比把4码的船送回长椅上然后再再走7码到药店要短一些

This method of finding the distance between two points requires that the diagram be drawn on grid paper which may be neither available nor convenient. Another way of finding the distance between two points with known coordinates is to use the distance formula. The distance formula is the square root of the square of the difference between the $\begin{align*}x\end{align*}$ -coordinates of the two points plus the square of the difference between the $\begin{align*}y\end{align*}$ -coordinates of the two points. The distance formula is written as:
::找到两个点之间的距离的方法要求图表在网格纸上绘制,而这种网格纸可能既不可用,也不方便。找到两个点之间有已知坐标的距离的另一个方法是使用距离公式。距离公式是两个点的X坐标之间的正方形根,加上两个点的Y坐标之间的正方形。距离公式的写法是:

$\begin{aligned} d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{aligned}$
$\begin{align*}d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\end{align*}$
::d=(x2-x1)2+(y2-y1)2

such that $\begin{align*}(x_1, y_1)\end{align*}$ are $\begin{align*}(x_2, y_2)\end{align*}$ the coordinates of the point chosen as the first point and the point chosen as the second point respectively. Once the points have been designated, the corresponding values must remain consistent and be substituted into the formula as named.
::例如 (x1,y1) 是(x2,y2) 选定的第一个点的坐标, 和选择的第二个点的坐标。一旦指定了点, 相应的值必须保持一致, 并替换为指定的公式。

Let’s apply this formula to find the distance between the pet store and the drug store. Remember the coordinates of the pet store were (1, 6) and those of the drug store were (8, 2).
::让我们应用这个公式来寻找宠物商店和药店之间的距离。记住宠物商店的座标是(1, 6),药店的座标是( 8, 2) 。

First, choose the first and second points. The answer will be the same regardless of how the points are chosen. Naming the points as shown below will help match the correct value with its corresponding variable.
::首先,选择第一点和第二点。答案将是相同的,无论选择的点是如何选择的。下面列出的点名将有助于将正确值与其相应的变量匹配。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 1, & 6 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 8, & 2 \end{matrix}) \end{aligned}$
$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 1, & 6 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2, & y_2 \\ 8, & 2 \end{pmatrix}\end{align*}$
:x1,y11,6)和(x2,y28,2)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(8 - 1)^{2} + (2 - 6)^{2}} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ d &=& \sqrt{(8-1)^2 + (2-6)^2} \end{array}\end{align*}$
::d=(x2-x1)2+(y2-y1)2+(y2-y1)2d=(8-1)2+(2-6)2

Next, perform the operations shown under the square root sign.
::下一步,执行在平方根符号下显示的操作。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(8 - 1)^{2} + (2 - 6)^{2}} \\ d & = & \sqrt{(7)^{2} + (- 4)^{2}} \\ d & = & \sqrt{(7 \times 7) + (- 4 \times - 4)} \\ d & = & \sqrt{49 + 16} \\ d & = & \sqrt{65} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(8-1)^2 + (2-6)^2} \\ d &=& \sqrt{(7)^2+ (-4)^2} \\ d &=& \sqrt{(7 \times 7) + (-4 \times -4)} \\ d &=& \sqrt{49 + 16} \\ d &=& \sqrt{65} \end{array}\end{align*}$
::d=8-1 2+(2-6)2d=(7)2+(-4)2d=(7×7)+(-4)4d=(-4)4d=49+16d=65)

Then, take the square root of 65 and round the answer to the nearest hundredth.
::然后,把65的平方根并绕过答案到最近的一百。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{65} \\ d & = & 8.06 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{65} \\ d &=& 8.06 \end{array}\end{align*}$
::d=65d=8.06

The answer is 8.06
::答案是8.06

The distance is 8.06 yards.
::距离是8.06码

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Ross and the two buoys. He needs to figure out which buoy is closer to the cottage, so he can moor his boat. Ross needs to use the distance formula to figure out which buoy is closer to the cottage.
::早些时候,你遇到了关于罗斯和两个浮标的问题。他需要弄清楚哪个浮标离小屋更近,以便他能够停泊船。罗斯需要用距离公式来弄清楚哪个浮标离小屋更近。

First, write the coordinates for each distance to be calculated and use the distance formula to calculate each distance to the nearest hundredth.
::首先,写出计算每一距离的坐标,并使用距离公式计算距离最近的一百度。

$\begin{aligned} \begin{array}{rcl} Cottage to Buoy One & Cottage to Buoy Two \\ (160, 120) and (40, 100) & (160, 120) and (220, 40) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \text{Cottage to Buoy One} & \quad & \text{Cottage to Buoy Two} \\ (160, 120) \ \text{and} \ (40, 100) & \quad & (160, 120) \ \text{and} \ (220, 40) \end{array}\end{align*}$
::Buy OneCottage to Buoy Two(160,120)和(40,100(160,120)和(220,40))

Distance from cottage to Buoy One:
::从小屋到 Buy One 的距离:

First, name the first and second points.
::首先,列出第一点和第二点。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 160, & 120 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 40, & 100 \end{matrix}) \end{aligned}$
$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 160, & 120 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2, & y_2 \\ 40, & 100 \end{pmatrix}\end{align*}$
:x 1,911,120美元)和(x2,y240,100美元)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(40 - 160)^{2} + (100 - 120)^{2}} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ d &=& \sqrt{(40 - 160)^2 + (100 - 120)^2} \end{array}\end{align*}$
::d=(x2-x1)2+(y2-y1)2+(y2-y1)2d=(40-160)2+(100-120)2

Next, perform the operations shown under the square root sign.
::下一步,执行在平方根符号下显示的操作。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(40 - 160)^{2} + (100 - 120)^{2}} \\ d & = & \sqrt{(- 120)^{2} + (- 20)^{2}} \\ d & = & \sqrt{(- 120 \times - 120) + (- 20 \times - 20)} \\ d & = & \sqrt{14400 + 400} \\ d & = & \sqrt{14800} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(40 - 160)^2 + (100 - 120)^2} \\ d &=& \sqrt{(-120)^2 + (-20)^2} \\ d &=& \sqrt{(-120 \times -120) + (-20 \times -20)} \\ d &=& \sqrt{14400 + 400} \\ d &=& \sqrt{14800} \end{array}\end{align*}$
::d=(40-160)2+(100-120)2d=(120)2+(20)2d=(120)2+(20)2d=(120)120+(20)120)+(20)+(20)20)d=14400+400d=14800

Then, take the square root of 14800 and round the answer to the nearest hundredth.
::然后,以14800的平方根并绕过答案到最近的一百。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{14800} \\ d & = & 121.66 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{14800} \\ d &=& 121.66 \end{array}\end{align*}$
::d=14800d=121.66

The answer is 121.66.
::答案是121.66。

The distance from the cottage to Buoy One is 121.66 meters.
::从小屋到Buoy One的距离是121.66米

Distance from cottage to Buoy Two:
::从小屋到布瓦二号的距离:

First, name the first and second points.
::首先,列出第一点和第二点。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 160, & 120 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 220, & 40 \end{matrix}) \end{aligned}$
$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 160, & 120 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2, & y_2 \\ 220, & 40 \end{pmatrix}\end{align*}$
:x 1,y1160,120)和(x2,y2220,40)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(220 - 160)^{2} + (40 - 120)^{2}} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ d &=& \sqrt{(220 - 160)^2 + (40 - 120)^2} \end{array}\end{align*}$
::d=(x2-x1)2+(y2-y1)2+(y2-y1)2d=(220-160)2+(40-120)2

Next, perform the operations shown under the square root sign.
::下一步,执行在平方根符号下显示的操作。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(220 - 160)^{2} + (40 - 120)^{2}} \\ d & = & \sqrt{(60)^{2} + (- 80)^{2}} \\ d & = & \sqrt{(60 \times 60) + (- 80 \times - 80)} \\ d & = & \sqrt{3600 + 6400} \\ d & = & \sqrt{10000} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(220 - 160)^2 + (40 - 120)^2} \\ d &=& \sqrt{(60)^2 + (-80)^2} \\ d &=& \sqrt{(60 \times 60) + (-80 \times -80)} \\ d &=& \sqrt{3600 + 6400} \\ d &=& \sqrt{10000} \end{array}\end{align*}$
::d=(220-160)2+(40-120)2d=(602+(-80)2d=(60x60)60+(-80)60+(-80)_80)d=3600+6400d=1000

Then, take the square root of 10000 and round the answer to the nearest hundredth.
::然后把10000的平方根绕到最近的第一百个答案

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{10000} \\ d & = & 100 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{10000} \\ d &=& 100 \end{array}\end{align*}$
::d=1000d=100 =100

The answer is 100.
::答案是100

The distance from the cottage to Buoy Two is 100 meters. Ross will moor the boat at Buoy Two.
::从小屋到布伊二号的距离是100米罗斯会把船停在布伊二号

Example 2
::例2

Use the distance formula to find the distance between these points to the nearest tenth
::使用距离公式查找这些点与最接近 10 点之间的距离

$\begin{align*}A (54, 120)\end{align*}$ and $\begin{align*}B (113, 215)\end{align*}$
::A(54,120)和B(113,215)

First, name the first and second points.
::首先,列出第一点和第二点。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 54, & 120 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 113, & 215 \end{matrix}) \end{aligned}$
$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 54, & 120 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2, & y_2 \\ 113, & 215 \end{pmatrix}\end{align*}$
:x1,y154,120)和(x2,y2113,215)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(113 - 54)^{2} + (215 - 120)^{2}} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ d &=& \sqrt{(113 - 54)^2 + (215 - 120)^2} \end{array}\end{align*}$
::d=(x2-x1)2+(y2-y1)2d=(113-54)2+(215-120)2

Next, perform the operations shown under the square root sign.
::下一步,执行在平方根符号下显示的操作。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(113 - 54)^{2} + (215 - 120)^{2}} \\ d & = & \sqrt{(59)^{2} + (95)^{2}} \\ d & = & \sqrt{(59 \times 59) + (95 \times 95)} \\ d & = & \sqrt{3481 + 9025} \\ d & = & \sqrt{12506} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(113 - 54)^2 + (215 - 120)^2} \\ d &=& \sqrt{(59)^2 + (95)^2} \\ d &=& \sqrt{(59 \times 59) + (95 \times 95)} \\ d &=& \sqrt{3481 + 9025} \\ d &=& \sqrt{12506} \end{array}\end{align*}$
::d=(113-54)2+(215-1120)2d=(592+(952d=(59x59)+(952d=(59x59)+(95x95)5d=3481+9025d=12506)

Then, take the square root of 12506 and round the answer to the nearest tenth.
::然后把12506的平方根绕到最近的第十根

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{12506} \\ d & = & 111.8 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{12506} \\ d &=& 111.8 \end{array}\end{align*}$
::d=12506d=111.8

The answer is 111.8 units.
::答案是111.8个单位。

Example 3
::例3

Use the distance formula to find the distance between the points $\begin{align*}D (3, -4)\end{align*}$ and $\begin{align*}E (-2, -10)\end{align*}$ .
::使用距离公式查找点D(3)至(4)与点E(-2)至点E(2)至(10)之间的距离。

First, name the first and second points.
::首先,列出第一点和第二点。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 3, & - 4 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ - 2, & - 10 \end{matrix}) \end{aligned}$
$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 3, & -4 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2 ,& y_2 \\ -2, & -10 \end{pmatrix}\end{align*}$
:x1,y13,-4)和(x2,y2-2,-2,-10)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(- 2 - 3)^{2} + (- 10 - (- 4))^{2}} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ d &=& \sqrt{(-2 -3)^2 + (-10 - (-4))^2} \end{array}\end{align*}$
::d=(x2-x1)2+(y2-y1)2d=(-2-3)2+(-10-(-4))2

Next, perform the operations shown under the square root sign.
::下一步,执行在平方根符号下显示的操作。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(- 2 - 3)^{2} + (- 10 - (- 4))^{2}} \\ d & = & \sqrt{(- 5)^{2} + (- 6)^{2}} \\ d & = & \sqrt{(- 5 \times - 5) + (- 6 \times - 6)} \\ d & = & \sqrt{25 + 36} \\ d & = & \sqrt{61} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(-2 -3)^2 + (-10 - (-4))^2} \\ d &=& \sqrt{(-5)^2 + (-6)^2} \\ d &=& \sqrt{(-5 \times -5) + (-6 \times -6)} \\ d &=& \sqrt{25+36} \\ d &=& \sqrt{61} \\ \end{array}\end{align*}$
::d=(-2-3)2+(-10-(-4))2d=(-5)2+(-6)2d=(-5)2+(-6)2d=(-5)5)+(-6)6d=25+36d=61

Then, take the square root of 61 and round the answer to the nearest tenth.
::然后,以61的平方根并绕过答案到最近的十分之一。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{61} \\ d & = & 7.8 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{61} \\ d &=& 7.8 \end{array}\end{align*}$
::d=61d=7.8 d=61d=7.8

The answer is 7.8.
::答案是7.8

The distance from $\begin{align*}D\end{align*}$ to $\begin{align*}E\end{align*}$ is 7.8 units.
::从D到E的距离是7.8个单位。

Example 4
::例4

The following circle has its center at the point (5, 3) and a radius of 3 inches. Use the distance formula to determine if the point (8, 5) is inside the circle, on the circle or outside the circle.
::以下圆的中点为5、3和半径为3英寸。使用距离公式确定点(8、5)是否在圆内、圆上或圆外。

You must use the distance formula to find the distance between the center of the circle (5, 3) and the point (8, 5).
::您必须使用距离公式来查找圆的中心( 5, 3) 和点( 8, 5) 之间的距离。

First, name the first and second points.
::首先,列出第一点和第二点。

$\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 5, & 3 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 8, & 5 \end{matrix}) \end{aligned}$
$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 5, & 3 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2, & y_2 \\ 8, & 5 \end{pmatrix}\end{align*}$
:x1,y15,3)和(x2,y28,5)

Next, write the distance formula and fill in the values for the variables.
::下一步,写入距离公式,填入变量的值。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \\ d & = & \sqrt{(8 - 5)^{2} + (5 - 3)^{2}} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ d &=& \sqrt{(8-5)^2 + (5-3)^2} \end{array}\end{align*}$
::d=(x2-x1)2+(y2-y1)2d=(8-5)2+(5-3)2

Next, perform the operations shown under the square root sign.
::下一步,执行在平方根符号下显示的操作。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{(8 - 5)^{2} + (5 - 3)^{2}} \\ d & = & \sqrt{(3)^{2} + (2)^{2}} \\ d & = & \sqrt{(3 \times 3) + (2 \times 2)} \\ d & = & \sqrt{9 + 4} \\ d & = & \sqrt{13} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{(8-5)^2 + (5-3)^2} \\ d &=& \sqrt{(3)^2 + (2)^2} \\ d &=& \sqrt{(3 \times 3) + (2 \times 2)} \\ d &=& \sqrt{9+4} \\ d &=& \sqrt{13} \end{array}\end{align*}$
::d=(8-5)2+(5-3)2d=(3)2+(2)2d=(3x3)+(2x2)d=9+4d=13

Then, take the square root of 13 and round the answer to the nearest tenth.
::然后,以13的平方根并绕过答案到最近的10。

$\begin{aligned} \begin{array}{rcl} d & = & \sqrt{13} \\ d & = & 3.6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& \sqrt{13} \\ d &=& 3.6 \end{array}\end{align*}$
::d=13d=3.6 d=13d=3.6

The answer is 3.6.
::答案是3.6。

The distance from the center of the circle to the point (8, 5) is 3.6 inches. The point will be outside the circle since this distance is greater than the length of the radius.Follow Up
::从圆的中心到点(8,5)的距离是3.6英寸。点在圆外,因为距离大于半径长度。

Review
::回顾

Use the distance formula to find the distance between the following pairs of points. You may round to the nearest tenth when necessary.
::使用距离公式查找以下两对点之间的距离。必要时您可以圆到最近的十分。

1. What is the distance between (3, 6) and (-1, 3)?
::1. (3,6)和(-1,3)之间的距离是多少?

2. What is the distance between (-2,-2) and (10, 3)?
::2. (2-2)和(10,3)之间的距离是多少?

3. What is the distance between (1,9) and (9,1)?
::3. (1,9)和(9,1)之间的距离是多少?

4. What is the distance between (-5,-5) and (-2,-1)?
::4. (5-5)和(2-1)之间的距离是多少?

5. What is the distance between (2, 12) and (3,7)?
::5. (2,12)和(3,7)之间的距离是多少?

6. What is the distance between (2, 2) and (8, 2)?
::6. (2,2)和(8,2)之间的距离是多少?

7. What is the distance between (-3, 4) and (2, 0)?
::7. (3、4)和(2,0)之间的距离是多少?

8. What is the distance between (3, 4) and (3, -4)?
::8. (3,4)和(3,4)之间的距离是多少?

9. What is the distance between (-4, -3) and (1, -1)?
::9. (4-4-3)和(1,-1)之间的距离是多少?

10. What is the distance between (-6, 2) and (-3, 1)?
::10. (-6,2)和(-3,1)之间的距离是多少?

Answer each of the following questions using the map below of Bryan’s town. Round to the nearest tenths place where needed.
::使用布赖恩镇下方的地图回答下列问题中的每一个问题。

11. The map below shows Bryan’s town. What is the distance between the pet store and town hall?
::11. 下面的地图显示了布赖恩的城镇,宠物商店和市政厅之间的距离是多少?

12. The map above shows Bryan’s town. What is the distance between the pet store and the courthouse?
::12. 上面的地图显示了布赖恩的城镇,宠物店和法院之间的距离是多少?

13. The map above shows Bryan’s town. What is the distance between the courthouse and the library?
::13. 上面的地图显示了布赖恩的城镇,法院与图书馆之间的距离是多少?

14. The map above shows Bryan’s town. What is the distance between the library and the town hall?
::14. 上面的地图显示了布赖恩的城镇,图书馆和市政厅之间的距离是多少?

15. The map above shows Bryan’s town. What is the distance between the pet store and the library?
::15. 上面的地图显示了布赖恩的城镇,宠物商店和图书馆之间的距离是多少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

General

确定和使用远程公式

Distance Formula ::距离公式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Distance Formula
::距离公式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源