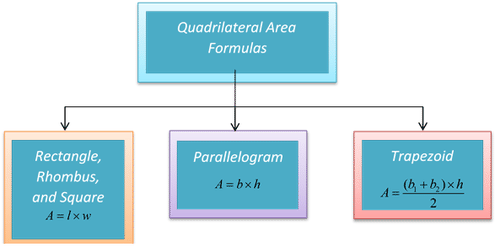
8.2 找出四方的方方面面和领域
章节大纲
-
Montgomery Middle School is going to host a school wide Olympics for the first time. The initial preparations have already started and a fantastic two day Olympic event will take place in six weeks. Mrs. Meery’s class will be building the platform for the award’s ceremony. The platform is in the shape of a trapezoid with bases 35 feet and 41 feet and a height of 7.5 feet. If one bucket of cement covers 25 square feet, how many buckets will the students need to build the platform?
::蒙哥马利中学将首次主办一场全学校奥林匹克运动会。 最初的准备工作已经开始,2天的奥运活动将在6周内举行。 Meery夫人的班级将为颁奖仪式建造平台。 平台的形状是35英尺、41英尺和7.5英尺高的陷阱。 如果一桶水泥覆盖25平方英尺,学生们需要多少桶才能建造平台?In this concept, you will learn to find the dimensions and areas of different quadrilaterals.
::在这个概念中,你们将学会找到不同四边形的维度和领域。Quadrilaterals
::四方Quadrilaterals are four-sided polygons. They are classified by the characteristics of their sides and angles . , squares, , rhombi , and are all quadrilaterals. The images below show some of the quadrilaterals and their characteristics.
::四边形是四面多边形。它们按其侧面和角度的特性分类。 、 方形、 、 rhombi, 并且都是四边形。 下面的图像显示了一些四边形及其特性 。Each of these quadrilaterals has its own area formula.
::每个四边形都有自己的区域公式。Let’s look at an example.
::让我们举个例子。What is the area of a rectangle with a length of 6 inches and a width of 4 inches?
::长6英寸宽4英寸的矩形区域是什么?First, fill in what you know into the formula for the area of a rectangle.
::首先,填入您所知道的, 填入矩形区域的公式 。
::A=lxwA=6x4 A=lxwA=6x4Next, solve for .
::下一个是A
::A=6x4A=24The answer is 24.
::答案是24个。The area of the rectangle is , or 24 square inches.
::矩形区域为24英寸2或24平方英寸。Let’s look at another example.
::让我们再看看另一个例子。What is the area of the parallelogram below?
::下面的平行图是什么区域?First, substitute what you know into the formula for the .
::首先,将你所知道的 替换为公式。
::A=bxhA=4x5 =bxhA=4x5 =bxhA=4x5Next, solve for .
::下一个是A
::A=4×5A=20 A=4×5A=20The answer is 20.
::答案是20岁The area of the parallelogram is , or 20 square meters.
::平行图的面积为20平方米或20平方米。Let’s look at one more example.
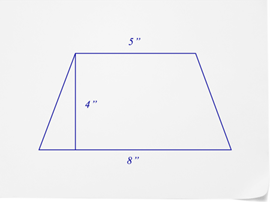
::让我们再举一个例子。Find the area of the trapezoid below.
::找到下面的捕捉细胞的区域First, substitute what you know into the formula for the area of a trapezoid.
::首先,将您所知道的替换成公式, 以取代树区域 。
::A=(b1+b2)xxh2A=(5+8)x42Next, solve for .
::下一个是A
::A=5+8)x42A=26The answer is 26.
::答案是26岁The area of the trapezoid is , or 26 square inches.
::类区域为26英寸2或26平方英寸。Examples
::实例Example 1
::例1Earlier, you were given a problem about the school’s podium.
::更早之前,The podium is in the shape of a trapezoid that has base measures of 35 feet and 41 feet and a height of 7.5 feet. The podium is being made of cement where one bucket of cement covers 25 square feet. You need to find the area of the podium and then the number of buckets of cement to make it.
::讲台的形状是角形,基度为35英尺,41英尺,高7.5英尺;讲台是用水泥制成的,一桶水泥覆盖25平方英尺;你需要找到讲台的面积,然后是水泥桶的数量。First, substitute what you know into the formula for the area of a trapezoid.
::首先,将您所知道的替换成公式, 以取代树区域 。
::A=(b1+b2)xxh2A=(35+41)x7.52Next, solve for .
::下一个是A
::A=35+41x7.52A=285Then, divide the area by 25 in order to determine the number of buckets of cement to use.
::然后,将面积除以25,以确定需要使用的水泥桶数量。
::桶 # = 28525 # 桶 # 11.4The answer is 11.4.
::答案是11.4。The students will have to buy 12 buckets of cement for their project.
::学生必须购买12桶水泥,Example 2
::例2A parallelogram has an area of . The height of the parallelogram is . What is its base?
::平行图的面积为105平方米,平行图的高度为7米。其基数是多少?First, substitute what you know into the formula for the area of a parallelogram.
::首先,将您所知道的替换成公式, 以取代平行图区域 。
::A=bxh105=bx7Next, divide both sides by 7 to solve for .
::接下来,将双方除以7,解决b。
::105=b×71057=7b7b=15The answer is 15.
::答案是15岁The base of the parallelogram has a length of .
::平行图的底部长度为15米。Example 3
::例3What is the area of a square with a side length of 4.5 inches?
::边长4.5英寸的方形面积是多少?First, substitute what you know into the formula for the area of a square.
::首先,将您所知道的替换成方形区域的公式。
::A=lxwA=4.5x4.5Next, solve for .
::下一个是A
::A=4.5x4.5A=20.25The answer is 20.25. Therefore the area of the square is , or 20.25 square inches.
::答案是20.25。因此,广场面积是20.25英寸,即20.25英寸。Example 4
::例4What is the area of a rectangle with a length of 8 feet and a width of 6.25 feet?
::长8英尺、宽6.25英尺的矩形区域是什么?First, substitute what you know into the formula for the area of a rectangle.
::首先,将您所知道的替换为矩形区域的公式。
::A=lxwA=8x6.25Next, solve for .
::下一个是A
::A=8x6.25A=50The answer is 50.
::答案是50The area of the rectangle is , or 50 square feet.
::矩形区域为50平方英尺或50平方英尺。Example 5
::例5What is the area of a parallelogram with a base of 10 meters and a height of 7.5 meters?
::以10米和7.5米为基数的平行图的面积是多少?First, substitute what you know into the formula for the area of a parallelogram.
::首先,将您所知道的替换成公式, 以取代平行图区域 。
::A=bxhA=10x7.5Next, solve for .
::下一个是A
::A=10x7.5A=75The answer is 75.
::答案是75The area of the parallelogram is , or 75 square meters.
::平行图的面积为75平方米,即75平方米。Review
::回顾1.
::1.l=10英寸,W=7.5英寸2.
::2. l=12英尺,w=9英尺3.
::3. 1=14英尺, w=11英尺4.
::4. I=21英尺,W=19英尺Find the area of each parallelogram.
::查找每个平行图的区域 。5.
::5. b=11英尺,h=9英尺6.
::6. b=13 英寸, h=11 英寸7.
::7. b=22英尺,h=19英尺8.
::8. b=31米,h=27米Find the area of each trapezoid.
::找到每个的面积。9.
::9. 基数=5和8英寸,高度=4英寸10.
::10. 基数=6和8英寸,高度=5英寸11.
::11. 基数=10英尺和12英尺,高度=9英尺Find the area of each square. Round your answer to the nearest hundredths place if needed.
::查找每个广场的面积。 如果需要, 将您的答复回合到最近的一百个位置 。12. side length of 8 inches
::12 侧长8 英寸13. side length of 15 feet
::13. 侧长15英尺14. side length of 22.5 mm
::12.5毫米14侧长22.5毫米15. side length of 18.25 cm
::15长18.25厘米半长Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。Resources
::资源