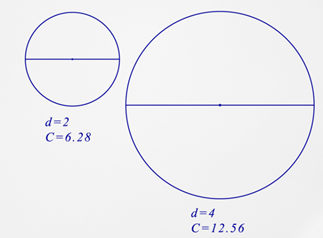Course: 8.3 圆环环环 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 圆环环环

Collapse Expand
圆环环环
Thomas is practicing throwing an old discus ring he found in the attic. After an exhausting afternoon, Thomas sits with the discus ring and starts to examine it. He uses a ruler to measure the radius , which is 11 cm. He also finds a way to measure the diameter of the circle he marked out to throw the discus into – it’s 2.5 m across. Now that he has this information about both circles, how can Thomas figure out the of each?
::Thomas正在练习扔一个他在阁楼里发现的旧迪斯环。过了一个精疲力尽的下午,Thomas就坐在迪斯环上开始检查它。他用一个尺子测量半径,即11厘米。他还找到了一种测量他所标定的圆圈直径的方法,将迪斯投进一个圆圈的直径 — — 跨度为2.5米。既然他掌握了关于两圈的信息,Thomas如何能找出每个圆圈的直径?

In this concept, you will learn to find the diameter, radius and circumference of circles.
::在这个概念中,你会学会找到圆的直径、半径和环形。

Circumference
::环环境

Circles are unique geometric figures. A circle is the set of points that are equidistant from a center point . The radius of a circle is the distance from the center to any point on the circle. The diameter is the distance across the circle through the center. The diameter is always twice as long as the radius.
::圆形是独特的几何数字。圆形是一组从中点到中点的等距点。圆圆半径是中点到圆角中任何点的距离。直径是圆圈穿过中点的距离。直径总是是半径的两倍。

You also use the special number pi $\begin{align*}(\pi)\end{align*}$ when dealing with circle calculations. Pi is a decimal that is infinitely long $\begin{align*}(3.14159265 \ldots)\end{align*}$ , but in your calculations you round it to 3.14. Pi is the ratio of the circumference, or distance around a circle, to the diameter.
::您在处理圆形计算时也使用特殊数字 pi 。 Pi 是一个无限长的十进制( 3. 14159265...) , 但在您计算时, 您将它绕到 3. 14 。 Pi 是圆周绕或圆圈距离与直径的比。

Circles are special in geometry because this ratio of the circumference and the diameter always stays the same. In other words, these two measurements are related. If you change the diameter, the circumference changes proportionally. For example, if you double the length of the diameter, the circumference doubles also.
::在几何学中,圆圈是特殊的,因为环形和直径的这个比例总是保持不变。换句话说,这两个测量是相互关联的。如果改变直径,则环形会成比例变化。例如,如果将直径的长度增加一倍,则环形也会翻倍。

Look at the circles below. Find the ratio of the circumference to the diameter for both circles. What do you notice?
::看看下面的圆圈。找到两圈的环形与直径之比。您注意到什么 ?

$\begin{aligned} \begin{array}{rcl} Large Circle \\ \frac{circumference}{diameter} = \frac{12.56}{4} \\ \frac{circumference}{diameter} = 3.14 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} && \qquad \quad \quad \text{Large Circle} \\ \\ && \quad \ \frac{\text{circumference}}{\text{diameter}} = \frac{12.56}{4} \\ && \quad \ \frac{\text{circumference}}{\text{diameter}} = 3.14 \end{array}\end{align*}$
::大型圆环环环形仪=12.564 环环形仪=3.14

$\begin{aligned} \begin{array}{rcl} Small Circle \\ \frac{circumference}{diameter} = \frac{6.28}{2} \\ \frac{circumference}{diameter} = 3.14 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} && \qquad \quad \quad \text{Small Circle} \\ \\ && \quad \ \frac{\text{circumference}}{\text{diameter}} = \frac{6.28}{2} \\ && \quad \ \frac{\text{circumference}}{\text{diameter}} = 3.14 \end{array}\end{align*}$
::小圆环环形仪=6.282 环形仪=3.14

Notice, when you divide the circumference of a circle by its diameter, no matter how big or small the circle is, you will always get the same number. Whenever you divide the circumference by the diameter, you will always get 3.14, pi .
::注意, 当您将圆的环形除以其直径时, 无论圆的大小大小, 您都会得到相同的数字。当您将环形除以直径时, 您就会得到3. 14, pi 。

The circumference of a circle can be found using the formula: $\begin{align*}C=\pi d\end{align*}$ . Since the diameter $\begin{align*}(d)\end{align*}$ is twice the radius $\begin{align*}(r)\end{align*}$ , you can also use the formula: $\begin{align*}C=2 \pi r\end{align*}$
::使用公式Cd。由于直径(d)是半径的两倍(r),您也可以使用公式:C=2r。

Let’s look at an example.
::让我们举个例子。

What is the circumference of a circle that has a diameter of 3 inches?
::一个直径为3英寸的圆圈的环形是什么?

First, substitute what you know into the formula for circumference.
::首先,用你所知道的代替环形的公式

$\begin{aligned} \begin{array}{rcl} C & = & π d \\ C & = & π \times 3 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi d \\ C &=& \pi \times 3 \end{array}\end{align*}$
::CdC 3号

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & π \times 3 \\ C & = & 9.42 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi \times 3 \\ C &=& 9.42 \end{array}\end{align*}$
::C3C=9.42

The answer is 9.42.
::答案是9.42。

The circumference is 9.42 inches.
::周长为9.42英寸

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Thomas and his discus.
::早些时候,你被托马斯和他的舞厅给惹了麻烦

The discus ring has a radius of 11 cm. The throwing area has a diameter of 2.5 m.
::圆盘环半径为11厘米。抛掷区直径为2.5米。

First, substitute what you know into the formula for circumference to find the circumference of the discus.
::首先,用你所知道的来取代环形的公式以找到光碟的环形

$\begin{aligned} \begin{array}{rcl} C & = & 2 π r \\ C & = & 2 π \times 11 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& 2 \pi r \\ C &=& 2 \pi \times 11 \end{array}\end{align*}$

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & 2 π \times 11 \\ C & = & 69.12 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& 2 \pi \times 11 \\ C &=& 69.12 \end{array} \end{align*}$

The answer is 69.12.
::答案是69.12。

The circumference of the discus is 69.1 cm.
::光谱环绕69.1厘米。

Then, substitute what you know into the formula for circumference to find the circumference of the discus throwing area.
::然后,用你所知道的代替环形的公式以找到圆盘投掷区的环形

$\begin{aligned} \begin{array}{rcl} C & = & π d \\ C & = & π \times 2.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi d \\ C &=& \pi \times 2.5 \end{array}\end{align*}$

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & π \times 2.5 \\ C & = & 7.85 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi \times 2.5 \\ C &=& 7.85 \end{array}\end{align*}$
::C2.5C=7.85

The answer is 7.85.
::答案是7.85。

The circumference of the throwing circle for the discus is 7.85 meters.
::圆盘环绕7.85米

Example 2
::例2

What is the circumference of a circle if the radius is 2.5 feet?
::如果半径为2.5英尺,圆圈的环形是什么?

First, substitute what you know into the formula for circumference.
::首先,用你所知道的代替环形的公式

$\begin{aligned} \begin{array}{rcl} C & = & 2 π r \\ C & = & 2 π \times 2.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& 2 \pi r \\ C &=& 2 \pi \times 2.5 \end{array}\end{align*}$
::C=2rC=22.5

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & 2 π \times 2.5 \\ C & = & 15.71 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& 2 \pi \times 2.5 \\ C &=& 15.71 \end{array}\end{align*}$
::C=22.5C=15.71

The answer is 15.71.
::答案是15.71。

The circumference is 15.7 feet.
::周长为15.7英尺

Example 3
::例3

Find the circumference of each circle given the diameter is 6 inches.
::根据直径为6英寸,找到每个圆圈的环形。

First, substitute what you know into the formula for circumference.
::首先,用你所知道的代替环形的公式

$\begin{aligned} \begin{array}{rcl} C & = & π d \\ C & = & π \times 6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi d \\ C &=& \pi \times 6 \end{array}\end{align*}$
::CdC6

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & π \times 6 \\ C & = & 18.85 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi \times 6 \\ C &=& 18.85 \end{array}\end{align*}$
::C6C=18.85

The answer is 18.85.
::答案是18.85块

The circumference is 18.85 inches.
::周长18.85英寸

Example 4
::例4

Find the circumference of each circle given the radius is 4.5 feet.
::如果半径为4.5英尺,则查找每个圆圈的环形。

First, substitute what you know into the formula for circumference.
::首先,用你所知道的代替环形的公式

$\begin{aligned} \begin{array}{rcl} C & = & 2 π r \\ C & = & 2 π \times 4.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& 2 \pi r \\ C &=& 2 \pi \times 4.5 \end{array} \end{align*}$
::C=2rC=24.5

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & 2 π \times 4.5 \\ C & = & 28.27 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& 2 \pi \times 4.5 \\ C &=& 28.27 \end{array}\end{align*}$
::C=24.5C=28.27

The answer is 28.27.
::答案是28.27。

The circumference is 28.27 feet.
::周长为28.27英尺

Example 5
::例5

Find the circumference of each circle given the diameter is 3.5 meters.
::鉴于直径为3.5米,找到每个圆圈的环形。

First, substitute what you know into the formula for circumference.
::首先,用你所知道的代替环形的公式

$\begin{aligned} \begin{array}{rcl} C & = & π d \\ C & = & π \times 3.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi d \\ C &=& \pi \times 3.5 \end{array}\end{align*}$
::CdC 3.5

Next, solve for the circumference.
::下一个,解决环绕。

$\begin{aligned} \begin{array}{rcl} C & = & π \times 3.5 \\ C & = & 11.0 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} C &=& \pi \times 3.5 \\ C &=& 11.0 \end{array} \end{align*}$
::C3.5C=11.0。

The answer is 11.0.
::答案是11.0。

The circumference is 11.0 meters.
::周长为11.0米

Review
::回顾

Find the circumference of each circle given the radius or diameter. Use 3.14 to approximate $\begin{align*}\pi.\end{align*}$
::根据半径或直径,查找每个圆圈的环形。使用3.14到约。

1. $\begin{align*}d = 10 \ in\end{align*}$
::1. d=10 英寸

2. $\begin{align*}d = 5 \ in\end{align*}$
::2. d=5 英寸

3. $\begin{align*}d = 7 \ ft\end{align*}$
::3. d=7吨

4. $\begin{align*}d = 12 \ mm\end{align*}$
::4. d=12毫米

5. $\begin{align*}d = 14 \ cm\end{align*}$
::5. d=14厘米

6. $\begin{align*}r = 4 \ in\end{align*}$
::6 r= 4 英寸

7. $\begin{align*}r = 6 \ \text{meters}\end{align*}$
::7 r=6米

8. $\begin{align*}r = 8 \ ft.\end{align*}$
::8 r=8英尺。

9. $\begin{align*}r = 11 \ in\end{align*}$
::9 r= 11 英寸

10. $\begin{align*}r = 15 \ cm\end{align*}$
::10 r= 15厘米

Find the diameter given each circumference. Use 3.14 to approximate $\begin{align*}\pi.\end{align*}$
::查找给定每个环形的直径。使用 3. 14 到约x 。

11. $\begin{align*}53.38 \ \text{inches}\end{align*}$
::11.53.38英寸

12. $\begin{align*}43.96 \ \text{feet}\end{align*}$
::12.96英尺 43.96英尺

13. $\begin{align*}56.52 \ \text{inches}\end{align*}$
::13.52英寸56.52英寸

14. $\begin{align*}65.94 \ \text{meters}\end{align*}$
::14.94米

15. $\begin{align*}48.67 \ \text{meters}\end{align*}$
::15.67米

16. $\begin{align*}37.68 \ \text{feet}\end{align*}$
::16.68英尺

17. $\begin{align*}78.5 \ \text{meters}\end{align*}$
::17.5米

18. $\begin{align*}100.48 \ cm\end{align*}$
::18.100.48厘米

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

圆环环环

Circumference ::环环境

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Circumference
::环环境

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)