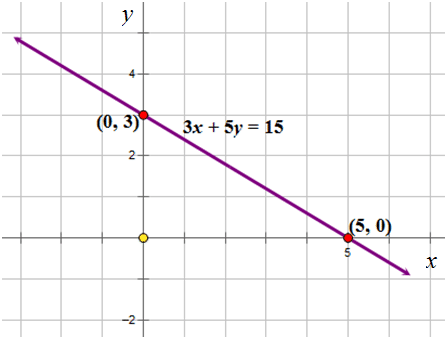Course: 9.10 绘图线性平方

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 直线方形

Collapse Expand
直线方形
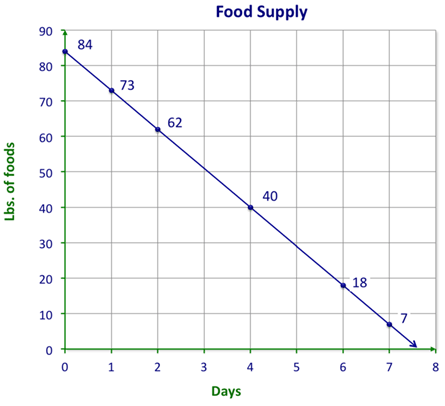
The local hiking club is finalizing its plans for a trip to the Rocky Mountains in Canada. The hikers are discussing the food they will have to carry with them to complete their climb up the mountains. The group decides to set out with 84 pounds of food and figures that, together, the hikers will eat 11 pounds each day. To make sure they will have enough food, the members of the club want to show how their food supply looks at the end of each day as well as at the end of their trip. What can the y do to create a visual picture of their food supply?
::当地登山俱乐部正在最后确定前往加拿大洛基山脉的行程计划。登山者们正在讨论他们必须随身携带的食品, 以完成登山。他们决定用84磅的食物和数字出发, 远山者们每天一起吃11磅。为了确保他们有足够的食物, 俱乐部成员想展示他们的食品供应在每天结束和旅程结束时的景象。他们能做些什么来制作他们的食品供应的视觉图片呢 ?

In this C oncept, you will learn to recognize functions
::在此概念中, 您将学会识别功能。

Graphing Linear Equations
::直线方形

When graphing a straight line, two points on the line must be plotted and joined. If an equation is written in standard form , the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ - intercepts can be calculated and plotted on the Cartesian grid. These plotted points can then be joined to graph the line represented by the equation.
::当绘制直线时, 线上的两个点必须绘制并合并。如果公式以标准格式写成, 则可以计算 X 和 y 界面, 并在笛卡尔网格上绘制。这些绘图点可以合并来绘制方程式所代表线的图形。

Let’s look at an example.
::让我们举个例子。

Plot the graph of the line represented by the following equation:
::绘制以下列方程式表示的线条图 :

$\begin{aligned} 3 x + 5 y = 15 \end{aligned}$
$\begin{align*}3x + 5y = 15\end{align*}$
::3x+5y=15

Look at the given equation. It is written in standard form.
::看看给定方程式,它以标准格式写成

$\begin{align*}Ax+By= C\end{align*}$ such that $\begin{align*}A=3, B=5,\end{align*}$ and $\begin{align*}C=15.\end{align*}$
::Ax+By=C,A=3,B=5,C=15。

First, calculate the $\begin{align*}x\end{align*}$ - intercept using the formula :
::首先,使用公式计算 x 界面 :

$\begin{aligned} x - intercept = \frac{C}{A} \end{aligned}$
$\begin{align*}x- \text{intercept} = \frac{C}{A}\end{align*}$
::x- 界面= CA

Next, fill in the values for $\begin{align*}C\end{align*}$ and $\begin{align*}A\end{align*}$ .
::接下来填入 C 和 A 的值。

$\begin{aligned} \begin{array}{rcl} x - intercept & = & \frac{C}{A} \\ x - intercept & = & \frac{15}{3} \\ x - intercept & = & 5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} x- \text{intercept} &=& \frac{C}{A}\\ x- \text{intercept} &=& \frac{15}{3}\\ x- \text{intercept} &=& 5 \end{array}\end{align*}$
::x- 截取= CAX- 截取= 153x- 截取= 5

The answer is 5.
::答案是5。

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(5,0)\end{align*}$ .
::x 拦截为 (5,0) 。

Second, calculate the $\begin{align*}y\end{align*}$ -intercept using the formula:
::第二,使用公式计算 Y 接口:

$\begin{aligned} y - intercept = \frac{C}{B} \end{aligned}$
$\begin{align*}y- \text{intercept} = \frac{C}{B}\end{align*}$
::y - 截取=CB

Next, fill in the values for $\begin{align*}C\end{align*}$ and $\begin{align*}B\end{align*}$ .
::下一步填入 C 和 B 的值。

$\begin{aligned} \begin{array}{rcl} y - intercept & = & \frac{C}{B} \\ y - intercept & = & \frac{15}{5} \\ y - intercept & = & 3 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y- \text{intercept} &=& \frac{C}{B} \\ y- \text{intercept} &=& \frac{15}{5} \\ y- \text{intercept} &=& 3 \end{array}\end{align*}$
::y- 截取= CBY- 截取= 155y- 截取= 3

The answer is 3.
::答案是3

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,3)\end{align*}$ .
::Y 界面是 (0, 3) 。

Next, plot the points $\begin{align*}(5,0)\end{align*}$ and $\begin{align*}(0,3)\end{align*}$ on the Cartesian grid and join them with a straight line.
::接下来,在笛卡尔语网格上绘制点数(5,0)和点数(0,3),并用直线连接它们。

However, the equation of a line is not always written in standard form. The equation of a straight line is often written in intercept form . Remember, the slope-intercept form of an equation is written as $\begin{align*}y=mx+b,\end{align*}$ such that ‘ $\begin{align*}m\end{align*}$ ’ is the slope of the line and ‘ $\begin{align*}b\end{align*}$ ’ is the $\begin{align*}y\end{align*}$ -intercept of the line. These two values can be used to plot two points on the Cartesian grid. Remember the value of the slope should be expressed in fraction form for graphing. The denominator of the fraction $\begin{align*} (m)\end{align*}$ is $\begin{align*}x_2 - x_1\end{align*}$ and should always be a positive value. A positive value means that the movement in a horizontal direction will always be to the right. The numerator of the fraction is $\begin{align*}y_2 -y_1\end{align*}$ and can be either a negative or a positive value.
::然而, 线条的方程式并不总是以标准形式写成。直线的方程式往往以截取的形式写成。记住, 方程式的斜度截取形式是y=mx+b, 也就是说, `m ' 是线的斜度, `b ' 是线的y- interitute。这两个值可用于在笛卡尔网格上绘制两点。记住, 斜度的值应该以小数形式表示, 以图解为单位。分数的分母( m) 是 x2 - x1, 并且应该始终是正值。积极的值意味着水平方向的移动总是向右, 分数的计算器是 y2-y1, 可以是负值或正值。

Let’s look at an example.
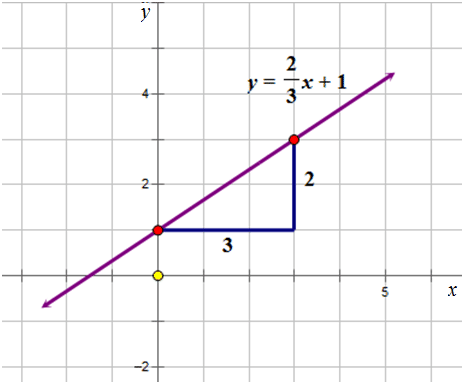
::让我们举个例子。

Plot the graph of the line represented by the following equation:
::绘制以下列方程式表示的线条图 :

$\begin{aligned} y = \frac{2}{3} x + 1 \end{aligned}$
$\begin{align*}y=\frac{2}{3}x+1\end{align*}$
::y=23x+1 y=23x+1

Look at the given equation. It is written in slope-intercept form.
::看看给定方程。它以斜坡界面的形式写成。

$\begin{align*}y=mx+b\end{align*}$ such that $\begin{align*}m=\frac{2}{3} \end{align*}$ and $\begin{align*}b=1\end{align*}$ or $\begin{align*}(0, 1).\end{align*}$
::y=mx+b, m=23和b=1或(0,1) 。

First, plot the $\begin{align*}y\end{align*}$ -intercept $\begin{align*}(b)\end{align*}$ on the Cartesian grid. From here, count to the right the number of units in the denominator of the slope fraction (3) and then up the number of units in the numerator of the slope fraction (2).
::首先, 在笛卡尔网格上绘制 Y 接口 (b) 。从这里, 向右计数斜度分数的分母中单位数量(3), 然后在斜度分数的分子中增加单位数量(2) 。

Then, join the two plotted points with a straight line.
::然后,你们用一条直线,和那两条划线的两条划线,一起划入其中。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about a hiking club and food. The hikers need to keep track of the 84 pounds of food they are carrying. If they eat 11 pounds of food a day, how can they create a visual display of the food they have left at the end of each day?
::早些时候,有人给了你一个关于远足俱乐部和食物的问题。远足者们需要追踪他们携带的84磅食物。如果他们每天吃11磅食物,他们怎么能够以视觉形式展示他们每天最后留下的食物?

First, write down the given information
::首先,写入给定信息

$\begin{align*}y=\end{align*}$ pounds of food left at the end of each day
::y = 每天结束时剩下的食物重量

$\begin{align*}m=\end{align*}$ pound of food eaten each day
::= 每天食用食物每磅

$\begin{align*}x=\end{align*}$ number of days hiking
::x=徒步旅行天数

$\begin{align*}b=\end{align*}$ number of pounds of food being carried
::b = 携带食物磅数

Next, substitute the known values into the equation.
::接下来,在方程中替换已知值。

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & - 11 d + 84 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx +b \\ y &=& \text{-}11d+84 \end{array}\end{align*}$
::y=mx+by=11d+84 y=mx+by=11d+84

Then, graph the equation on the Cartesian grid.
::然后在笛卡尔网格上绘制方程图

Example 2
::例2

Plot the graph of the following equation written in slope-intercept form.
::绘制下方程式的图形, 以斜坡界面的形式写成。

$\begin{aligned} y = - \frac{3}{4} x + 5 \end{aligned}$
$\begin{align*}y=\text{-}\frac{3}{4}x+5 \end{align*}$
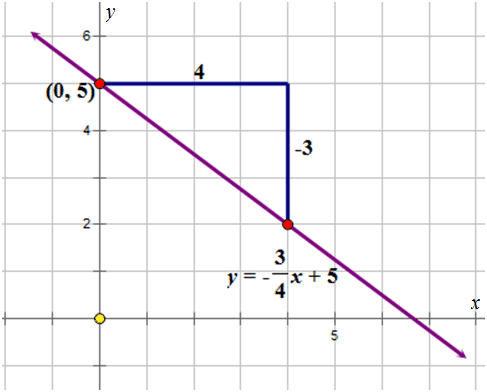
::y=-34x+5 y=-34x+5

First, write down the information given in the equation:
::首先,写下方程中给出的信息:

$\begin{align*}y=mx+b\end{align*}$ such that $\begin{align*}m=\text{-}\frac{3}{4}\end{align*}$ and $\begin{align*}b=5 : (0, 5).\end{align*}$
::y=mx+b, m=-34和b=50. 5)

Next, plot the $\begin{align*}y\end{align*}$ -intercept $\begin{align*}(0,5)\end{align*}$ on the Cartesian grid. From the $\begin{align*}y\end{align*}$ -intercept move to the right 4 units, move downward 3 units, and plot the point.
::接下来,在笛卡尔网格上绘制 Y 界面( 0, 5) 。从 y 界面移动到右侧 4 个单元, 向下移动 3 个单元, 并绘制点。

Then, join the two plotted points with a straight line.
::然后,你们用一条直线,和那两条划线的两条划线,一起划入其中。

Example 3
::例3

Plot the graph of the line represented by the following equation:
::绘制以下列方程式表示的线条图 :

$\begin{aligned} 4 x - 6 y = - 24 \end{aligned}$
$\begin{align*}4x-6y=\text{-}24\end{align*}$
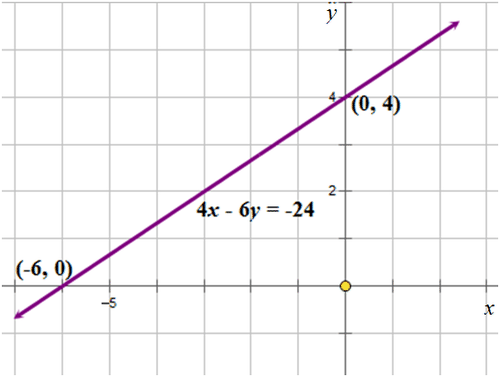
::4-6y=24

Look at the given equation. It is written in standard form.
::看看给定方程式,它以标准格式写成

$\begin{align*}Ax+By=C\end{align*}$ such that $\begin{align*}A=4, B=\text{-}6,\end{align*}$ and $\begin{align*}C=\text{-}24.\end{align*}$
::Ax+By=C,A=4,B=6,C=24。

First, calculate the $\begin{align*}x\end{align*}$ -intercept using the formula:
::首先,使用公式计算 x 界面 :

$\begin{aligned} x - intercept = \frac{C}{A} \end{aligned}$
$\begin{align*}x- \text{intercept} = \frac{C}{A}\end{align*}$
::x- 界面= CA

Next, fill in the values for $\begin{align*}C\end{align*}$ and $\begin{align*}A\end{align*}$ .
::接下来填入 C 和 A 的值。

$\begin{aligned} \begin{array}{rcl} x - intercept & = & \frac{C}{A} \\ x - intercept & = & \frac{- 24}{4} \\ x - intercept & = & - 6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} x- \text{intercept} &=& \frac{C}{A} \\ x- \text{intercept} &=& \frac{\text{-}24}{4} \\ x- \text{intercept} &=& \text{-}6 \end{array}\end{align*}$
::x- 截取= CAX- 截取=-244x- 截取=-6

The answer is -6.
::答案是 -6

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(\text{-}6,0)\end{align*}$ .
::X 拦截( 6, 0) 。

Second, calculate the $\begin{align*}y\end{align*}$ -intercept using the formula:
::第二,使用公式计算 Y 接口:

$\begin{aligned} y - intercept = \frac{C}{B} \end{aligned}$
$\begin{align*}y- \text{intercept} = \frac{C}{B}\end{align*}$
::y - 截取=CB

Next, fill in the values for $\begin{align*}C\end{align*}$ and $\begin{align*}B\end{align*}$ .
::下一步填入 C 和 B 的值。

$\begin{aligned} \begin{array}{rcl} y - intercept & = & \frac{C}{B} \\ y - intercept & = & \frac{- 24}{6} \\ y - intercept & = & 4 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y- \text{intercept} &=& \frac{C}{B} \\ y- \text{intercept} &=& \frac{\text{-}24}{6} \\ y- \text{intercept} &=& 4 \end{array}\end{align*}$ The answer is 4.
::y- 截取= CBY- 截取= 246y- 截取= 4 答案是 4 。

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,4)\end{align*}$ .
::Y 界面是 0, 4 。

Next, plot the points $\begin{align*}(\text{-}6,0)\end{align*}$ and $\begin{align*}(0,4)\end{align*}$ on the Cartesian grid and join them with a straight line.
::接下来,绘制笛卡尔网格上的点数(-6,0)和点数(0,4),并用一条直线连接它们。

Example 4
::例4

Plot the graph of the following equation written in slope-intercept form.
::绘制下方程式的图形, 以斜坡界面的形式写成。

$\begin{aligned} y = \frac{2}{5} x - 3 \end{aligned}$
$\begin{align*}y=\frac{2}{5}x-3\end{align*}$
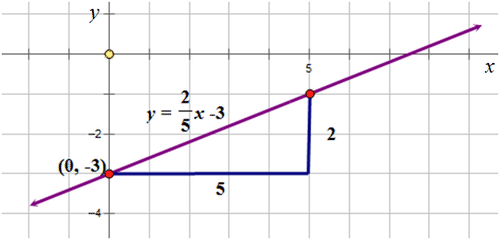
::y=25x-3

First, write down the information given in the equation:
::首先,写下方程中给出的信息:

$\begin{align*}y=mx+b\end{align*}$ such that $\begin{align*}m=\frac{2}{5}\end{align*}$ and $\begin{align*}b=\text{-}3 : (0,\text{-}3).\end{align*}$
::y=mx+b,m=25和b=30,3)。

Next, plot the $\begin{align*}y\end{align*}$ -intercept $\begin{align*}(0,-3)\end{align*}$ on the Cartesian grid. From the $\begin{align*}y\end{align*}$ -intercept move to the right 5 units, move upward 2 units, and plot the point.
::接下来,在笛卡尔网格上绘制 Y 界面( 0, 3) 。从 y 界面移动到右边 5 个单位, 向上移动 2 个单位, 并绘制点。

Then, join the two plotted points with a straight line.
::然后,你们用一条直线,和那两条划线的两条划线,一起划入其中。

Example 5
::例5

Rewrite the following equation written in standard form in slope-intercept form. State the slope and $\begin{align*}y\end{align*}$ -intercept of the line.
::以标准格式写成的以下方程式重写,以斜坡截面形式写成。标明线的斜坡和 Y 截面。

$\begin{aligned} 4 x - 5 y = 60 \end{aligned}$
$\begin{align*}4x-5y=60\end{align*}$
::4x-5y=60

First, subtract $\begin{align*}4x\end{align*}$ from both sides of the equation and simplify.
::首先,从方程两侧减去4x并简化。

$\begin{aligned} \begin{array}{rcl} 4 x - 5 y & = & 60 \\ 4 x - 4 x - 5 y & = & 60 - 4 x \\ - 5 y & = & 60 - 4 x \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 4x-5y &=& 60 \\ 4x-4x-5y &=& 60-4x \\ -5y &=& 60 - 4x \end{array}\end{align*}$
::4x-5y=604x-4x-5y=604x-4x-5y=60-4x-5y=60-4x-5y=60-4x

Next, divide both sides of the equation by $\begin{align*}-5\end{align*}$ to solve for $\begin{align*}y\end{align*}$ .
::接下来,将等式的两边除以 5 来为y 解决。

$\begin{aligned} \begin{array}{rcl} - 5 y & = & 60 - 4 x \\ \frac{\overset{1}{- 5}}{- 5} y & = & \frac{\overset{- 12}{60}}{- 5} - \frac{4}{- 5} x \\ y & = & - 12 + \frac{4}{5} x \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \text{-}5y &=& 60-4x \\ \frac{\overset{1}{\cancel{\text{-}5}}}{\cancel{\text{-}5}}y &=& \frac{\overset{\text{-}12}{\cancel{60}}}{\cancel{\text{-}5}}- \frac{4}{\text{-}5} x \\ y &=& \text{-}12+\frac{4}{5} x \end{array}\end{align*}$
::-5y=60-4x-51-5y=60-12-5-4-4-5xy=12+45x

Then, write the equation in slope-intercept form.
::然后,用斜坡界面的形式写出方程式。

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & \frac{4}{5} x - 12 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& {\color{blue}m}x+{\color{red}b} \\ y &=& {\color{blue}\frac{4}{5}}x- {\color{red}12} \\ \end{array}\end{align*}$
::y=mx+by=45x-12 y=mx+by=45x-12

The slope of the line is $\begin{align*}\frac{4}{5}\end{align*}$ and the $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}\text{-}12\end{align*}$ .
::线的斜坡是45, y 拦截是 - 12。

Review
::回顾

Use what you have learned to complete each task.
::利用你学到的东西来完成每一项任务。

$\begin{aligned} 2 x + 2 y = 8 \end{aligned}$
$\begin{align*}2x + 2y = 8\end{align*}$
::2x+2y=8

1. Write this equation in slope-intercept form.
::1. 以斜坡界面形式写出这一方程。

2. What is the slope?
::2. 什么是斜坡?

3. What is the $\begin{align*}y\end{align*}$ -intercept?
::3. 什么是Y - 接口?

4. Graph the equation.
::4. 绘制方程图。

$\begin{aligned} 3 x + 6 y = 2 \end{aligned}$
$\begin{align*}3x + 6y = 2\end{align*}$
::3x+6y=2

5. Write the following equation in slope-intercept form.
::5. 以斜坡拦截形式写下下列方程。

6. What is the slope?
::6. 什么是斜坡?

7. What is the $\begin{align*}y\end{align*}$ -intercept?
::7. 什么是Y的接口?

8. Graph the equation.
::8. 绘制方程。

Use what you have learned to solve each problem.
::利用你学到的东西解决每个问题

Miguel wants to save money to buy a new video game. He received $20 as a gift and gets $4 per week for allowance.
::Miguel想省钱买新游戏,他收到20美元的礼物,每周领取4美元的津贴。

9. Write an equation in slope-intercept form that represents this situation.
::9. 以斜坡拦截形式写一个反映这种情况的方程式。

10. How long will it take him to save enough money to buy the game if it costs $47.
::10. 如果游戏费用为47美元,他要花多长时间才能节省足够的钱买下游戏。

11. What is the slope of this line: $\begin{align*}y = 0.8x + 3\end{align*}$
::11. 这一线的坡度是多少:y=0.8x+3

12. Which form is the equation written in?
::12. 方程式以何种形式写成?

13. What is the $\begin{align*}y\end{align*}$ -intercept of this line?
::13. 这条线的 Y 间隙是什么?

14. What is the graph of this line?
::14. 这条线的图表是什么?

15. Is this a linear graph? How can you tell?
::15,这是直线图吗?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

直线方形

Graphing Linear Equations ::直线方形

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Graphing Linear Equations
::直线方形

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)