课程： 9.12 图表函数使用函数符号

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

将函数标记用于图表函数

Therese has just decided to plant a cherry tree in the backyard of her summer cottage. A worker at Farmer Clem’s sold her one that was 30 inches tall. He also sold her the name of a fertilizer that would make the tree grow at a rate of 3 inches a day. How tall will the cherry tree be at the end of three weeks?
::特蕾丝刚刚决定在其暑假别墅的后院种植一棵樱桃树。克莱姆农庄的一位工人将她那棵30英寸高的樱桃树卖给了她。他还将一份肥料的名字卖给了她,这块肥料将使树以每天3英寸的速度生长。樱桃树在三周后会有多高?

Therese does not want to wait for the tree to grow to measure its height. How can she use a graph to predict the height of the tree?
::Therese不想等待树生长以测量其高度。她如何使用图表来预测树的高度 ?

In this concept, you will learn to use to graph functions.
::在此概念中,您将学会用图解函数。

Graphing Functions
::图图函数

The equation of a straight line can be written in slope-intercept form such that $\begin{align*}(x, y)\end{align*}$ are the coordinates of a point on the line, ‘ $\begin{align*}m\end{align*}$ ’ is the of the line and ‘ $\begin{align*}b\end{align*}$ ’ is the $\begin{align*}y\end{align*}$ - intercept of the line. The equation is $\begin{align*}y=mx +b\end{align*}$ . For this function , the $\begin{align*}y\end{align*}$ -value can be represented using function notation $\begin{align*}f(x)\end{align*}$ . When function notation is used to name a function, then the function will be expressed as:
::直线的方程式可以以斜度截面的形式写成,使(x,y) 是线上点的坐标, `m ' 是线上的坐标, `b'是线上的Y。公式是 y=mx+b。对于此函数, Y 值可以用函数符号 f(x) 来表示。当函数符号用于命名函数时, 函数的表达方式是 :

\begin{aligned} f (x) = m x + b \end{aligned}

$\begin{align*}f(x) = mx + b\end{align*}$
:

xx) =mx+b

When the function expressed in function notation is used for graphing, the $\begin{align*}y\end{align*}$ -axis should be labeled as the $\begin{align*}f(x)\end{align*}$ axis. The dependent variable is ‘ $\begin{align*}y\end{align*}$ ’ $\begin{align*}f(x)\end{align*}$ and the independent variable is ‘ $\begin{align*}x\end{align*}$ ’. This means that the value for the independent variable is the ‘input’ number and the value for the dependent variable is the ‘output’ number. The value of ‘ $\begin{align*}y\end{align*}$ ’ depends upon the value of ‘ $\begin{align*}x\end{align*}$ ’.
::当函数符号中表达的函数用于图形时, Y 轴应标为 f(x) 轴。依附变量是 y , 独立变量是 `x ' 。这意味着独立变量的值是 `投入 ' 数, 依附变量的值是 `输出 ' 数。 “y” 值取决于 x 值。

Let’s look at an example.
::让我们举个例子。

Rewrite the following graph using function notation and graph the new function on a Cartesian grid.
::使用函数符号重写下图,并在笛卡尔网格上绘制新函数图。

\begin{aligned} y = - \frac{2}{3} x + 6 \end{aligned}

$\begin{align*}y = -\frac{2}{3} x +6\end{align*}$
::y 23x+6

First, replace the ‘ $\begin{align*}y\end{align*}$ ’ with the function notation $\begin{align*}f(x)\end{align*}$ .
::首先,将“y”改为函数编号f(x)。

\begin{aligned} \begin{array}{rcl} y & = & - \frac{2}{3} x + 6 \\ f (x) & = & - \frac{2}{3} x + 6 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& -\frac{2}{3} x +6 \\ f(x) &=& - \frac{2}{3} x +6 \end{array}\end{align*}$
::y23x+6f( x)\\\\\\\\\\\\\\\\\\\\+6

Next, plot the function on the Cartesian grid. Plot the point $\begin{align*}(0, 6)\end{align*}$ on the $\begin{align*}f(x)\end{align*}$ axis. From this point move horizontally 3 units right, downward 2 units and plot a point.
::下一步, 在笛卡尔网格上绘制函数。在 f( x) 轴上绘制点( 0, 6) 。从此点向右水平移动 3 个单位, 向下移动 2 个单位, 并绘制一个点。

\begin{aligned} f (x) = - \frac{2}{3} x + 6 \end{aligned}

$\begin{align*}f(x) = - \frac{2}{3} x +6\end{align*}$
:

xx)23x+6

Then, join the two plotted points with a straight line.
::然后,你们用一条直线,和那两条划线的两条划线,一起划入其中。

A linear function can also be used to represent the ordered pairs given in a t-table. Joey works for a call center where he is paid $30.00 a day plus a fixed bonus for each new internet contract he sells. The following t-table shows the number of internet contracts he sold for the first five days he worked and the amount of money he earned.
::线性函数也可以用来代表在t-table中给出的定购对子。 Joey在呼叫中心工作,每天领取$30,000美元,加上他销售的每份新的互联网合同的固定奖金。以下的table显示他头五天出售的互联网合同数量以及他赚到的钱。

*$\begin{align}x\end{align}$ (contracts sold)*	*$\begin{align}y\end{align}$ (money earned $)*
10	77.50
15	101.25
20	125.00
25	148.75
30	172.50

First, choose and name two ordered pairs from the table and use them to calculate the equation of the line.
::首先,从表格中选择两对有顺序的对,并命名其名称,用它们来计算线的方程。

\begin{aligned} (\begin{matrix} x_{1}, & y_{1} \\ 20, & 125 \end{matrix}) and (\begin{matrix} x_{2}, & y_{2} \\ 25, & 148.75 \end{matrix}) \end{aligned}

$\begin{align*}\begin{pmatrix} x_1, & y_1 \\ 20, & 125 \end{pmatrix} \ \text{and} \ \begin{pmatrix} x_2, & y_2 \\ 25, & 148.75 \end{pmatrix}\end{align*}$
:

x1,y120,125)和(x2,y225,148.75)

Next, using the two named points substitute the values into the formula to calculate the slope of the line.
::其次,使用两个点来替换公式中的值,以计算线的斜度。

\begin{aligned} \begin{array}{rcl} m & = & \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ m & = & \frac{148.75 - 125.00}{25 - 20} \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} m &=& \frac{y_2 - y_1}{x_2 - x_1} \\ m &=& \frac{148.75 - 125.00}{25-20} \end{array}\end{align*}$
::my2-y1x2-x1m=148.75-125.0025-20

Next, evaluate the formula to determine the value of the slope ‘ $\begin{align*}m\end{align*}$ ’.
::其次,评估公式以确定斜坡 ' m ' 的价值。

\begin{aligned} \begin{array}{rcl} m & = & \frac{23.75}{5} \\ m & = & 4.75 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} m &=& \frac{23.75}{5} \\ m &=& 4.75 \end{array}\end{align*}$
::m=23.755米=4.75

Next, substitute into the equation of a line written in slope-intercept form, the value of the slope.
::其次,将斜坡的值替换为以斜坡拦截形式写成的线的方程。

\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & 4.75 x + b \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& mx +b \\ y &=& 4.75 x +b \end{array}\end{align*}$
::y=mx+by=4.75x+b y=mx+by=4.75x+b

Next, substitute the value of the $\begin{align*}y\end{align*}$ -intercept into the equation. The value of ‘ $\begin{align*}b\end{align*}$ ’ is 30.00 per day.
::其次,将 Y 界面的值替换到方程中。 " b " 值为每天30.00。

\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & 4.75 x + b \\ y & = & 4.75 x + 30 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& mx +b \\ y &=& 4.75 x +b \\ y &=& 4.75 x +30 \end{array}\end{align*}$
::y=mx+by=4.75x+by=4.75x+by=4.75x+30

Then, express the equation of the line using function notation and graph it.
::然后用函数符号表示线条的方程式,然后用图示来表示线条的方程式。

\begin{aligned} \begin{array}{rcl} y & = & 4.75 x + 30 \\ f (x) & = & 4.75 x + 30 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 4.75 x +30 \\ f(x) &=& 4.75 x +30 \end{array}\end{align*}$
::y=4.75x+30f(x)=4.75x+30

Examples
::实例

Example 1
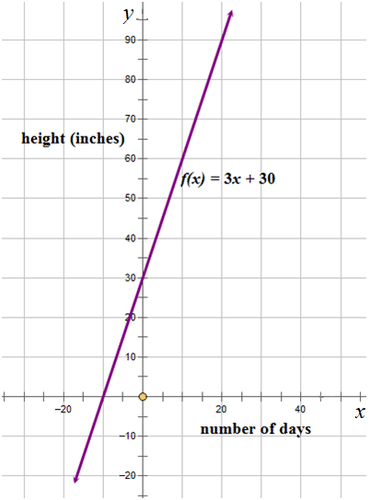
::例1

Earlier, you were given a problem about Therese and the cherry tree. She wants to show the height of the tree using a graph. How can Therese do this?
::早些时候,有人给了你关于Therese和樱桃树的问题。她想用图表显示树的高度。Therese怎么能这样做呢?

Therese can use a function expressed in function notation and plot the function on a Cartesian grid.
::特蕾斯可以使用函数符号表达的函数,并在笛卡尔网格上绘制函数。

First, write down the given information.
::首先,写下给定的信息。

$\begin{align*}y\end{align*}$ = height of the tree at the end of three weeks
::y = 3周结束时树的高度。

$\begin{align*}m\end{align*}$ = rate the tree grows each day $\begin{align*}\rightarrow \frac{3 \ \text{inches}}{1 \ \text{day}} = 3\end{align*}$
::m = 树的生长速度每天3英寸1天=3

$\begin{align*}x\end{align*}$ = number of days
::x=天数

$\begin{align*}b\end{align*}$ = height of tree when purchased $\begin{align*}\rightarrow 30 \ \text{inches}\end{align*}$
::b = 购买时树高30英寸

Next, write an equation, in slope-intercept form, to represent the given information.
::接下来,写一个方程,以斜坡界面的形式,代表给定的信息。

\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & 3 x + 30 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& mx +b \\ y &=& 3x+30 \end{array}\end{align*}$
::y=mx+by=3x+30 y=mx+by=3x+30

Next, express the equation using function notation. Replace ‘ $\begin{align*}y\end{align*}$ ’ using $\begin{align*}f(x)\end{align*}$ notation.
::接下来,使用函数符号表示方程式。用 f(x) 符号替换“y”。

\begin{aligned} \begin{array}{rcl} y & = & 3 x + 30 \\ f (x) & = & 3 x + 30 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 3x+30 \\ f(x) &=& 3x+30 \end{array}\end{align*}$
::y=3x+30f(x)=3x+30

Then, graph the function
::然后,图形显示函数

\begin{aligned} f (x) = 3 x + 30 \end{aligned}

$\begin{align*}f(x) = 3x+30\end{align*}$
:

xx)=3x+30

From the graph it can be seen that the height of the tree at the end of three weeks will be slightly greater than 90 inches. Remember three weeks is equivalent to 21 days.
::从图中可以看出,树在三个星期结束时的高度将略高于90英寸。记住三个星期相当于21天。

Example 2
::例2

Rewrite the linear function using function notation and graph the line.
::使用函数符号重写线性函数,并绘制线条图。

\begin{aligned} y = 3 x + 2 \end{aligned}

$\begin{align*}y = 3x+2\end{align*}$
::y=3x+2 y=3x+2

First, replace the ‘ $\begin{align*}y\end{align*}$ ’ using function notation $\begin{align*}f(x)\end{align*}$ .
::首先,用函数编号f(x)替换“y”。

\begin{aligned} \begin{array}{rcl} y & = & 3 x + 2 \\ f (x) & = & 3 x + 2 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& 3x+2 \\\ f(x) &=& 3x+2 \end{array}\end{align*}$
::y=3x+2 f( x)=3x+2

Then, graph the function.
::然后,绘制函数图。

\begin{aligned} f (x) = 3 x + 2 \end{aligned}

$\begin{align*}f(x) = 3x+2\end{align*}$
:

xx)=3x+2

Example 3
::例3

Identify the slope and the $\begin{align*}y\end{align*}$ -intercept for the following linear function.
::标明以下线性函数的斜坡和 Y 界面。

\begin{aligned} y = \frac{8}{9} x - \frac{1}{3} \end{aligned}

$\begin{align*}y = \frac{8}{9} x - \frac{1}{3}\end{align*}$
::y=89x-13 y=89x-13

First, name the form in which the function is written.
::首先,指定撰写函数的表格。

Slope-intercept form
::斜缩截截面窗体

Next, write the general form for a function written in slope-intercept form.
::下一步,写上以斜坡界面格式撰写的函数的一般格式。

\begin{aligned} y = m x + b \end{aligned}

$\begin{align*}y= mx+b\end{align*}$
::y=mx+b y=mx+b

Then, state the slope and $\begin{align*}y\end{align*}$ -intercept of the line.
::然后指出斜坡和横线的 Y 插口。

\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & \frac{8}{9} x - \frac{1}{3} \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& {\color{blue}m}x +{\color{red}b} \\ y &=& \frac{{\color{blue}8}}{{\color{blue}9}} x {\color{red}-}{\color{red}\frac{1}{3}} \end{array}\end{align*}$
::y=mx+by=89x-13 y=mx+by=89x-13

The answer is $\begin{align*}\frac{8}{9}\end{align*}$ and $\begin{align*}-\frac{1}{3}\end{align*}$ .
::答案是89和13

The slope of the line is $\begin{align*}\frac{8}{9}\end{align*}$ and the $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}-\frac{1}{3}\end{align*}$ .
::线的斜坡是89, y-interview是- 13。

Example 4
::例4

Express the following equation using function notation.
::使用函数符号表示以下方程式。

\begin{aligned} y = - \frac{3}{4} x + 9 \end{aligned}

$\begin{align*}y = -\frac{3}{4} x +9\end{align*}$
::y34x+9

First, replace the ‘ $\begin{align*}y\end{align*}$ ’ with function notation.
::首先,将“y”改为函数符号。

\begin{aligned} \begin{array}{rcl} y & = & - \frac{3}{4} x + 9 \\ f (x) & = & - \frac{3}{4} x + 9 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& - \frac{3}{4} x +9 \\ f(x) &=& - \frac{3}{4} x +9 \end{array}\end{align*}$
::y34x+9f( x)\\\\\\\\\34x+9

The answer is $\begin{align*}f(x) = -\frac{3}{4} x +9\end{align*}$ .
::答案是 f(x)\\\\\\\\\\\\\\\\\\\\\\\\\"34x+9\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\F\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Example 5
::例5

Identify the slope and the $\begin{align*}y\end{align*}$ -intercept for the following linear function.
::标明以下线性函数的斜坡和 Y 界面。

\begin{aligned} f (x) = \frac{1}{2} x - 8 \end{aligned}

$\begin{align*}f(x) = \frac{1}{2} x -8\end{align*}$
:

xx)=12x-8)

First, name the form in which the function is written.
::首先,指定撰写函数的表格。

Slope-intercept form using function notation.
::使用函数符号的斜坡截取表单。

Next, write the general form for a function written in slope-intercept form.
::下一步,写上以斜坡界面格式撰写的函数的一般格式。

\begin{aligned} f (x) = m x + b \end{aligned}

$\begin{align*}f(x) = mx+b\end{align*}$
:

xx) =mx+b

Then, state the slope and $\begin{align*}y\end{align*}$ -intercept of the line.
::然后指出斜坡和横线的 Y 插口。

\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ f (x) & = & m x + b \\ f (x) & = & \frac{1}{2} x - 8 \end{array} \end{aligned}

$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ f(x) &=& {\color{blue}m} x+{\color{red}b} \\ f(x) &=& \frac{{\color{blue}1}}{{\color{blue}2}} x {\color{red}-8} \end{array} \end{align*}$
::y=mx+bf(x)=mx+bf(x)=12x-8

The answer is $\begin{align*}\frac{1}{2}\end{align*}$ and -8.
::答案是12和8。

The slope of the line is $\begin{align*}\frac{1}{2}\end{align*}$ and the $\begin{align*}y\end{align*}$ -intercept is -8.
::线的斜坡是12, y 接口是 - 8 。

Review
::回顾

Graph each function.
::每个函数图示。

1. $\begin{align*}f(x) = 3x+1\end{align*}$
::1. f(x)=3x+1

2. $\begin{align*}f(x) = 2x+2\end{align*}$
::2. f(x)=2x+2

3. $\begin{align*}f(x) = 5x-1\end{align*}$
::3. f(x)=5x-1

4. $\begin{align*}f(x) = x-3\end{align*}$
::4. f(x)=x-3

5. $\begin{align*}f(x) = -2x+1\end{align*}$
::5. f(x)%2x+1

6. $\begin{align*}f(x) = -2x-5\end{align*}$
::6. f(x)%%2x-5

7. $\begin{align*}f(x) = -4x+9\end{align*}$
::7. f(x)4x+9

8. $\begin{align*}f(x) = 4x+8\end{align*}$
::8. f(x)=4x+8

9. $\begin{align*}f(x) = x-10\end{align*}$
::9. f(x)=x-10

10. $\begin{align*}f(x) =2x+6\end{align*}$
::10. f(x)=2x+6

Use what you have learned to solve each problem.
::利用你学到的东西解决每个问题

11. A migrating monarch butterfly travels 1100 miles. If it flies 30 miles per day, the distance $\begin{align*}d\end{align*}$ it still has to travel is a function of days $\begin{align*}t\end{align*}$ it has traveled. Write a function rule for the situation.
::11. 一位迁徙的君主蝴蝶旅行1100英里,如果每天飞行30英里,那么它仍然必须旅行的距离是它旅行的天数的函数。

12. What is the slope of the situation?
::12. 局势的斜坡是什么?

13. A writer gets paid a writer’s fee of $3000 plus $1.50 for each copy of the book that is sold. Create a function rule for this situation.
::13. 向作家支付作家费用3 000美元加上每本售出书的1.50美元,为这种情况制定功能规则。

14. What is the slope of this situation?
::14. 这种情况的斜坡是什么?

15. How many books does the writer need to sell to earn $10,000 total?
::15. 作者要卖几本书才能赚到总共10 000美元?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

将函数标记用于图表函数

Graphing Functions ::图图函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)