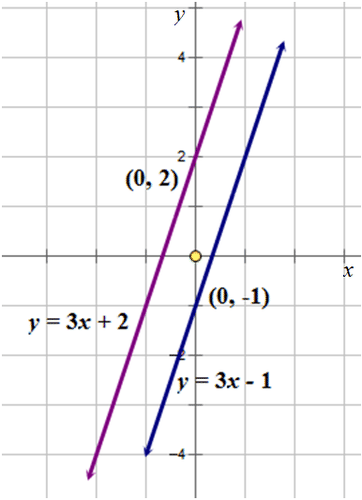Course: 9.14 通过图表绘制解决线性线性系统

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 通过图形绘制解决线性系统

Collapse Expand
通过图形绘制解决线性系统
Two trains leave the station going in the same direction. One train leaves two hours before the other one. If the first train travels at an average speed of 65 mph and the second train travels at an average speed of 90 mph, then how long will it take the second train to catch up to the first train?
::两列火车从火车站向同一方向出发,一列火车比另一列火车提前两小时离开,如果第一列火车平均飞行速度为65英里,第二列火车平均飞行速度为90英里,那么第二列火车要赶到第一列火车还要多久?

In this concept, you will learn to solve linear systems by graphing.
::在这个概念中,你会学会通过图形化解决线性系统。

Graphing Linear Systems
::线性系统

The solution for a system of two linear equations with two variables is an ordered pair that will make both equations true. If an ordered pair makes one of the linear equations true then the ordered pair represents a point on the line. If the same ordered pair makes the second linear equation true then the ordered pair represents a point on that line. If the same point is on the two lines, then the lines both pass through this same point. This means that the two lines will cross each other or intersect at this point.
::由两个变量组成的两个线性方程式的解决方案是两个线性方程式的定序对配方,它能使两个方程式都真实。如果一个定型对方对使一个线性方程式真实,那么定型对对方代表线上的一个点。如果同一定型对使第二个线性方程式真实,则定型对对方代表该线上的一个点。如果两条线上有一个相同的点,则两条线线将穿过同一个点。这意味着两条线将在此点相互交叉或交叉。

A system of equations can have one solution, no solution or an infinite number of solutions.
::一个方程式系统可以有一个解决办法,没有解决办法,或无穷无尽的解决办法。

Solve the following system of linear equations by graphing.
::通过图形化解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} y & = & 2 x - 4 \\ y & = & - 2 x + 8 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& 2x-4 \\ y &=& -2x+8 \end{array}\end{align*}$
::y=2x-4y=2x+8

Notice that both equations are written in slope- intercept form $\begin{align*}y=mx+b\end{align*}$ .
::注意两个方程式都是以 y=mx+b 的斜度界面写成的。

First, write down the information given in each equation .
::首先,写下每个方程式中给出的信息。

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & 2 x - 4 \\ m & = & 2; b = - 4 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& 2x-4 \\ m &=& 2; b = -4 \end{array}\end{align*}$
::y=mx+by=2x-4m=2;b=4

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & - 2 x + 8 \\ m & = & - 2; b = 8 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& -2x+8 \\ m &=& -2; b=8 \end{array}\end{align*}$

::y=mx+by=%2x+8m=2;b=8

Next, graph each of the equations on the same Cartesian grid.
::下一张图每一个方程式都在同一条笛卡尔的网格上

The two lines intersect at the point $\begin{align*}(3,2)\end{align*}$ .
::两条线在点(3,2)交叉。

The solution is $\begin{align*}\dbinom{x}{y} = \dbinom{3}{2}\end{align*}$ .
::解决方案是 (xy) = (32) 。

Solve the following system of linear equations by graphing.
::通过图形化解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} y & = & 3 x - 1 \\ y & = & 3 x + 2 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& 3x-1 \\ y &=& 3x+2 \end{array}\end{align*}$
::y=3x- 1y=3x+2 y=3x+2

Notice that both equations are written in slope-intercept form $\begin{align*}y=mx+b\end{align*}$ .
::注意两个方程式都是以 y=mx+b 的斜度界面写成的。

First, write down the information given in each equation.
::首先,写下每个方程式中给出的信息。

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & 3 x - 1 \\ m & = & 3; b = - 1 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& 3x-1 \\ m &=& 3; b=-1 \end{array}\end{align*}$
::y=mx+by=3x-1m=3;b=1

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & 3 x + 2 \\ m & = & 3; b = 2 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& 3x+2 \\ m &=& 3; b=2 \end{array}\end{align*}$
::y=mx+by=3x+2m=3;b=2

The equations have the same slopes but different $\begin{align*}y\end{align*}$ - intercepts .
::方程式有相同的斜坡,但有不同的 Y 界面。

Next, graph each of the equations on the same Cartesian grid.
::下一张图每一个方程式都在同一条笛卡尔的网格上

The lines are parallel which means they will never intersect. There is no solution for this system of equations.
::线条是平行的, 这意味着它们永远不会交叉。对于这个方程式系统, 没有任何解决办法。

Solve the following system of linear equations by graphing.
::通过图形化解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} y & = & - \frac{1}{4} x - 1 \\ x + 4 y & = & - 4 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& - \frac{1}{4} x -1 \\ x+4y &=& -4 \end{array}\end{align*}$
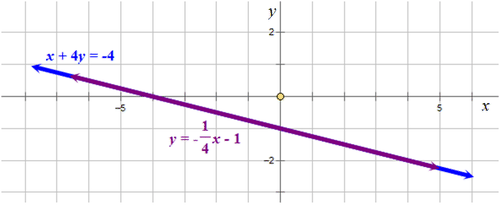
::y14x- 1x+4y4

First, write down the information given in each equation.
::首先,写下每个方程式中给出的信息。

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & - \frac{1}{4} x - 1 \\ m & = & - \frac{1}{4}; b = - 1 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& -\frac{1}{4}x-1 \\ m &=& -\frac{1}{4}; b=-1 \end{array}\end{align*}$
::y=mx+by=14x_1m}14;b=1

$\begin{aligned} \begin{array}{rcl} x + 4 y & = & - 4 written in standard form A x + B y = C \\ x - intercept & = & (- 4, 0) \\ y - intercept & = & (0, - 1) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} x+4y &=& -4 \qquad \text{written in standard form} \ Ax+By=C \\ x- \text{intercept} &=& (-4,0) \\ y- \text{intercept} &=& (0,-1) \end{array}\end{align*}$
::x+4y4 以标准格式Ax+By=Cx-截取=(- 4,0)y- 截取=(0,-1)写成

The second equation is a multiple $\begin{align*}(4)\end{align*}$ of the first equation.
::第二个方程式是第一个方程式的倍数(4)。

Next, graph each of the equations on the same Cartesian grid.
::下一张图每一个方程式都在同一条笛卡尔的网格上

The lines coincide which means they are actually the graph of the same line. There are an infinite number of solutions for this system of equations.
::线条的重合表示它们实际上是同一线条的图形。对于这个方程式系统,有无限数量的解决方案。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the two trains that left the station at different times. The second train left two hours after the first train but was travelling at a greater speed than the first train. You need to figure out when the second train will catch up to the first train.
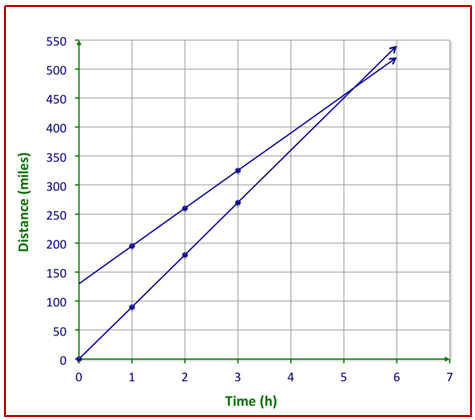
::早些时候,您遇到两列火车在不同的时间离开火车站的问题。第二列火车在第一班火车后两小时离开,但速度比第一班火车要快。您需要弄清楚第二班火车何时会赶上第一班火车。

First, write a system of linear equations to represent the distance travelled by each of the trains. Remember that distance $\begin{align*}(d)\end{align*}$ is a function of the product of speed $\begin{align*}(s)\end{align*}$ and time $\begin{align*}(t)\end{align*}$ .
::首先, 写入一个线性方程系统, 以表示每列列列的距离。记住, 距离( d) 是速度( s) 和时间( t) 的函数。

$\begin{aligned} \begin{array}{rcl} d & = & s t \\ Train 1 : d & = & 65 (t + 2) \\ d & = & 65 t + 130 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& st\\ \text{Train }1: d &=& 65(t+2) \\ d &=& 65t+130 \end{array}\end{align*}$
::d=培训1:d=65(t+2)d=65t+130

$\begin{aligned} \begin{array}{rcl} d & = & s t \\ Train 2 : d & = & 90 t \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} d &=& st \\ \text{Train } 2 : d &=& 90t \end{array}\end{align*}$
::d= 培训2:d=90t

Next, graph the two equations on the same Cartesian grid.
::下一位,请绘制两个方程式的图在同一的笛卡尔网格上。

The lines display an intersection point just past five hours. This means the two trains will catch up with each other at this point.
::线条显示一个交叉点刚刚过五小时。这意味着两列列列车将会在这一点上赶上来。

Solve the following system of linear equations by graphing:
::以图示方式解决下列线性方程式系统:

$\begin{aligned} \begin{array}{rcl} 2 x + 3 y & = & 4 \\ x - 5 y & = & - 11 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 2x+3y &=& 4 \\ x-5y &=& -11 \end{array}\end{align*}$
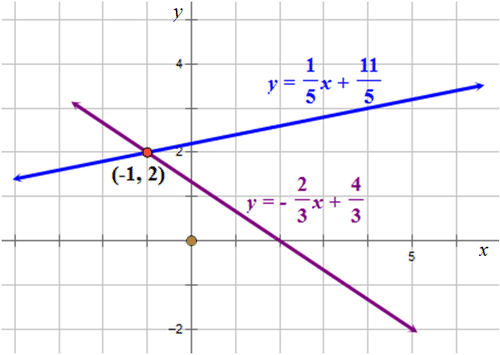
::2+3y=4x-5y11

Both equations are written in standard form $\begin{align*}Ax+By=C\end{align*}$ .
::两种方程式均以标准格式Ax+By=C书写。

First, write each equation in slope-intercept form $\begin{align*}y=mx+b\end{align*}$ and write down the value of the and the $\begin{align*}y\end{align*}$ -intercept.
::首先,以 y=mx+b 格式写下每个方程式, 并写下该方程式和 y 界面的值。

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & - \frac{2}{3} x + \frac{4}{3} \\ m & = & - \frac{2}{3}; b = \frac{4}{3} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& -\frac{2}{3}x+\frac{4}{3} \\ m &=& -\frac{2}{3}; b=\frac{4}{3} \end{array}\end{align*}$
::y=mx+by=%23x+43m=23;b=43

$\begin{aligned} \begin{array}{rcl} y & = & m x + b \\ y & = & \frac{1}{5} x + \frac{11}{5} \\ m & = & \frac{1}{5}; b = \frac{11}{5} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} y &=& mx+b \\ y &=& \frac{1}{5}x+\frac{11}{5} \\ m &=& \frac{1}{5}; b=\frac{11}{5} \end{array}\end{align*}$
::y=mx+by=15x+115m=15;b=115

Then, graph both equations on the same Cartesian grid.
::然后用同一个笛卡尔网格绘制两个方程式的图表

The two lines intersect at the point $\begin{align*}(-1,2)\end{align*}$ . The solution for this system of linear equations is:
::两条线在点(-1,2)交叉,这一线性方程式系统的解决方案是:

$\begin{aligned} (\binom{x}{y}) = (\binom{- 1}{2}) \end{aligned}$
$\begin{align*}\dbinom{x}{y} = \dbinom{-1}{2}\end{align*}$
:xy)=(-12)

Answer the following examples using True or False. If the answer is false, explain why.
::使用 True 或 False 回答以下例子。如果答案是假的, 请解释原因。

Example 2
::例2

If two lines intersect at one point, then the coordinates of that point are the solution to the linear system.
::如果两条线在一个点交叉,那么该点的坐标就是线性系统的解决方案。

The answer is true.
::答案是真实的。

Example 3
::例3

If a system of linear equations is such that both equations have the same slope but different $\begin{align*}y\end{align*}$ -intercepts then there are an infinite number of solutions for the linear system.
::如果一个线性方程式系统使两个方程式都具有相同的斜度,但相互之间的距离不同,那么线性系统就有无限数量的解决方案。

The answer is false.
::答案是虚假的。

If two equations have the same slope then the graph of the equations will display two parallel lines with different $\begin{align*}y\end{align*}$ -intercepts. Parallel lines will never intersect. There is no solution for this linear system.
::如果两个方程式的斜度相同, 则方程式的图形将显示两条带有不同 Y 界面的平行线。平行线条永远不会交叉。这个线性系统没有解决方案。

Example 4
::例4

If a system of linear equations is such that the two lines coincide then there is no solution for the linear system.
::如果线性方程式系统使两行重合,那么线性系统就没有解决办法。

The answer is false.
::答案是虚假的。

If the graph of the linear system displays two lines that coincide then every ordered pair is on both lines and satisfy both equations. There is an infinite number of solutions for the linear system.
::如果线性系统的图形显示两行相同,那么每对定购的一对在两条线上,满足了两个方程。线性系统有无限数量的解决方案。

Review
::回顾

Graph the following systems of equations. Identify the solution or write no solution or infinitely many solutions, if appropriate.
::如下方程系统图解。确定解决方案, 或者酌情写入无解决方案或无限多的解决方案。

1. $\begin{align*}\begin{array}{rcl} y &=& 2x-3 \\ y &=& x-1 \end{array}\end{align*}$
::1. y=2x-3y=x-1

2. $\begin{align*}\begin{array}{rcl} 2x+2y &=& 1 \\ y &=& -x+\frac{1}{2} \end{array}\end{align*}$

::2. 2x+2y=1yx+12

3. $\begin{align*}\begin{array}{rcl} y &=& -3x+1 \\ 3x-y &=& -7 \end{array}\end{align*}$
::3. y3x+13x-y7

4. $\begin{align*}\begin{array}{rcl} y &=& 2x \\ \frac{y}{2} &=& x - \frac{5}{2} \end{array}\end{align*}$
::4. y=2xy2=x-52

5. $\begin{align*}\begin{array}{rcl} y&=&3x+5 \\ y&=&-3x+8 \end{array}\end{align*}$

::5. y=3x+5y=3x+5y=3x+8

6. $\begin{align*}\begin{array}{rcl} y&=&2x+1 \\ y&=&3x+3 \end{array}\end{align*}$

::6. y=2x+1y=3x+3

7. $\begin{align*}\begin{array}{rcl} y&=&\frac{1}{2}x-2 \\ y&=&-2x \end{array}\end{align*}$
::7. y=12x-2y=2y=2x

8. $\begin{align*}\begin{array}{rcl} y &=& -2x+1 \\ y&=&-2x-2 \end{array}\end{align*}$
::8. y2x+1y2x-2

9. $\begin{align*}\begin{array}{rcl} y&=&4x-1 \\ y&=&2x+2 \end{array}\end{align*}$
::9 y= 4x- 1y= 2x+2

10. $\begin{align*}\begin{array}{rcl} y &=&5x-3 \\ y&=&-5x+1 \end{array}\end{align*}$
::10. y=5x-3y=5x+1

11. $\begin{align*}\begin{array}{rcl} y&=&2x \\ y &=&3x-5 \end{array}\end{align*}$
::11. y=2xy=3x-5

12. $\begin{align*}\begin{array}{rcl} y&=&-x-1 \\ y&=&-x+6 \end{array}\end{align*}$
::12. yx-1yx+6

Answer each question true or false.
::回答每个问题是否真实或虚假。

13. Some linear systems do not have a solution.
::13. 有些线性系统没有解决办法。

14. Perpendicular lines have one solution.
::14. 直直线有一个解决办法。

15. Lines with the same slope and $\begin{align*}y\end{align*}$ -intercept have infinite solutions.
::15. 具有同一坡度和Y交界线的线有无限的解决办法。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

通过图形绘制解决线性系统

Graphing Linear Systems ::线性系统

Solve the following system of linear equations by graphing. ::通过图形化解决下列线性方程系统。

Solve the following system of linear equations by graphing. ::通过图形化解决下列线性方程系统。

Solve the following system of linear equations by graphing. ::通过图形化解决下列线性方程系统。

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Graphing Linear Systems
::线性系统

Solve the following system of linear equations by graphing.
::通过图形化解决下列线性方程系统。

Solve the following system of linear equations by graphing.
::通过图形化解决下列线性方程系统。

Solve the following system of linear equations by graphing.
::通过图形化解决下列线性方程系统。

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)