Course: 12.6 减减多面体 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 减减多元数

Collapse Expand
减减多元数
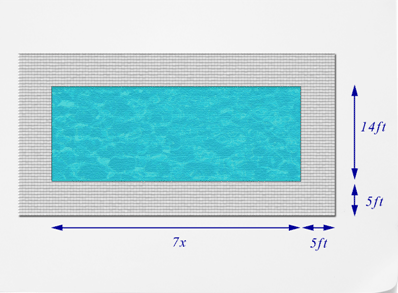
A concrete walkway surrounds a rectangular swimming pool. In order to know how much weather treatment to buy, the owner must know how many square units of concrete he has. The walkway is 5 feet wide on all sides. The swimming pool has a length of $\begin{align*}7x\end{align*}$ and a width of 14 feet. How many square units of concrete does he have?
::水泥行道环绕着长方形游泳池。要知道要购买多少天气治疗, 车主必须知道他有多少平方体混凝土。路道四面宽5英尺。游泳池长7x,宽14英尺。他有多少平方体混凝土?

In this concept, you will learn to subtract .
::在这个概念中,你会学会减。

Subtracting Polynomials
::减减多元数

A polynomial is an algebraic expression that shows the sum of monomials. Just like you can add polynomials, you can subtract them too. You can perform this operation both vertically and horizontally . Let’s start with vertically.
::多面体是一个代数表达式,它显示单面体的总和。就像您可以添加多面体一样,您也可以将其也减去。您可以垂直和水平执行此操作。让我们从垂直开始。

One point to remember is that subtraction is the same as “adding the opposite.” In other words, $\begin{align*}5 - 8\end{align*}$ is the same as $\begin{align*}5 + (-8)\end{align*}$ . You can add the opposite of 8 instead of subtracting 8. You will use the same idea with polynomials.
::需要记住的一点是,减法与“增加反差”相同。换句话说,5-8与5+(-8)相同,您可以加上相反的8,而不是减去8。您会用同一想法来对待多义。

Let’s look at an example.
::让我们举个例子。

Subtract the polynomials $\begin{align*}(9x^2 + 4x - 7)\end{align*}$ and $\begin{align*}(2x^2 + 6x - 4)\end{align*}$ .
::减去多数值(9x2+4x-7)和2x2+6x-4)。

First, line up the like terms so that you can subtract them vertically.
::首先,排列类似条件,以便垂直减法。

$\begin{aligned} \begin{array}{rcl} 9 x^{2} + 4 x - 7 \to 9 x^{2} + 4 x + - 7 Lines up like terms \\ \underline{- 2 x^{2} + 6 x - 4 \to - 2 x^{2} + - 6 x + 4} \underline{Add the opposite} \\ 7 x^{2} - 2 x - 3 \leftarrow 7 x^{2} + - 2 x + - 3 Combine lilke terms \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} && \quad 9x^2+4x-7 \quad \rightarrow \ \ \quad 9x^2 \quad + \ \ \quad 4x \quad + \quad -7 \quad \text{Lines up like terms} \\ && \underline{-2x^2+6x-4 \quad \rightarrow \quad -2x^2 \quad + \quad -6x \quad + \ \quad 4} \quad \ \underline{\text{Add the opposite} \quad \ \ } \\ && \quad 7x^2-2x-3 \quad \ \ \leftarrow \quad \ \ 7x^2 \quad + \ \quad -2x + \ -3 \quad \ \ \ \text{Combine lilke terms} \end{array}\end{align*}$
::9x2+4x-7 9x2+4x2+4x77Lines 类似条件 - 2x2+6x-42x2x22x6x+4_ 加上相反的 _7x2-2-2x-3 7x2+-2x+-2x+-3

When you add the opposite the sign changes on each of the terms in the subtracted polynomial. Inside the " data-term="Parentheses" role="term" tabindex="0"> parentheses , the coefficient of $\begin{align*}2x^2\end{align*}$ is positive. But when you add the opposite, the sign changes to negative, or $\begin{align*}-2x^2\end{align*}$ . You also changed the sign on the $\begin{align*}6x\end{align*}$ to $\begin{align*}-6x\end{align*}$ and the -4 to 4.
::当您在减法多面体中的每个条件中添加相反的符号变化时,括号内2x2的系数是正数。但是,在反面增加时,符号变化为负数,或-2-2x2。您还将 6x 上的符号修改为-6x 和 -4 至 4。

Now you can look at subtracting polynomials horizontally.
::现在您可以横向查看多边数字的减法。

You just learned to subtract polynomials vertically. You can also subtract polynomials horizontally. First you will need to review the .
::您刚刚学会垂直减减多数值。您也可以水平减减多数值。首先您需要查看。

$\begin{aligned} x^{2} - 8 \end{aligned}$
$\begin{align*}x^2 - 8\end{align*}$
::x2-8

The distributive property: For all real numbers $\begin{align*}a, b\end{align*}$ and $\begin{align*}c\end{align*}$    $\begin{align*}a(b + c) = ab + ac\end{align*}$ .
::分配财产:所有实际数字a、b和ca(b+c)=ab+ac。

$\begin{aligned} \begin{array}{rcl} 5 (3 x + 7) & = & 15 x + 35 \\ 4 (2 y - 7) & = & 8 y - 28 \\ - 2 (9 x + 3) & = & - 18 x - 6 \\ - 3 (- 2 y - 4) & = & 6 y + 12 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5(3x + 7) &=& 15x + 35 \\ 4(2y - 7) &=& 8y - 28 \\ -2(9x + 3) &=& -18x - 6 \\ -3(-2y - 4) &=& 6y + 12 \end{array} \end{align*}$
::5(3x+7)=15x+354(2y-7)=8y-28-2(9x+3)=8y-28-2(9x+3)=18x-6-3(-2y-4)=6y+12

Remember be careful with negative signs when using distributive property.
::在使用分配财产时,要小心注意负面迹象。

Remember that coefficients are the numerical factors of variables. The coefficient of $\begin{align*} 3x\end{align*}$ is 3. The coefficient of $\begin{align*}9x^2 \end{align*}$ is 9. When you see the term $\begin{align*}-x\end{align*}$ , the coefficient is -1. Although you could write $\begin{align*}-1x\end{align*}$ , you normally do not because the 1 is considered unnecessary. How does this relate to the distributive property? The negative sign could be in front of the parentheses, like this: $\begin{align*}-(3x- 2)\end{align*}$ . This is similar to $\begin{align*}-x\end{align*}$ where the coefficient is unwritten but understood to be -1. Just like you could write $\begin{align*}-1x\end{align*}$ , you could also write $\begin{align*}-1 (3x - 2)\end{align*}$ . The distributive property is now more apparent given that each term will now be multiplied by -1.
::记住系数是变量的数值系数。 3x的系数是3。 9x2的系数是9。当你看到-x的术语时, 9x2的系数是-1. 。尽管您可以写- 1x, 但通常您不会写- 1x。这与分配属性有什么关系? 负符号可能在括号前面, 比如 : - (3x-2) 。这类似于-x, 系数是不成文的, 但被理解为 - 1. 1x 。正如您可以写- 1x, 您也可以写- 1(3x-2) 。分配属性现在更加明显, 因为每个术语现在都会乘以 - 1 。

Take a look at the following applications of the distributive property.
::研究分配财产的下列应用。

$\begin{aligned} \begin{array}{rcl} - (7 x + 5) & = & - 1 (7 x - 5) \\ = & - 7 x - 5 \\ - (x^{2} - 3 x + 14) & = & - 1 (x^{2} - 3 x + 14) \\ = & - x^{2} + 3 x - 14 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} -(7x + 5) &=& -1(7x - 5) \\ &=& -7x - 5 \\ -(x^2 - 3x + 14) &=& -1(x^2 - 3x + 14) \\ &=& -x^2 + 3x - 14 \end{array}\end{align*}$
::- (7x+5) 1(7x-5) 7x-5-(x2-3x+14) 1(x2-3x+14) x2+3x+14) x2+3x-14

Here the -1 has been inserted and then the multiplication has been performed. As with adding the opposite, the sign changes on each of the terms in the polynomial.
::在这里插入了 - 1 , 然后进行了乘法。与增加相反, 多义中每个词的符号修改相同。

You can now use this method to subtract polynomials horizontally. First you will distribute the negative sign to each of the terms in the subtracted polynomial and then you will combine like terms.
::现在您可以使用这个方法水平地减去多多边数。首先, 您会将负符号分布到减入多多边数中的每个词中, 然后将相同的词组合在一起。

Subtract the polynomials $\begin{align*}(5x+3)\end{align*}$ and $\begin{align*}(2x - 8)\end{align*}$ .
::减号(5x+3)和(2x-8)。

First, rewrite the polynomials without parentheses. Remember that subtracting is adding the opposite.
::首先, 在没有括号的情况下重写多面体。记住减法是增加反面的。

$\begin{aligned} (5 x + 3) - (2 x - 8) = 5 x + 3 - 2 x + 8 \end{aligned}$
$\begin{align*}( 5x + 3) - (2x - 8) = 5x + 3 - 2x + 8\end{align*}$

:5x+3)-(2x-8)=5x+3-2x+8

Next, combine like terms.
::接下来,把术语合并起来。

$\begin{aligned} \begin{array}{rcl} (5 x + 3) - (2 x - 8) & = & 5 x + 3 - 2 x + 8 \\ = & 3 x + 11 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (5x + 3) - (2x - 8) &=& {\color{red}5x} + 3 - {\color{red}2x} + 8 \\ &=& {\color{red}3x} + 11 \end{array}\end{align*}$
:5x+3)-(2x-8)=5x+3-2x+8=3x+11

The answer is $\begin{align*}3x+11\end{align*}$ .
::答案是 3x+11。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the pool and the concrete.
::早些时候,你得到一个问题关于游泳池和混凝土。

First, find the area of the pool plus the walkway. The length of the large rectangle measures $\begin{align*}7x + 5 + 5\end{align*}$ . Its width measures $\begin{align*}14 + 5 + 5\end{align*}$ .
::首先,找到游泳池的面积加上步行道。大矩形的长度为 7x+5+5。它的宽度为 14+5+5。

$\begin{aligned} \begin{array}{rcl} A & = & l \times w \\ A & = & (7 x + 5 + 5) \times (14 + 5 + 5) \\ A & = & (7 x + 10) \times (24) \\ A & = & 168 x + 240 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A &=& l \times w \\ A &=& (7x + 5 + 5) \times (14 + 5 + 5) \\ A &=& (7x + 10) \times (24) \\ A &=& 168x + 240 \end{array} \end{align*}$
::A=lxxwA=(7x+5+5+5)xx(14+5+5)A=(7x+10)xx(24)A=168x+240

Next, find the area of just the swimming pool.
::下一个,找到游泳池那片区域

$\begin{aligned} \begin{array}{rcl} A & = & l \times w \\ A & = & (7 x) \times (14) \\ A & = & 98 x \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A &=& l \times w \\ A &=& (7x) \times(14) \\ A &=& 98x \end{array} \end{align*}$
::A=lxwA=( 7x) x( 14) A=98x

Then subtract the area of the pool from the area of the entire swimming area to find the area of the concrete walkway.
::然后从整个游泳区的区域中减去游泳池区域,以找到水泥通道区域。

$\begin{aligned} \begin{array}{rcl} A_{Concrete} & = & A_{swimming area} - A_{swimming pool} \\ A_{Concrete} & = & 168 x + 240 - 98 x \\ A_{Concrete} & = & 70 x + 240 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{Concrete}} & = & A_ {\text{swimming area}} - A_{\text {swimming pool}} \\ A_{\text{Concrete}} & = & 168x + 240 - 98x\\ A_{\text{Concrete}} & = & 70x + 240 \end{array}\end{align*}$
::Aconcrete = Aswimming 区域 - Aswimming 池内 AConcrete=168x+240-98xAConcrete=70x+240

The answer is $\begin{align*}70x + 240\end{align*}$ .
::答案是70x+240。

He needs $\begin{align*}70x + 240\end{align*}$ square feet of concrete.
::他需要70x+240平方英尺的混凝土

Example 2
::例2

Subtract the polynomials $\begin{align*} (-7x^3 + 3x^2 - x + 4)\end{align*}$ and $\begin{align*} (-6x^2 + 9)\end{align*}$ .
::减号数(-7x3+3x2-x+4)和(-6x2+9)

First, line up the like terms so that you can subtract them vertically.
::首先,排列类似条件,以便垂直减法。


$\begin{aligned} (- 7 x^{3} + 3 x^{2} - x + 4) \to - 7 x^{3} + 3 x^{2} + - x + 4 \\ \underline{- (- 6 x^{2} + 9) \to 6 x^{2} - 9} \end{aligned}$
$\begin{align*}& \quad (-7x^3+3x^2-x+4) \quad \rightarrow \ \ \quad -7x^3 \quad + \ \ \quad 3x^2 \quad + \quad -x \quad + \quad \quad 4 \quad \ \\ & \underline{\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; -(-6x^2+9) \quad \rightarrow \quad \quad \quad \quad \quad \quad \quad \ \ 6x^2 \qquad \qquad \qquad \qquad -9 \ \; \; \; \; \; \;} \end{align*}$
:-7x3+3x2-x+4)--7x3+3x2xx4-(-6x2+9)-6x2-9_

Next, combine like terms.
::接下来,把术语合并起来。


$\begin{aligned} (- 7 x^{3} + 3 x^{2} - x + 4) \to - 7 x^{3} + 3 x^{2} + - x + 4 \\ \underline{- (- 6 x^{2} + 9) \to 6 x^{2} - 9} \\ - 7 x^{3} + 9 x^{2} - x - 5 \leftarrow - 7 x^{3} + 9 x^{2} + - x + - 5 \end{aligned}$
$\begin{align*}& \quad (-7x^3+3x^2-x+4) \quad \rightarrow \ \ \quad -7x^3 \quad + \ \ \quad 3x^2 \quad + \quad -x \quad + \quad \quad 4 \quad \ \\ & \underline{\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; -(-6x^2+9) \quad \rightarrow \quad \quad \quad \quad \quad \quad \quad \ \ 6x^2 \qquad \qquad \qquad \qquad -9 \ \; \; \; \; \; \;} \\ & \quad -7x^3+9x^2-x-5 \quad \ \leftarrow \quad \quad -7x^3 \quad + \quad \ 9x^2 \quad + \quad -x \quad + \quad -5 \quad \ \end{align*}$
:-7x3+3x2+3x2-x+4)--7x3+3x2*x+4-(-6x2+9)--(-6x2+9)-)-6x2-9 *7x3+9x2-x2-x5 *7x3+9x2x2-5)

The answer is $\begin{align*}-7x^3 + 9x^2 - x -5\end{align*}$ .
::答案是- 7x3+9x2- x-5 。

Example 3
::例3

Subtract the polynomials: $\begin{align*}(8x^2 + 4x- 7) - (2x^2 + 9x + 3)\end{align*}$ .
::减号数: (8x2+4x-7) - (2x2+9x+3)

First, rewrite the polynomials without parentheses. Remember that subtracting is adding the opposite.
::首先, 在没有括号的情况下重写多面体。记住减法是增加反面的。

$\begin{aligned} (8 x^{2} + 4 x - 7) - (2 x^{2} + 9 x + 3) = 8 x^{2} + 4 x - 7 - 2 x^{2} - 9 x - 3 \end{aligned}$
$\begin{align*}(8x^2 + 4x - 7) - (2x^2 + 9x + 3) = 8x^2 + 4x -7 - 2x^2 - 9x - 3 \end{align*}$
:8x2+4x-7)-(2x2+9x+3)=8x2+4x-7-2x2-9x-3

Next, combine like terms.
::接下来,把术语合并起来。


$\begin{aligned} \begin{array}{rcl} (8 x^{2} + 4 x - 7) - (2 x^{2} + 9 x + 3) & = & 8 x^{2} + 4 x - 7 - 2 x^{2} - 9 x - 3 \\ = & 6 x^{2} - 5 x - 10 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (8x^2 + 4x - 7) - (2x^2 + 9x + 3) &=& {\color{blue}8x^2} + {\color{red}4x} -7 {\color{blue} - 2x^2} {\color{red} - 9x} - 3 \\ &=& 6{\color{blue}x^2} - {\color{red}5x} - 10 \end{array}\end{align*}$

The answer is $\begin{align*}6x^2 - 5x - 10\end{align*}$ .
:8x2+4x-7)-(2x2+9x+3)=8x2+4x-7-2x2-9x3=6x2-5x-10) 答案是 6x2-5x-10。

Example 4
::例4

Subtract the polynomials: $\begin{align*}(10xy + 4x- 7) - (3x- 4)\end{align*}$ .
::乘以多数值: (10xy+4x-7)-(3x-4)-(3x-4)。

First, rewrite the polynomials without parentheses. Remember that subtracting is adding the opposite.
::首先, 在没有括号的情况下重写多面体。记住减法是增加反面的。

$\begin{aligned} (10 x y + 4 x - 7) - (3 x - 4) = 10 x y + 4 x - 7 - 3 x + 4 \end{aligned}$
$\begin{align*}(10xy + 4x - 7) - (3x - 4) = 10xy + 4x - 7 - 3x + 4\end{align*}$
:10xy+4x-7)-(3x-4)=10xy+4x-7-3x+4

Next, combine like terms.
::接下来,把术语合并起来。

$\begin{aligned} \begin{array}{rcl} (10 x y + 4 x - 7) - (3 x - 4) & = & 10 x y + 4 x - 7 - 3 x + 4 \\ = & 10 x y + x - 3 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (10xy + 4x - 7) - (3x - 4) &=& 10xy + {\color{red}4x} {\color{blue}- 7} {\color{red}- 3x} + {\color{blue}4} \\ &=& 10xy + {\color{red}x} {\color{blue} -3} \end{array}\end{align*}$
:10xy+4x-7)-(3x-4)=10xy+4x-7-3x+4=10xy+3)

The answer is $\begin{align*}10xy + x - 3\end{align*}$ .
::答案是 10xy+x-3。

Example 5
::例5

Subtract the polynomials: $\begin{align*}(14x^2 + 8x- 7y + 1) - (2x^2 + 2x- 4y + 2)\end{align*}$ .
::减乘多数值14x2+8x-7y+1)-(2x2+2x-4y+2)。

First, rewrite the polynomials without parentheses. Remember that subtracting is adding the opposite.
::首先, 在没有括号的情况下重写多面体。记住减法是增加反面的。

$\begin{aligned} (14 x^{2} + 8 x - 7 y + 1) - (2 x^{2} + 2 x - 4 y + 2) = 14 x^{2} + 8 x - 7 y + 1 - 2 x^{2} - 2 x + 4 y - 2 \end{aligned}$
$\begin{align*}(14x^2 + 8x - 7y + 1) - (2x^2 + 2x -4y + 2) = 14x^2 + 8x - 7y + 1 - 2x^2 -2x + 4y - 2\end{align*}$

:14x2+8x-7y+1)-(2x2+2x-4y+2)=14x2+8x-7y+1-2x2-2x+4y-2)

Next, combine like terms.
::接下来,把术语合并起来。

$\begin{aligned} \begin{array}{rcl} (14 x^{2} + 8 x - 7 y + 1) - (2 x^{2} + 2 x - 4 y + 2) & = & 14 x^{2} + 8 x - 7 y + 1 - 2 x^{2} - 2 x + 4 y - 2 \\ = & 12 x^{2} + 6 x - 3 y - 1 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (14x^2 + 8x - 7y + 1) - (2x^2 + 2x -4y + 2) &=& {\color{purple}14x^2} + {\color{red}8x} {\color{blue}- 7y} + 1 {\color{purple}- 2x^2} {\color{red} -2x} + {\color{blue}4y} - 2 \\ &=& {\color{purple}12x^2} + {\color{red}6x} {\color{blue}-3y} - 1 \end{array}\end{align*}$
:14x2+8x-7y+1)-(2x2+2x-2x-4y+2)=14x2+8x-7y+1-2x2-2x-2x+4y-2=12x2+6x-3y-1)

The answer is $\begin{align*}12x^2 + 6x - 3y - 1\end{align*}$ .
::答案是 12x2+6x-3y-1。

Review
::回顾

Subtract the following polynomials vertically.
::垂直减减以下多数值。

1. $\begin{align*}(6x^2 + 5x) - (3x^2 - 14x + 2)\end{align*}$
::1. (6x2+5x)-(3x2-14x+2)

2. $\begin{align*}(3x^2 + 5x + 3) - (2x^2 - x + 4)\end{align*}$
::2. (3x2+5x+3)-(2x2-x+4)

3. $\begin{align*}(5xy + 5x + 3) - (12xy - 4x - 8)\end{align*}$
::3. (5xy+5x+3)-(12xy-4x-8)

4. $\begin{align*} (5y^2 + 5y - 2) - (3y^2 - 6y + 5)\end{align*}$
::4. (5y2+5y-2)-(3y2-6y+5)

5. $\begin{align*}(8x + 5y + 1) - (9x + 2y + 5)\end{align*}$
::5. (8x+5y+1)-(9x+2y+5)

6. $\begin{align*}(7x^2 + x - 3) - (3x^2 + 3x + 4)\end{align*}$
::6. (7x2+x-3)-(3x2+3x+4)

7. $\begin{align*} (8x + 5y + 4) - (3x - 9y + 4)\end{align*}$
::7. (8x+5y+4)-(3x-9y+4)

8. $\begin{align*}(18x^3 + 2x^2 + 8x + 2) - (3x^2 - 4x - 9)\end{align*}$
::8. (18x3+2x2+8x+2)-(3x2-4x-9)

9. $\begin{align*}(8x + 9y - 20) - (3x - 14)\end{align*}$
::9. (8x+9y-20)-(3x-14)

10. $\begin{align*}(16x^2 + 5x - 3y + 7) - (3x - 14y + 10)\end{align*}$
::10. (16x2+5x-3y+7)-(3x-14y+10)

11. $\begin{align*}(18x^2 + 5xy - 6x + 21) - (3x^2 - 14xy - 9x + 1)\end{align*}$
::11. (18x2+5xy-6xx+21)-(3x2-14xy-9x+1)

12. $\begin{align*}(7y^3 + 4y^2 - 3y - 1) - (y^3 + 6y^2 - 4)\end{align*}$
::12. (7y3+4y2-3y-1)-(y3+6y2-4)

Subtract the following polynomials horizontally.
::水平减以下列多元数值。

13. $\begin{align*}(m^2 + 17m - 11) - (3m^2 + 8m + 12)\end{align*}$
::13. (m2+17m-11)-(3m2+8m+12)

14. $\begin{align*}(z^2 + 3z) - (3z^2 + 7z + 16) - (4z - 13)\end{align*}$
::14. (z2+3z)-(3z2+7z+16)-(4z-13)

15. $\begin{align*}(5x^2 + 3xy) - (3x^2 + 7xy + 16) - (4xy - 13)\end{align*}$
::15. (5x2+3xy)-(3x2+7xy+16)-(4xy-13)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

减 减 多元数

Subtracting Polynomials ::减 减 多元数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

减减多元数

Subtracting Polynomials
::减减多元数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)