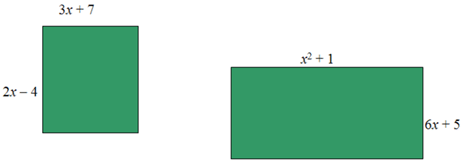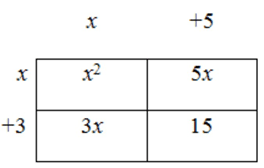12.11 倍比义体

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 乘数分义

  Collapse Expand

  乘数分义

  

  Brenda and her mother are walking through their local community garden, enjoying the gentle aromas and beautiful colors on display. While her mother talks to one of the gardeners, Brenda looks through the brochure with all the garden dimensions and comes up with a math challenge for her mother:

  播放段落

  If one field dedicated to vegetables measures $\begin{align*}3x + 7 \end{align*}$  by $\begin{align*}2x - 4\end{align*}$ , while another field dedicated to flowers measures $\begin{align*}x^2 + 1\end{align*}$  by $\begin{align*}6x + 5\end{align*}$ , what is the combined area of the two fields?
  ::如果一个专门用于蔬菜的字段用3x+7乘2x-4计量3x+7乘2x-4,而另一个专门用于花朵的字段用x2+1乘6x+5计量x2+1乘6x+5,这两个字段的合并区域是什么?

  播放段落

  

  
  
  In this concept, you will learn to multiply binomials vertically , horizontally and by using a table.
  ::在此概念中,您将学会垂直、横向和通过使用表格来增加二进制。

  播放段落

  Multiplying Binomials
  ::乘数分义

  播放段落

  Binomials are defined as two- term . When you add and subtract polynomials, you are careful to combine like terms . When you multiply polynomials you will carefully apply the rules of exponents, as well.
  ::二进制定义为两期。当您加和减多式数字时,要小心将类似术语合并。当您乘多式数字时,也要小心地应用引言人的规则。

  播放段落

  When you multiply binomials, you can use a table to help us to organize and keep track of the information.
  ::当您乘以二进制时, 您可以使用一个表格来帮助我们组织和跟踪信息 。

  播放段落

  Let’s look at an example.
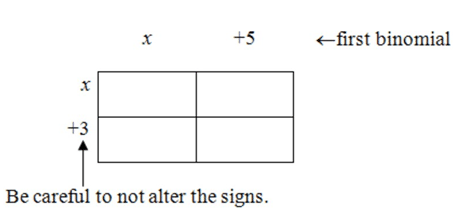
  ::让我们举个例子。

  播放段落

  Multiply the binomials  $\begin{align*}(x + 5)(x + 3)\end{align*}$ .
  ::乘以二进制 (x+5)(x+3) 。

  播放段落

  First, use a table like a rectangle, as if each of the binomials were a dimension of the rectangle. You will insert the two binomials along the sides of the table like a rectangle.
  ::首先,像矩形一样使用一张桌子, 好像每个二进制是矩形的一个维度。 您可以像一个矩形一样在桌子两边插入两个二进制。

  

  播放段落

  Next, find the area of the four separate rectangles.
  ::接下来,找到四个独立的矩形区域。

  

  播放段落

  The dimensions of the first rectangle are  $\begin{align*}x \times x\end{align*}$ , while dimensions of the second are  $\begin{align*}5 \times x\end{align*}$ , the third are  $\begin{align*}3 \times x\end{align*}$ , and the fourth are  $\begin{align*}3 \times 5\end{align*}$ .
  ::第一个矩形的尺寸是xxxx,第二个的尺寸是5xxx,第三个是3xx,第四个是3x5。

  播放段落

  Then, in order to find the total, you will add the four areas and combine like terms.
  ::然后,为了找到总数,你将增加四个区域,并合并类似术语。

  播放段落

  $$\begin{align*}\begin{array}{rcl} && x^2 + 5x + 3x + 15 \\ && x^2 + 8x + 15 \end{array}\end{align*}$$
  ::x2+5x+3x+15x2+8x+15

  播放段落

  The answer is $\begin{align*}x^2 + 8x + 15\end{align*}$ .
  ::答案是 x2+8x+15 。

  播放段落

  Here is an example that is a little different.
  ::这里的例子稍有不同。

  播放段落

  Multiply $\begin{align*}(5x - 8)^2\end{align*}$ .
  ::乘以 (5x-8) 2。

  播放段落

  First, remember that the exponent applies to the entire binomial such that
  ::首先,请记住,前言适用于整个二元论,因此:

  播放段落

  $$\begin{align*}(5x - 8)^2 = (5x - 8)(5x - 8)\end{align*}$$
  :5x-8)2=(5x-8)5x-8)

  播放段落

  Fill in the table below with the areas of each of the rectangles.
  
  

  

  
  ::在下表中填充每个矩形的面积。

  播放段落

  Next, in order to find the total, you will add the four areas and combine like terms.
  ::接下来,为了找到总计,你将添加四个区域,并合并类似术语。

  播放段落

  $$\begin{align*}\begin{array}{rcl} && 25x^2 - 40x - 40x + 64 \\ && 25x^2 - 80x + 64 \end{array}\end{align*}$$
  ::25x2-40x-40x-40x+6425x2-80x+64

  播放段落

  The answer is $\begin{align*}25x^2 - 80x + 64\end{align*}$ .
  ::答案是 25x2-80x+64。

  播放段落

  A second method for multiplying binomials is similar to the algorithm commonly used for multiplying two- digit numbers. You can multiply binomials vertically in the same manner.
  ::计算二进制的第二个方法与计算两位数时常用的算法相似。您可以以同样的方式垂直计算二进制。

  播放段落

  Let’s take a look at an example.
  ::让我们举个例子。

  播放段落

  Multiply:
  ::乘数 :

  播放段落

  $$\begin{align*}(3x + 2)(5x + 4)\end{align*}$$
  :3x+2)(5x+4)

  播放段落

  First, set up the vertical multiplication . 
  ::首先,设置垂直乘法。

  播放段落

  $$\begin{align*}& 2^{nd} \ \text{power} \qquad \ \quad 1^{st} \ \text{power} \qquad \quad 0 \ \text{power} \\ & \qquad \qquad \qquad \qquad \ \ \ \quad 3x \quad \ + \qquad \quad 2 \\ & \underline{ \times \qquad \quad \qquad \qquad \qquad 5x \quad \ + \quad \qquad 4 \;\;\;\;\;\;\;} \\\end{align*}$$
  ::二号电源 1号电源 3x +2x5x +4_

  播放段落

  Next, complete the vertical multiplication.
  ::下一步,完成垂直乘法。

  播放段落

   

  $$\begin{align*}& 2^{nd} \ \text{power} \qquad \ \quad 1^{st} \ \text{power} \qquad \quad 0 \ \text{power} \\ & \qquad \qquad \qquad \qquad \ \ \ \quad \ 3x \quad + \qquad \ \quad 2 \\ & \underline{\qquad \qquad \qquad \qquad \qquad 5x \quad + \qquad \ \quad 4 \;\;\;\;\;} \\ & \qquad \qquad \qquad \qquad \ \ \quad 12x \quad + \qquad \ \quad 8 \\ & \underline{\qquad 15x^2 \quad + \qquad \ \ \quad 10x \ \quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ & \qquad 15x^2 \quad + \qquad \ \ \quad 22x \ \ \ + \qquad \ \ \quad 8\end{align*}$$
  ::第二电源一号电源 3x+ 25x+ 4_ 12x+ 12x+ 815x2+ 10x_15x2+ 22x+8

  播放段落

  The answer is $\begin{align*}15x^2 + 22x +8\end{align*}$ .
  ::答案是 15x2+22x+8。

  播放段落

  A third way is to use “ FOIL ”. FOIL is an acronym which tells you which terms to multiply in order to get the product of the two binomials.
  ::第三种方式是使用“FOIL”,FOIL是一个缩略语,缩略语表示为了获得两个二元体的产物,要乘用哪个术语。

  播放段落

  FOIL stands for:
  ::FOIL代表:

  播放段落

  F: First terms in the binomials
  ::F:二进制的第一个术语

  播放段落

  O: Outside terms in the binomials
  ::O:二进制中的外部术语

  播放段落

  I: Inside terms in the binomials
  ::一:二进制的内在术语

  播放段落

  L: Last terms in the binomials
  ::L:二进制最后术语

  播放段落

  Let’s look at an example.
  ::让我们举个例子。

  播放段落

  Multiply using the FOIL method.
  ::使用FOIL方法乘法 。

  播放段落

  $$\begin{align*}(2x + 8)(5x - 13)\end{align*}$$
  :2x+8)(5x-13)

  播放段落

  First, multiply the first two terms.
  ::首先,乘以前两个条件。

  播放段落

  $$\begin{align*}({\color{red} 2x} + 8) ({\color{red}5x} - 13)\end{align*}$$
  :2x+8)(5x-13)

  播放段落

  First terms:  $\begin{align*}2x \times 5x = 10x^2\end{align*}$
  ::第一术语: 2xxx5x=10x2

  播放段落

  Next, multiply the outside terms.
  ::接下来,乘以外部条件。

  播放段落

   

  $$\begin{align*}({\color{red} 2x} + 8) (5x{\color{red}-13)}\end{align*}$$
  :2x+8)(5x-13)

  播放段落

  Outside terms:  $\begin{align*}2x \times - 13 = -26x\end{align*}$
  ::外语: 2x1326x

  播放段落

  Next, multiply the inside terms.
  ::下一个,乘以内部术语。

  播放段落

  $$\begin{align*}(2x + {\color{red}8}) ({\color{red}5x} -13)\end{align*}$$
  :2x+8)(5x-13)

  播放段落

  Inside terms:  $\begin{align*}8 \times 5x = 40x\end{align*}$
  ::内含术语: 8x5x=40x

  播放段落

  Then, multiply the last two terms. 

  $$\begin{align*}(2x + {\color{red}8}) (5x{\color{red}-13})\end{align*}$$
  ::然后乘以最后两个条件。 (2x+8) (5x-13)

  播放段落

  Last terms:  $\begin{align*}8 \times - 13 = -104\end{align*}$
  ::任期:最后任期: 813104

  播放段落

  Then, combine like terms.
  ::然后,合并起来像术语一样。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (2x + 8)(5x - 13) &=& 10x^2 - 26x + 40x - 104 \\ &=& 10x^2 + 14x - 104 \end{array}\end{align*}$$
  :2x+8)(5x-13)=10x2-26x+40x-104=10x2+14x-104)

  播放段落

  The answer is $\begin{align*}10x^2 + 14x - 104\end{align*}$ .
  ::答案是 10x2+14x-104。

  播放段落

  Of the three methods in this concept for multiplication, you might agree that this is the quickest method. Of course, all three methods would give you the same product.
  ::在这个乘法概念中的三种方法中,你可能会同意这是最快的方法。 当然,所有三种方法都会给你同样的产品。

  播放段落

  Take a look at one more.
  ::再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼,再看一眼。

  播放段落

  Multiply using the FOIL method.
  ::使用FOIL方法乘法 。

  播放段落

  $$\begin{align*}(5x^3 + 2x)(7x^2 + 8)\end{align*}$$
  :5x3+2x)(7x2+8)

  播放段落

  First, use FOIL to find the four terms that result from multiplying the two binomials.
  ::首先,使用FOIL 来找到乘以两个二元论 得出的四个条件。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (5x^3 + 2x)(7x^2 + 8) &=& 5x^3 \times 7x^2 + 5x^3 \times 8 + 2x \times 7x^2 + 2x \times 8 \\ &=& 35x^5 + 40x^3 + 14x^3 + 16x \end{array}\end{align*}$$
  :5x3+2x)(7x2+8)=5x3x7x2+5x3x3x8+2x7x2+2xx8=35x5+40x3+14x3+16xx

  播放段落

  Next, combine like terms.
  ::接下来,把术语合并起来。

  播放段落

  $$\begin{align*}35x^5 + 40x^3 + 14x^3 + 16x = 35x^5 + 54x^3 + 16x\end{align*}$$
  ::35x5+40x3+14x3+16x=35x5+54x3+16x

  播放段落

  The answer is $\begin{align*}35x^5 + 54x^3 + 16x\end{align*}$ .
  ::答案是 35x5+54x3+16x。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  
  Earlier, you were given a problem about  Brenda’s math challenge for her mother.
  ::Brenda对母亲的数学挑战,

  播放段落

  Brenda ends up helping her mother work out the area of both rectangles and then the sum of those two areas to get the total area.
  ::布伦达最终帮助她的母亲 解决了两个矩形区域的问题 然后这两个区域的总和 才能得到全部区域

  播放段落

  First, they find the area of the first rectangle using FOIL.
  ::首先,他们利用FOIL找到第一个矩形区域。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (3x +7)(2x - 4) &=& 3x \times 2x + 3x \times -4 + 7 \times 2x + 7 \times -4 \\ &=& 6x^2 - 12x + 14x - 28 \\ &=& 6x^2 + 2x - 28 \end{array}\end{align*}$$
  :3x+7)(2x-4)=3xx2x+3x=4+7x2x+7*4=6x2-12x+14x-28=6x2+2x-28)

  播放段落

  Next, they find the area of the second rectangle using FOIL.
  ::接下来,他们用FOIL找到第二个矩形的区域。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (x^2 + 1)(6x + 5) &=& x^2 \times 6x + x^2 \times 5 + 1 \times 6x + 1 \times 5 \\ &=& 6x^3 + 5x^2 + 6x + 5 \end{array}\end{align*}$$
  :x2+1)(6x+5) =x2x6x+x2x5+1x6x1x5=6x3+5x2+6x5)

  播放段落

  Then, they add the two areas together to find the total area.
  ::然后,他们将这两个区域加在一起,以找到总面积。

  播放段落

  $$\begin{align*}\begin{array}{rcl} \text{Total Area} &=& (6x^2 + 2x - 28) +(6x^3 + 5x^2 + 6x + 5) \\ &=& 6x^3 + 11x^2 + 8x - 23 \end{array}\end{align*}$$
  ::总面积=(6x2+2x-28)+(6x3+5x2+6x5)=6x3+11x2+8x-23

  播放段落

  The answer is $\begin{align*}6x^3 + 11x^2 + 8x - 23\end{align*}$ .
  ::答案是 6x3+11x2+8x-23。

  播放段落

  Example 2
  ::例2

  播放段落

  Multiply by using a table.
  ::使用表格乘以 。

  播放段落

   

  $$\begin{align*}(x - 4)(x - 6)\end{align*}$$
  :x-4(x-6))

  播放段落

  First, fill in the table below with the areas of each of the rectangles.
  ::首先,在下表中填写每个矩形的面积。

  

  播放段落

  Next, in order to find the total, you will add the four areas and combine like terms.
  ::接下来,为了找到总计,你将添加四个区域,并合并类似术语。

  播放段落

  $$\begin{align*}\begin{array}{rcl} && x^2 + 6x - 4x - 24 \\ && x^2 + 2x - 24 \end{array}\end{align*}$$
  ::x2+6x-4x-24x2+2x-24

  播放段落

  The answer is $\begin{align*}x^2 + 2x - 24\end{align*}$ .
  ::答案是 x2+2x-24 。

  播放段落

  Example 3
  ::例3

  播放段落

  Multiply  $\begin{align*}(x + 2)(x + 4)\end{align*}$ .
  ::乘号 (x+2)(x+4) 。

  播放段落

  First, fill in the table below with the areas of each of the rectangles.
  ::首先,在下表中填写每个矩形的面积。

  

  播放段落

  Next, in order to find the total, you will add the four areas and combine like terms.
  ::接下来,为了找到总计,你将添加四个区域,并合并类似术语。

  播放段落

  $$\begin{align*}& x^2 + 4x + 2x + 8 \\ & x^2 + 6x + 8\end{align*}$$
  
  The answer is $\begin{align*}x^2 + 6x + 8\end{align*}$ .
  ::x2+4x+2x+8x2+6x+8 答案为 x2+6x+8。

  播放段落

  Example 4
  ::例4

  播放段落

  Multiply  $\begin{align*}(x-6)(x+5)\end{align*}$ .
  ::乘(x-6)(x+5)。

  播放段落

  First, use FOIL to find the four terms that result from multiplying the two binomials.
  ::首先,使用FOIL 来找到乘以两个二元论 得出的四个条件。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (x - 6)(x + 5) &=& x \times x + x \times 5 - 6 \times x - 6 \times 5 \\ &=& x^2 + 5x -6x - 30 \end{array}\end{align*}$$ Next, combine like terms.
  :x-6)(x+5)=xx+xxxxxxxxxxxxxx5-6xxx-6x5=x2+5x-6x-30Next),将类似术语合并。

  播放段落

  $$\begin{align*}x^2 + 5x -6x - 30 = x^2 - x - 30\end{align*}$$
  ::x2+5x-6x-30=x2-x-30

  播放段落

  The answer is $\begin{align*}x^2 - x - 30\end{align*}$ .
  ::答案是 x2 -x -30 。

  播放段落

  Example 5
  ::例5

  播放段落

  Multiply $\begin{align*}(x-3)(x+3)\end{align*}$ .
  ::乘(x-3)(x+3)。

  播放段落

  First, use FOIL to find the four terms that result from multiplying the two binomials.
  ::首先,使用FOIL 来找到乘以两个二元论 得出的四个条件。

  播放段落

  $$\begin{align*}\begin{array}{rcl} (x - 3)(x + 3) &=& x \times x + x \times 3 - 3 \times x - 3 \times 3 \\ &=& x^2 + 3x - 3x - 9 \end{array}\end{align*}$$
  Next, combine like terms.
  :x-3 (x+3) =xxx+xxx-3-3x-3x-3x-3x-3x-3x3=x2+3x-3x-3x-9) 下一步,将类似术语合并。

  播放段落

  $$\begin{align*}x^2 + 3x - 3x - 9 = x^2 - 9\end{align*}$$
  ::x2+3x-3x-9=x2-9

  播放段落

  The answer is $\begin{align*}x^2 - 9\end{align*}$ .
  ::答案是 x2- 9 。

  播放段落

  Review
  ::回顾

  播放段落

  Use a table to multiply the following binomials.
  ::使用表格乘以以下二进制。

  播放段落

  1.  $\begin{align*}(x + 3)(x + 5)\end{align*}$
  ::1. (x+3)(x+5)

  播放段落

  2.  $\begin{align*}(x - 3)(x - 5)\end{align*}$
  ::2. (x-3)(x-5)

  播放段落

  3.  $\begin{align*}(x + 3)(x - 3)\end{align*}$
  ::3. (x+3)(x-3)

  播放段落

  4.  $\begin{align*}(x + 2)(x - 8)\end{align*}$
  ::4. (x+2)(x-8)

  播放段落

  5.  $\begin{align*}(3x^2 + 3x)(6x - 2) \end{align*}$
  ::5. (3x2+3x(6x-2))

  播放段落

  6.  $\begin{align*}(2x - 7y)(5x + 4y)\end{align*}$
  ::6. (2x-7y)(5x+4y)

  播放段落

  7.  $\begin{align*}(2x - 9)^2\end{align*}$
  ::7. (2x-9)2

  播放段落

  Multiply the following binomials vertically.
  ::垂直乘以以下二进制。

  播放段落

  8.  $\begin{align*}(d + 2)(4d - 1)\end{align*}$
  ::8. (d+2)(4d-1)

  播放段落

  9.  $\begin{align*}(5x + 7)(5x - 7)\end{align*}$  
  ::9. (5x+7)(5x-7)

  播放段落

  10.  $\begin{align*}(4b^2 + 3c)(2b - 5c^2)\end{align*}$
  ::10. (4b2+3c)(2b-5c2)

  播放段落

  Multiply the following binomials using the FOIL method.
  ::使用FOIL方法乘以以下二进制。

  播放段落

  11.  $\begin{align*}(p + 6)(5p + 2) \end{align*}$
  ::11. (p+6)(5p+2)

  播放段落

  12.  $\begin{align*}(-7y^2 - 4y)(6y + 2)\end{align*}$
  ::12. (-7y2-4y)(6y+2)

  播放段落

  13.  $\begin{align*}(x^3 + 3x)^2\end{align*}$
  ::13. (x3+3x)2

  播放段落

  14.  $\begin{align*}(2x + 1)(x - 4)\end{align*}$
  ::14. (2x+1)(x-4)

  播放段落

  15.  $\begin{align*} (3x - 3) (5x + 9)\end{align*}$
  ::15. (3x-3(5x+9))

  播放段落

  16.  $\begin{align*} (x + 5)^2\end{align*}$
  ::16. (x+5)2

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

   

  播放段落

  Resources
  ::资源