1.1 基本几何定义

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 基本几何基本定义

  Collapse Expand

  基本几何基本定义

  播放段落

  Geometric Definitions
  ::几何定义

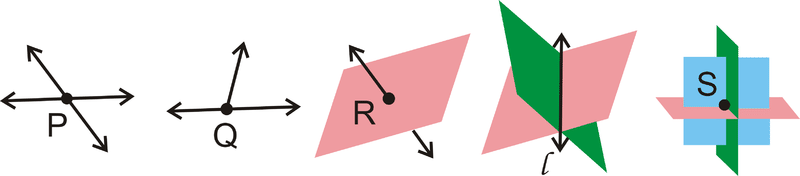
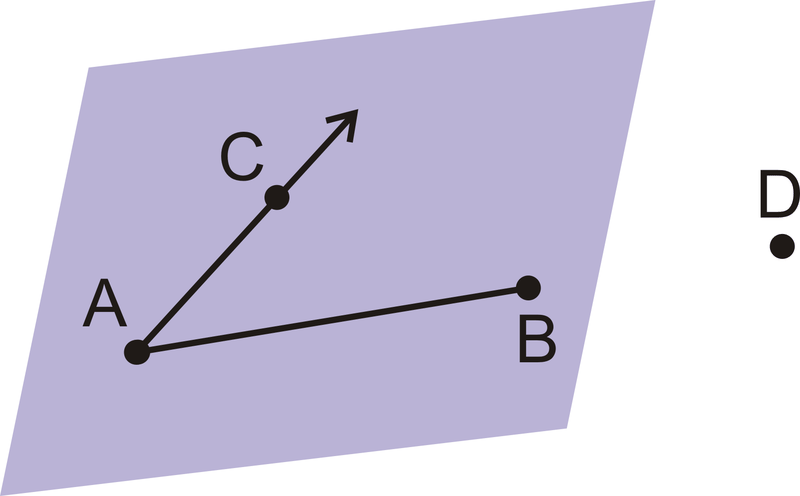
  播放段落

  A point is an exact location in space . It describes a location, but has no size. Examples are shown below:
  ::点是空间中的确切位置。它描述一个位置,但没有大小。示例如下:

  

  Label It	Say It
  $\begin{align*}A\end{align*}$	point $\begin{align*}A\end{align*}$

  播放段落

  A line is infinitely many points that extend forever in both directions. Lines have direction and location and are always straight .
  ::一条线是无限多的点,在两个方向上永远延伸。 一条线有方向和位置,并且总是直的。

  

  Label It	Say It
  line $\begin{align*}g\end{align*}$	line $\begin{align*}g\end{align*}$
  $\begin{align*}\overleftrightarrow{\text{PQ}}\end{align*}$	line $\begin{align*}PQ\end{align*}$

  播放段落

  A plane is a flat surface that contains infinitely many intersecting lines that extend forever in all directions. Think of a plane as a huge sheet of paper with no thickness that goes on forever.
  ::平面是一个平面, 包含无限多的交叉线, 在所有方向都永久延伸。 将平面想象成一张巨大的纸, 没有永久的厚度 。

  

  Label It	Say It
  Plane $\begin{align*}\mathcal{M}\end{align*}$	Plane $\begin{align*}M\end{align*}$
  Plane $\begin{align*}ABC\end{align*}$	Plane $\begin{align*}ABC\end{align*}$

  播放段落

  We can use point , line , and plane to define new terms.
  ::我们可以用点、线和平面来定义新的术语。

  播放段落

  Space is the set of all points extending in three dimensions . Think back to the plane. It extended in two dimensions, what we think of as up/down and left/right. If we add a third dimension, one that is perpendicular to the other two, we arrive at three-dimensional space.
  ::空间是三个维度中所有点的一组。 回想到平面中。 它在两个维度中延伸, 我们称之为向上/ 向下和向左/ 向右。 如果我们加上第三个维度, 一个与其它两个维度垂直, 我们到达三维空间 。

  播放段落

  Points that lie on the same line are collinear . $\begin{align*}P, Q, R, S,\end{align*}$  and $\begin{align*}T\end{align*}$ are collinear because they are all on line $\begin{align*}w.\end{align*}$  If a point $\begin{align*}U\end{align*}$ were located above or below line $\begin{align*}w,\end{align*}$  it would be non-collinear .
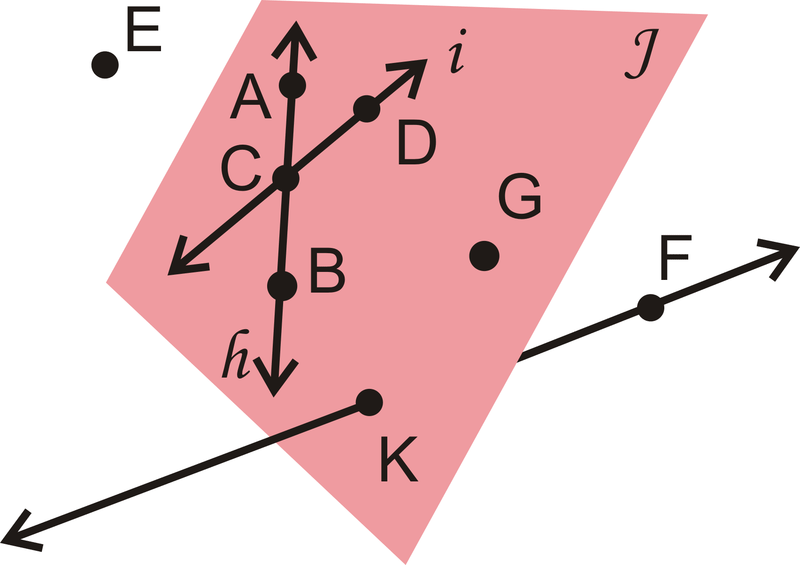
  ::同一线上的点是线性线性点。 P、 Q、 R、 S 和 T 是线性点, 因为它们都是线性点。 如果U点位于线上或线下, 它将是非线性点 。

  

  播放段落

  Points and/or lines within the same plane are coplanar . Lines $\begin{align*}h\end{align*}$ and $\begin{align*}i,\end{align*}$ and points $\begin{align*}A, B, C, D, G,\end{align*}$  and $\begin{align*}K\end{align*}$ are coplanar in Plane $\begin{align*}\mathcal{J}.\end{align*}$  Line $\begin{align*}\overleftrightarrow{KF}\end{align*}$ and point $\begin{align*}E\end{align*}$ are non-coplanar with Plane $\begin{align*}\mathcal{J}.\end{align*}$
  ::同一平面内的点和/或线系为共平面。 h线和i线,A线、B线、C线、D线、G线和K线系在Plane J线上的点和/或线系为共平面。

  

  播放段落

  An endpoint is a point at the end of a line segment . A line segment is a portion of a line with two endpoints. Or, it is a finite part of a line that stops at both ends. Line segments are labeled by their endpoints. Order does not matter.
  ::端点是线段结尾的点。线段是两个端点的线条的一部分。或者,是两端都停的线条的有限部分。线段按其端点贴上标签。顺序无关紧要。

  

  Label It	Say It
  $\begin{align*}\overline{AB}\end{align*}$	Segment $\begin{align*}AB\end{align*}$
  $\begin{align*}\overline{BA}\end{align*}$	Segment $\begin{align*}BA\end{align*}$

  播放段落

  A ray  is a part of a line. It begins with an endpoint and extends forever away from the endpoint in one direction, perfectly straight. A ray is labeled by its endpoint and one other point on the ray. For rays, order does matter. When labeling, put the endpoint under the side WITHOUT the arrow.
  ::光线是线条的一部分。 它从端点开始, 并且永远从端点向一个方向延伸, 完全直线。 光线用端点和射线上的另一点贴上标签。 对于射线, 命令很重要 。 在标签时, 将端点置于侧面下, 不使用箭头 。

  

  Label It	Say It
  $\begin{align*}\overrightarrow{CD}\end{align*}$	Ray $\begin{align*}CD\end{align*}$
  $\begin{align*}\overleftarrow{DC}\end{align*}$	Ray $\begin{align*}CD\end{align*}$

  播放段落

  An intersection is a point or set of points where lines, planes, segments, or rays overlap.
  ::交叉点是指线条、平面、段或射线重叠的点或一组点。

  

  播放段落

  Postulates
  ::假设

  播放段落

  A postulate is a basic rule of geometry. Postulates are assumed to be true (rather than proven), much like definitions. The following is a list of some basic postulates.
  ::假设是几何学的基本规则。 假设假设是真实的( 而不是经过验证的 ) , 非常相似的定义 。 以下列出一些基本假设 。

  播放段落

  Postulate #1: Given any two distinct points, there is exactly one (straight) line containing those two points.
  ::假设 # 1: 鉴于任何两个不同的点, 完全有一个包含这两个点的直线( 直线) 。

  

  播放段落

  Postulate #2: Given any three non-collinear points, there is exactly one plane containing those three points.
  ::假设2:鉴于任何三个非两极点, 精确地说有一架飞机含有这三个点。

  

  播放段落

  Postulate #3: If a line and a plane share two points, then the entire line lies within the plane.
  ::假设3:如果一线和一平面共有两点,则整线就位于该平面内。

  

  播放段落

  Postulate #4: If two distinct lines intersect, the intersection will be one point.
  ::4: 如果两条不同的线交叉, 十字路口将是一个点 。

  

  播放段落

  Lines $\begin{align*}l\end{align*}$ and $\begin{align*}m\end{align*}$ intersect at point $\begin{align*}A\end{align*}$ .
  ::A点的I线和m线交叉。

  播放段落

  Postulate #5: If two distinct planes intersect, the intersection will be a line.
  ::5: 如果两个不同的平面交叉, 十字路口将是一条线 。

  

  播放段落

  When making geometric drawings, be sure to be clear and label all points and lines.
  ::在绘制几何图画时,一定要清楚,标出所有点和线条。

  播放段落

  What if you were given a picture of a figure or object, like a map with cities and roads marked on it? How could you explain that picture geometrically? 
  ::如果有人给了你一张图象或物体的照片,比如一张有城市和道路标注的地图呢?你怎么用几何方式解释这个图象呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  What best describes San Diego, California on a globe: point, line, or plane?
  ::加州圣迭戈 球体上的最佳描述是什么: 点、线或飞机?

  播放段落

  A city is usually labeled with a dot, or point, on a globe.
  ::一个城市通常被贴上一个点或点的标签 在全球。

  播放段落

  Example 2
  ::例2

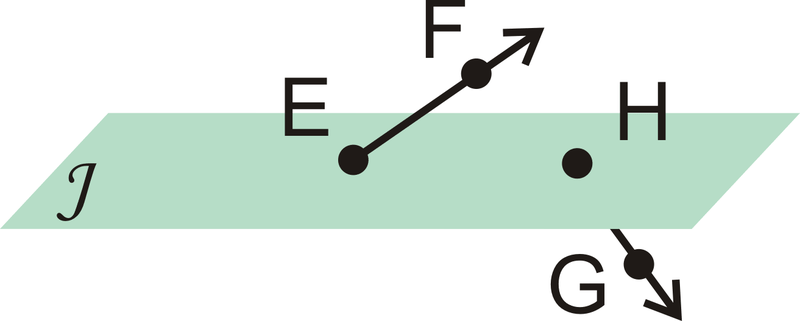
  播放段落

  Use the picture below to answer these questions.
  ::用下图解这些问题。

  

  播放段落
  1. List another way to label Plane $\begin{align*}\mathcal{J}\end{align*}$ .
     ::列出标签为 Plane J 的另一种方式 。

  播放段落

  Plane $\begin{align*}BDG\end{align*}$ is one possibility. Any combination of three coplanar points that are not collinear would be correct.
  ::3个非圆线共平板点的任何组合都是正确的。

  播放段落
  2. List another way to label line $\begin{align*}h\end{align*}$ .
     ::列出标签行 h 的另一种方式 。

  播放段落

  $\begin{align*}\overleftrightarrow{AB}\end{align*}$ . Any combination of two of the letters $\begin{align*}A, B\end{align*}$ , or $\begin{align*}C\end{align*}$ would also be correct.
  ::AB. 任何两个字母A、B或C的组合也是正确的。

  播放段落
  3. Are $\begin{align*}K\end{align*}$ and $\begin{align*}F\end{align*}$ collinear?
     ::K和F是山线吗?

  播放段落

  Yes, they both lie on $\begin{align*}\overleftrightarrow{KF}\end{align*}$ .
  ::是的,他们都躺在KF上

  播放段落
  4. Are $\begin{align*}E, B\end{align*}$ and $\begin{align*}F\end{align*}$ coplanar? 
     ::E,B和F是双平面吗?

  播放段落

  Yes, even though $\begin{align*}E\end{align*}$ is not in Plane $\begin{align*}\mathcal{J}\end{align*}$ , any three points make a distinct plane. Therefore, the three points create Plane $\begin{align*}EBF\end{align*}$ .
  ::是的,尽管E不是在Plane J中,但任何三点就是一个不同的平面。 因此,这三点就形成了Plane EBF。

  播放段落

  Example 3
  ::例3

  播放段落

  What best describes a straight road that begins in one city and stops in a second city: ray, line, segment, or plane?
  ::什么是最能描述一条直路,这条直路始于一个城市,在第二个城市停留:雷、线、线、段或飞机?

  播放段落

  The straight road connects two cities, which are like endpoints. The best term is segment.
  ::直路连接了两个城市,就像终点一样, 最好的用词是分路段。

  播放段落

  Example 4
  ::例4

  播放段落

  Answer the following questions about the picture.
  ::回答以下关于图片的问题。

  

  播放段落
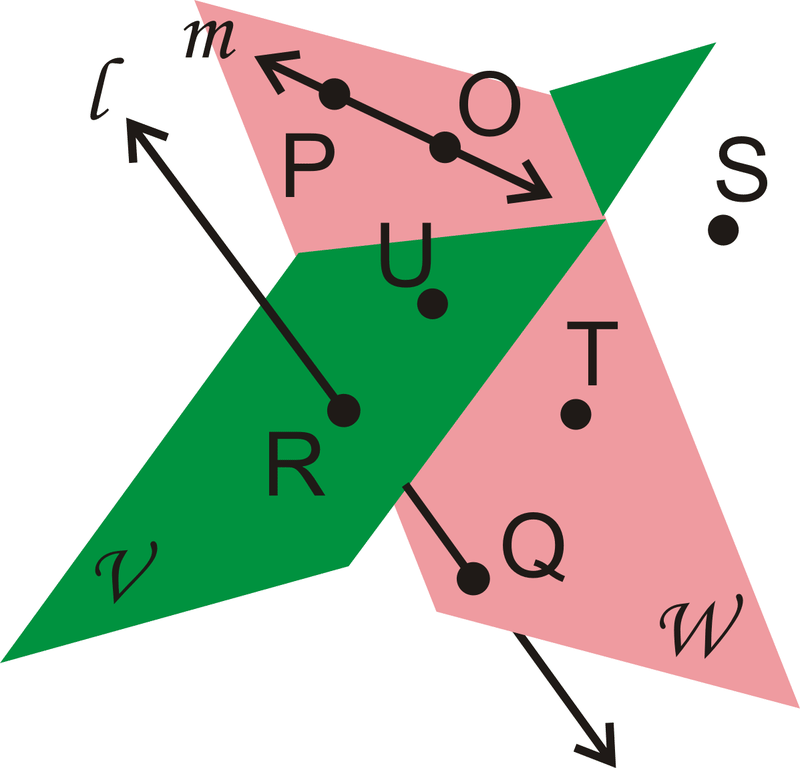
  1. Is line $\begin{align*}l\end{align*}$ coplanar with Plane $\begin{align*}\mathcal{V}\end{align*}$ , Plane $\begin{align*}\mathcal{W}\end{align*}$ , both, or neither? 
     ::L线与五号平面、W号平面或两者兼而有之吗?

  播放段落

  Neither
  ::中 无

  播放段落
  2. Are $\begin{align*}R\end{align*}$ and $\begin{align*}Q\end{align*}$ collinear? 
     ::R和Q是圆线吗?

  播放段落

  Yes
  ::是 是

  播放段落
  3. What point belongs to neither Plane $\begin{align*}\mathcal{V}\end{align*}$ nor Plane $\begin{align*}\mathcal{W}\end{align*}$ ? 
     ::第五号计划或W号计划都不属于哪个点?

  播放段落

  $\begin{align*}S\end{align*}$
  ::S S 级

  播放段落
  4. List three points in Plane $\begin{align*}\mathcal{W}\end{align*}$ . 
     ::W. Plane W.中列出三点。

  播放段落

  Any combination of $\begin{align*}P, O, T\end{align*}$ , and $\begin{align*}Q\end{align*}$ would work.
  ::任何P、O、T和Q的组合都会有效

  播放段落

  Example 5
  ::例5

  播放段落

  Draw and label a figure matching the following description: Line $\begin{align*}\overleftrightarrow{AB}\end{align*}$ and ray $\begin{align*}\overrightarrow{CD}\end{align*}$ intersect at point $\begin{align*}C\end{align*}$ . Then, redraw so that the figure looks different but is still true to the description.
  ::绘制并标签一个符合以下描述的图 : 线 AB 和 ray CD 在 C点交叉。 然后, 重新绘制, 使图看起来不同, 但仍符合描述 。

  播放段落

  Neither the position of $\begin{align*}A\end{align*}$ or $\begin{align*}B\end{align*}$ on the line, nor the direction that $\begin{align*}\overrightarrow{CD}\end{align*}$ points matter.
  ::无论是A或B在线上的位置,还是 " CD点点 " 的重要方向。

  

  播放段落

  For the second part, this is one way to draw the diagram differently:
  ::对于第二部分,这是以不同方式绘制图表的一种方法:

  

  播放段落

  Review
  ::回顾

  播放段落

  For questions 1-5, draw and label a figure to fit the descriptions.
  ::对于问题1至5,绘制和标出一个符合描述的数字。

  播放段落
  1. $\begin{align*}\overrightarrow{CD}\end{align*}$ intersecting $\begin{align*}\overleftrightarrow{AB}\end{align*}$ and Plane $\begin{align*}P\end{align*}$ containing $\begin{align*}\overleftrightarrow{AB}\end{align*}$ but not $\begin{align*}\overrightarrow{CD}\end{align*}$ .
     ::CD 交叉 AB 和 plane P , 包含 AB , 但不包含 CD 。
  播放段落
  2. Three collinear points $\begin{align*}A, B, \text{ and } C.\end{align*}$   $\begin{align*}B\end{align*}$ is also collinear with points $\begin{align*}D\end{align*}$ and $\begin{align*}E\end{align*}$ .
     ::A、B和C.B三个山丘线点也是D和E点的山丘线点。
  播放段落
  3. $\begin{align*}\overrightarrow{XY}, \ \overrightarrow{XZ},\end{align*}$  and $\begin{align*}\overrightarrow{XW},\end{align*}$ such that $\begin{align*}\overrightarrow{XY}\end{align*}$ and $\begin{align*}\overrightarrow{XZ}\end{align*}$ are coplanar, but $\begin{align*}\overrightarrow{XW}\end{align*}$ is non-coplanar with both of the other rays.
     ::XY, XZ, 和XW, 如此一来, XY 和XZ 是共平板, 但XW 与另外两种射线是非相平面的。
  播放段落
  4. Two intersecting planes, $\begin{align*}\mathcal{P}\end{align*}$ and $\begin{align*}\mathcal{Q}\end{align*}$ , with $\begin{align*}\overline{GH},\end{align*}$ where $\begin{align*}G\end{align*}$ is in plane $\begin{align*}\mathcal{P}\end{align*}$ and $\begin{align*}H\end{align*}$ is in plane $\begin{align*}\mathcal{Q}\end{align*}$ .
     ::两架交错的飞机,P和Q,G在G和H在G和Q之间。
  播放段落
  5. Four non-collinear points  $\begin{align*}I, J, K, \text{and }L,\end{align*}$  with line segments connecting all points to each other.
     ::4个非两极点I、J、K和L,各线段将所有点相互连接。
  播放段落
  6. Name this line in five ways.
     ::以五种方式命名此行 。
  播放段落
  7. Name the geometric figure in three different ways.
     ::以三种不同的方式列出几何数字。
  播放段落
  8. Name the geometric figure in two different ways.
     ::以两种不同的方式命名几何图。
  播放段落
  9. What is the best possible geometric model for a soccer field? Explain your answer.
     ::足球场的最佳几何模型是什么?
  播放段落
  10. List two examples of where you see rays in real life.
      ::列举两个例子, 说明您在现实生活中看到光线的地方 。
  播放段落
  11. What type of geometric object is the intersection of a line and a plane? Draw your answer.
      ::线和平面的交叉点是哪一类几何物体? 请绘制您的答案 。
  播放段落
  12. What is the difference between a postulate and a theorem?
      ::假设和定理之间有什么区别?

  播放段落

  For 13-16, use geometric notation to explain each picture in as much detail as possible.
  ::对于13-16,使用几何符号来尽可能详细地解释每一张照片。

  13. 
  14. 
  15. 
  16. 

  播放段落

  For 17-25, determine if the following statements are true or false.
  ::17-25时,确定以下陈述是真实的还是虚假的。

  播放段落
  17. Any two points are collinear.
      ::任何两个点都是共线的。
  播放段落
  18. Any three points determine a plane.
      ::任何三点都决定飞机的位置。
  播放段落
  19. A line is two rays with a common endpoint.
      ::一线是两线,有共同的终点。
  播放段落
  20. A line segment is infinitely many points between two endpoints.
      ::线段是两个终点之间无限多的点。
  播放段落
  21. A point takes up space.
      ::一个点占上空间。
  播放段落
  22. A line is one-dimensional.
      ::一条线是一维的。
  播放段落
  23. Any four points are coplanar.
      ::任何四个点都是共同平面的
  播放段落
  24. $\begin{align*}\overrightarrow{AB}\end{align*}$ could be read “ray $\begin{align*}AB\end{align*}$ ” or “ray $\begin{align*}BA\end{align*}$ .”
      ::AB可以是“射线AB”或“射线BA”。
  播放段落
  25. $\begin{align*}\overleftrightarrow{AB}\end{align*}$ could be read “line $\begin{align*}AB\end{align*}$ ” or “line $\begin{align*}BA\end{align*}$ .”
      ::AB可以是“线性AB”或“线性BA”。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。