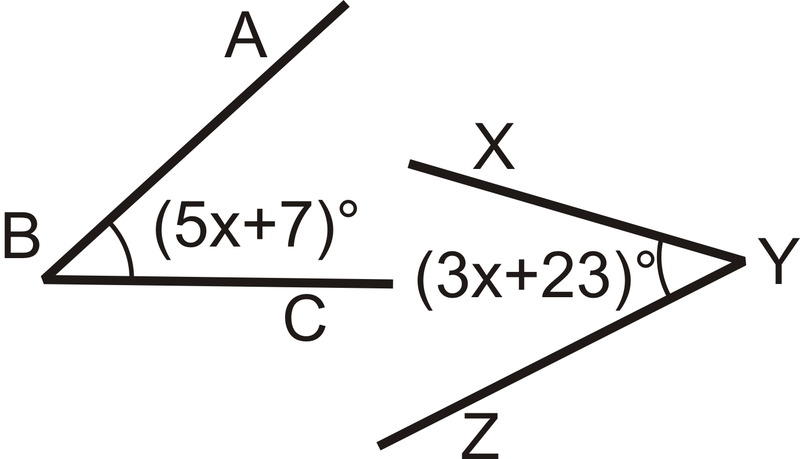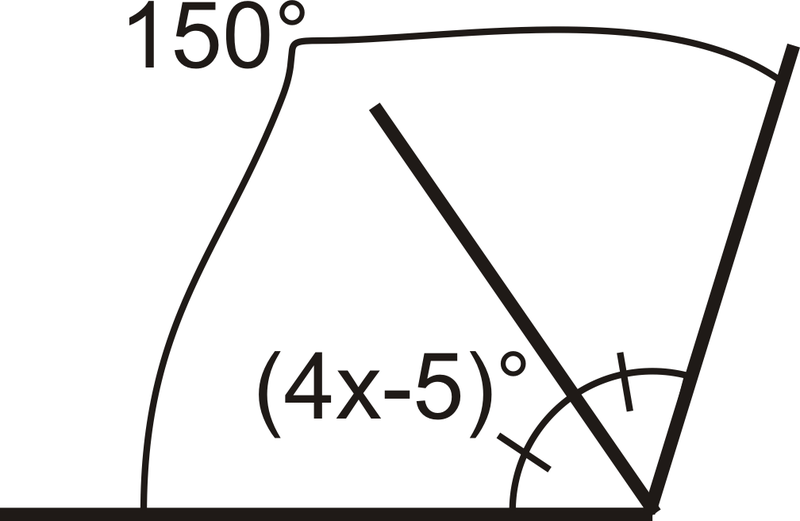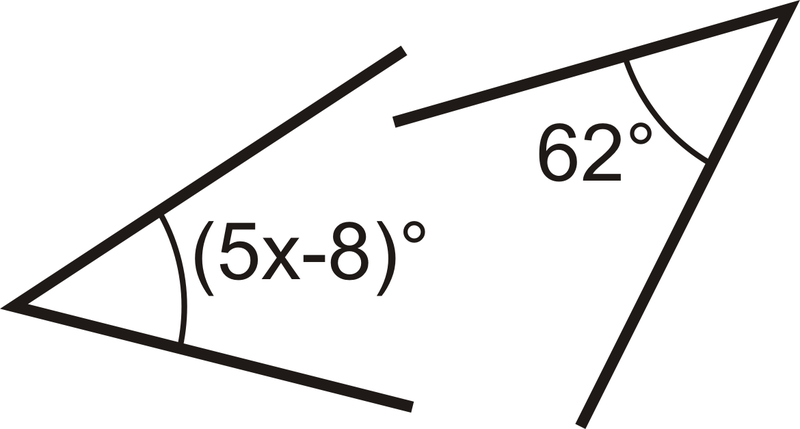1.3 Congruent 角和角双扇形

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section Congruent 切角和角双扇区

  Collapse Expand

  Congruent 切角和角双扇区

  播放段落

  Congruent Angles  and Bisectors
  ::Congruent 圆角和双扇区

  播放段落

  When two geometric figures have the same shape and size (or the same angle measure in the case of angles) they are said to be congruent .
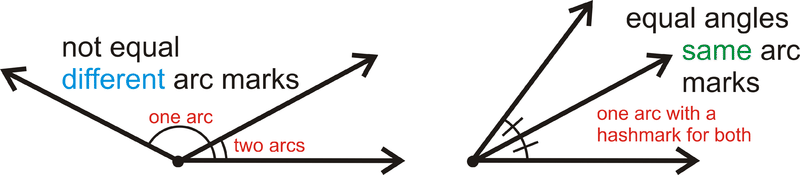
  ::当两个几何数字的形状和大小相同(或角度的角度相同)时,据说它们是一致的。

  Label It	Say It
  $\begin{array}{r}\mathrm{\angle }ABC\cong \mathrm{\angle }DEF\end{array}$	Angle $\begin{array}{r}ABC\end{array}$ is congruent to angle $\begin{array}{r}DEF\end{array}$ .

  播放段落

  If two angles are congruent, then they are also equal. To label equal angles we use angle markings , as shown below:
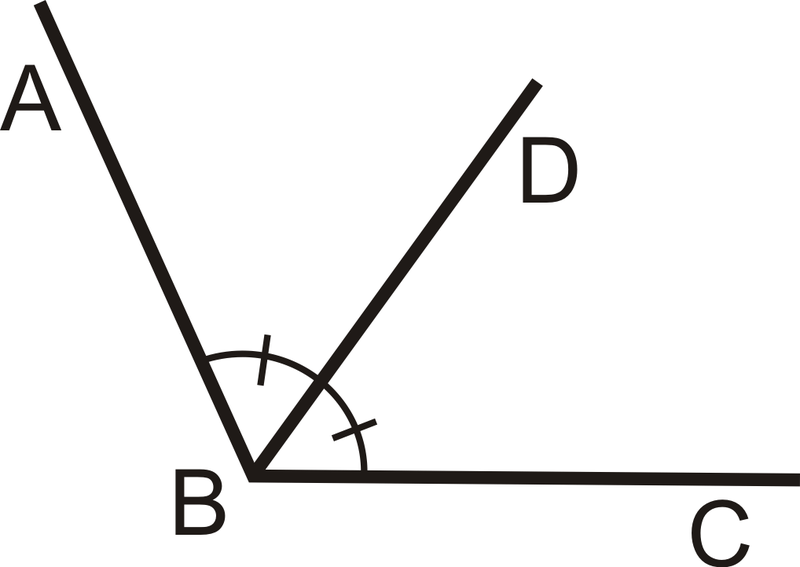
  ::如果两个角度是相同的,那么它们也是相等的。为了给相等角度贴标签,我们使用角标记,如下文所示:

  

  播放段落

  An angle bisector is a line , or a portion of a line, that divides an angle into two congruent angles, each having a measure exactly half of the original angle. Every angle has exactly one angle bisector.
  ::角角对角是一条线,或一条线的一部分,将一个角分为两个相近的角度,每个角度的量度完全等于原来角度的一半。每个角度都完全有一个角角对角。

  

  播放段落

  In the picture above, $\begin{array}{r}\overline{BD}\end{array}$ is the angle bisector of $\begin{array}{r}\mathrm{\angle }ABC\end{array}$ , so $\begin{array}{r}\mathrm{\angle }ABD\cong \mathrm{\angle }DBC\end{array}$ and $\begin{array}{r}m\mathrm{\angle }ABD=\frac{1}{2}m\mathrm{\angle }ABC\end{array}$ .
  ::在以上图中,BD是 ABC的角角, 所以 ABDDDDBC 和 mABD=12mABC 。

  播放段落

  What if you were told that a line segment divides an angle in half? How would you find the measures of the two new angles formed by that segment? 
  ::如果有人告诉你,一个线条段将一个角度分成一半?你将如何发现该段形成的两个新角度的度量?

  播放段落

  Examples
  ::实例

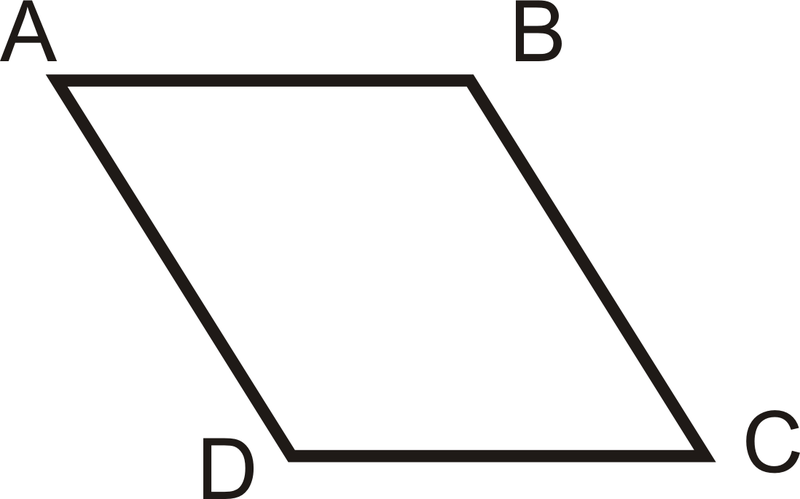
  播放段落

  For Examples  1 and 2, copy the figure below and label it with the following information:
  ::关于例1和例2,抄录下图,并贴上下列资料:

  

  播放段落

  Example 1
  ::例1

  播放段落

  $\begin{array}{r}\mathrm{\angle }A\cong \mathrm{\angle }C\end{array}$
  ::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

  播放段落

  You should have corresponding markings on $\begin{array}{r}\mathrm{\angle }A\end{array}$ and $\begin{array}{r}\mathrm{\angle }C\end{array}$ .
  ::你应该在"Aand"C上有相应的标记

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{array}{r}\mathrm{\angle }B\cong \mathrm{\angle }D\end{array}$
  ::#BD#

  播放段落

  You should have corresponding markings on $\begin{array}{r}\mathrm{\angle }B\end{array}$ and $\begin{array}{r}\mathrm{\angle }D\end{array}$ (that look different from the markings you made in Example 1).
  ::你应该在BandD(与例1中的标记不同)上有相应的标记。

  播放段落

  Example 3
  ::例3

  播放段落

  Write all equal angle statements.
  ::写入所有等角语句 。

  

  播放段落

  $$\begin{array}{rl}m\mathrm{\angle }ADB& =m\mathrm{\angle }BDC=m\mathrm{\angle }FDE={45}^{\circ }\\ m\mathrm{\angle }ADF& =m\mathrm{\angle }ADC={90}^{\circ }\end{array}$$

  
  ::

  播放段落

  Example 4
  ::例4

  播放段落

  What is the measure of each angle?
  ::每个角度的量度是多少?

  

  播放段落

  From the picture, we see that the angles are equal.
  ::从画面来看,我们看到角度是相等的。

  播放段落

  Set the angles equal to each other and solve.
  ::设定对等角度并解析 。

  播放段落

  $$\begin{array}{rl}(5x+7{)}^{\circ }& =(3x+23{)}^{\circ }\\ (2x{)}^{\circ }& ={16}^{\circ }\\ x& =8\end{array}$$

  
  :5x+7) (3x+23) (2x) (16) x=8)

  播放段落

  To find the measure of $\begin{array}{r}\mathrm{\angle }ABC\end{array}$ , plug in $\begin{array}{r}x=8\end{array}$ to
  ::要找到 ABC, 插入 x=8 到

  播放段落

  $\begin{array}{r}(5x+7{)}^{\circ }\to (5(8)+7{)}^{\circ }=(40+7{)}^{\circ }={47}^{\circ }\end{array}$ .
  :5x+7) (5(8))+7) (40+7) (47)。

  播放段落

  Because $\begin{array}{r}m\mathrm{\angle }ABC=m\mathrm{\angle }XYZ,m\mathrm{\angle }XYZ={47}^{\circ }\end{array}$ too.
  ::因为MABC=mXYZ, mXY47也。

  播放段落

  Example 5
  ::例5

  播放段落

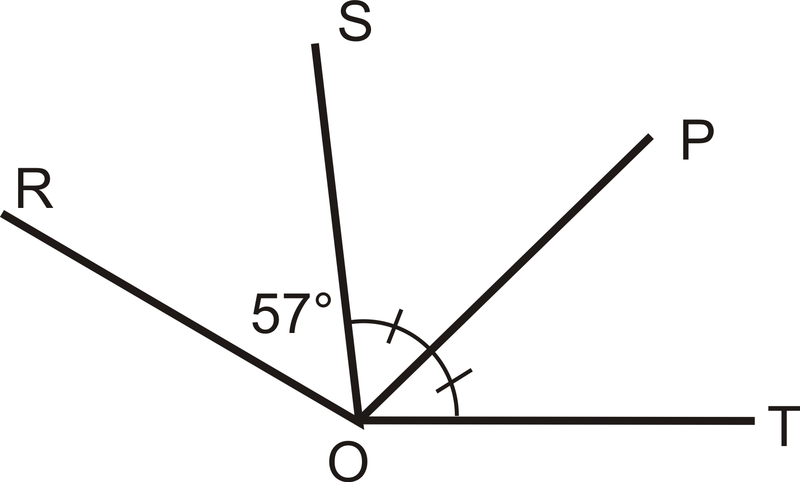
  Is $\begin{array}{r}\overline{OP}\end{array}$ the angle bisector of $\begin{array}{r}\mathrm{\angle }SOT\end{array}$ ?
  ::索特的角是分角吗?

  

  播放段落

  Yes, $\begin{array}{r}\overline{OP}\end{array}$ is the angle bisector of $\begin{array}{r}\mathrm{\angle }SOT\end{array}$ from the markings in the picture.
  ::是的, OKOT的角 从图片的标记的两侧角。

  播放段落

  Review
  ::回顾

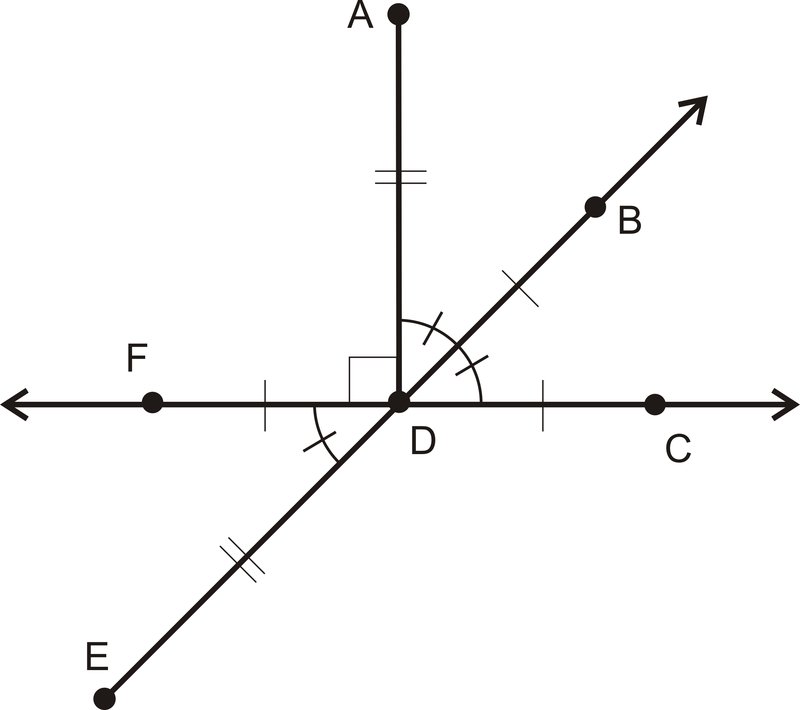
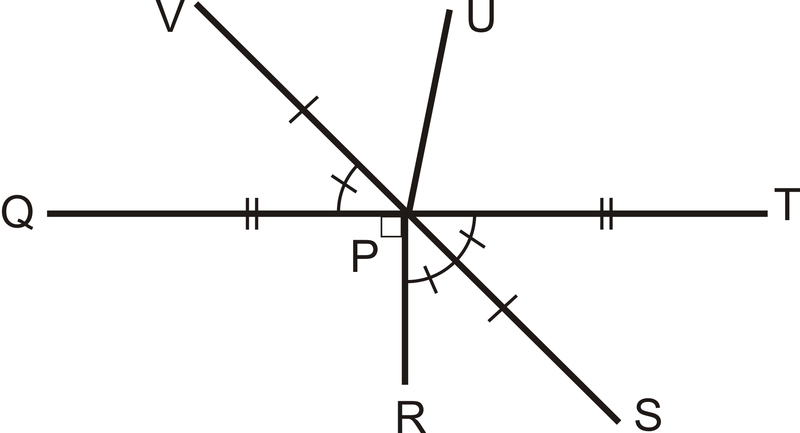
  播放段落

  For 1-4, use the following picture to answer the questions.
  ::1-4,使用以下图片回答问题。

  

  播放段落
  1. What is the angle bisector of $\begin{array}{r}\mathrm{\angle }TPR\end{array}$ ?
     ::“TPR”的视角是什么?
  播放段落
  2. What is $\begin{array}{r}m\mathrm{\angle }QPR\end{array}$ ?
     ::什么是MPR?
  播放段落
  3. What is $\begin{array}{r}m\mathrm{\angle }TPS\end{array}$ ?
     ::什么是MTPS?
  播放段落
  4. What is $\begin{array}{r}m\mathrm{\angle }QPV\end{array}$ ?
     ::什么是PV?

  播放段落

  For 5-6, use algebra to determine the value of variable in each problem.
  ::对于5-6,使用代数来确定每个问题变量的价值。

  5. 
  6. 

  播放段落

  For 7-10, decide if the statement is true or false.
  ::7-10,决定声明是真实还是虚假。

  播放段落
  7. Every angle has exactly one angle bisector.
     ::每个角度都有一个截面角
  播放段落
  8. Any marking on an angle means that the angle is $\begin{array}{r}{90}^{\circ }\end{array}$ .
     ::角上的任何标记表示角为 90 。
  播放段落
  9. An angle bisector divides an angle into three congruent angles.
     ::角对角区将角分为三个相容角度。
  播放段落
  10. Congruent angles have the same measure.
      ::共形角度具有相同的度量。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。