Course: 1.4 中点和分段 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 中点和分段

Collapse Expand
中点和分段
Midpoints and Segment Bisectors
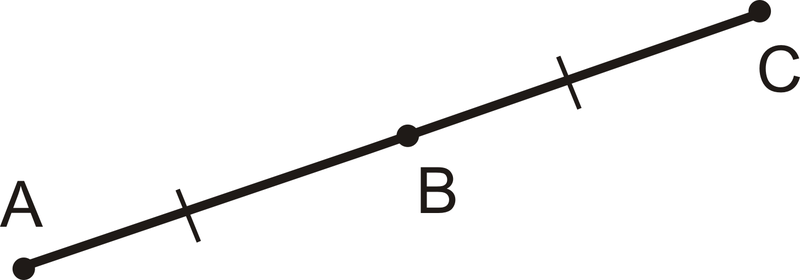
::中点和分段

When two segments are congruent , we indicate that they are congruent, or of equal length, with segment markings , as shown below:
::当两个部分相互一致时,我们表示它们相互一致,或长度相等,并有段段标记,如下所示:

A midpoint is a point on a line segment that divides it into two congruent segments.
::中点是一个线段的点, 将其分为两个相容的段。

Because $\begin{aligned} A B = B C, B \end{aligned}$ is the midpoint of $\begin{aligned} \bar{A C} \end{aligned}$ . Any line segment will have exactly one midpoint.
::因为AB=BC, B是AC的中点。任何线段都会有一个中点。

When points are plotted in the coordinate plane , we can use a formula to find the midpoint between them.
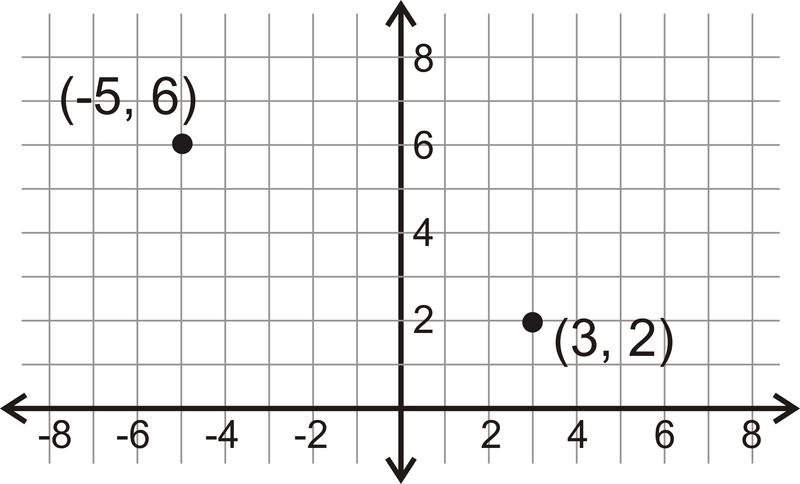
::当点在坐标平面中绘制时,我们可以使用一个公式来找到它们之间的中点。

Here are two points, (-5, 6) and (3, 2).
::以下是两点(5、6和3、2),即两点(5、6)和两点(3、2)。

The midpoint should be halfway between the points on the segment connecting them. Just by looking, it seems like the midpoint is (-1, 4).
::中点应该介于连接点的中间点之间。仅看一看, 中点似乎是( 1 - 4 ) 。

: For two points, $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} x_{2}, y_{2} \end{aligned}$ , the midpoint is $\begin{aligned} (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2}) \end{aligned}$ .
:::两个点(x1,y1)和x2,y2,中点为(x1+x22,y1+y22)。

Let’s use the formula to make sure (-1, 4) is the midpoint between (-5, 6) and (3, 2).
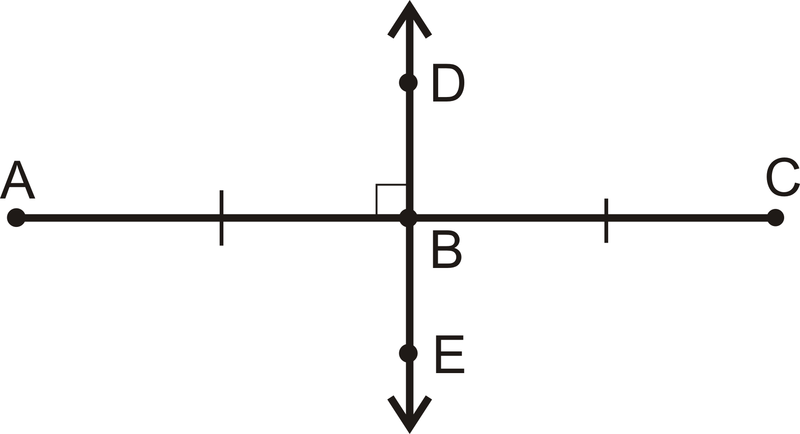
::让我们使用公式确定(-1, 4)是中点(-5, 6)和(3, 2)之间。

$\begin{aligned} (\frac{- 5 + 3}{2}, \frac{6 + 2}{2}) = (\frac{- 2}{2}, \frac{8}{2}) = (- 1, 4) \end{aligned}$

A segment bisector cuts a line segment into two congruent parts and passes through the midpoint. A perpendicular bisector is a segment bisector that intersects the segment at a right angle .
::分形双向分形将线段切成两个相容的部位,然后通过中点。垂直双向分形是一个分形分形,从正确的角度将段段相交。

$\begin{aligned} \bar{A B} ≅ \bar{B C} \\ \bar{A C} ⊥ \overset{\leftrightarrow}{D E} \end{aligned}$

::AB -BC -AC -DE -AB -BC -AC AC -DE

What if you were given the coordinates of two points and you wanted to find the point exactly in the middle of them? How would you find the coordinates of this third point?
::如果你们获得两个点的坐标,而你们想在两点中间找到点呢?你们如何找到第三个点的坐标?

Examples
::实例

Example 1
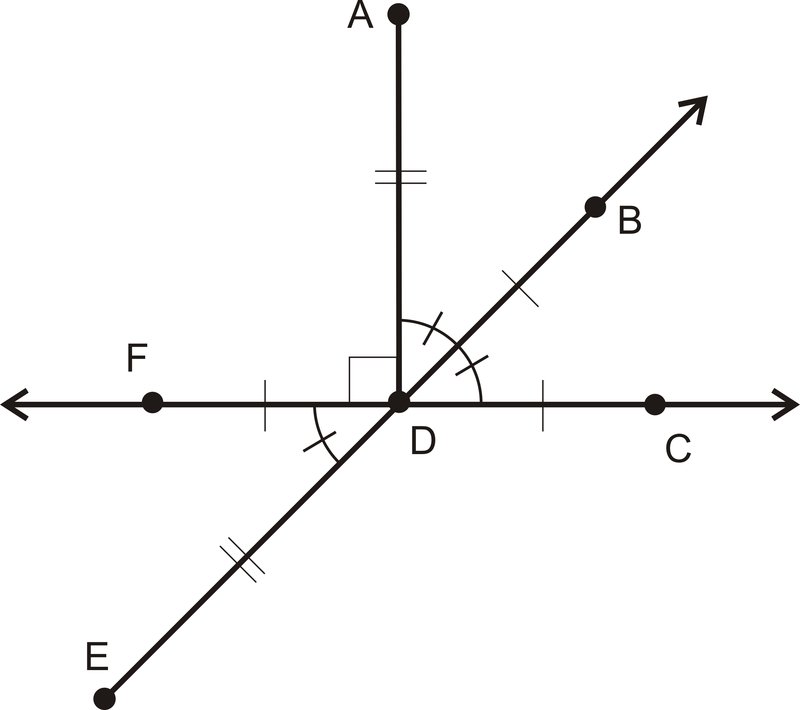
::例1

Write all equal segment statements.
::写入全部相等的区段语句语句。

$\begin{aligned} A D & = D E \\ F D & = D B = D C \end{aligned}$

::AD=DEFD=DB=DC=DD=DC=DD=DD=DD=DD=DD=DD=DC=DD=DDD=DD=DD=DD=DD=DD=DD=DD=DD=DD=DDD=DC

Example 2
::例2

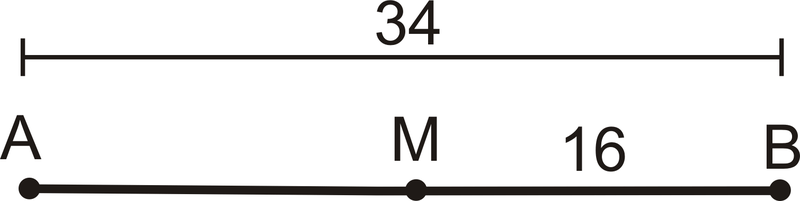
Is $\begin{aligned} M \end{aligned}$ a midpoint of $\begin{aligned} \bar{A B} \end{aligned}$ ?
::M是AB的中点吗?

No, it is not $\begin{aligned} M B = 16 \end{aligned}$ and $\begin{aligned} A M = 34 - 16 = 18 \end{aligned}$ . $\begin{aligned} A M \end{aligned}$ must equal $\begin{aligned} M B \end{aligned}$ in order for $\begin{aligned} M \end{aligned}$ to be the midpoint of $\begin{aligned} \bar{A B} \end{aligned}$ .
::MB=16和AM=34-16=18。AM必须等于MB才能使M成为AB的中点。

Example 3
::例3

Find the midpoint between (9, -2) and (-5, 14).
::查找中点在(9,2)和(5,14)之间。

Plug the points into the formula.
::将点插入公式中。

$\begin{aligned} (\frac{9 + (- 5)}{2}, \frac{- 2 + 14}{2}) = (\frac{4}{2}, \frac{12}{2}) = (2, 6) \end{aligned}$

Example 4
::例4

Which line is the perpendicular bisector of $\begin{aligned} \bar{M N} \end{aligned}$ ?
::哪条线是MN的垂直双侧线?

The perpendicular bisector must bisect $\begin{aligned} \bar{M N} \end{aligned}$ and be perpendicular to it. Only $\begin{aligned} \overset{\leftrightarrow}{O Q} \end{aligned}$ fits this description. $\begin{aligned} \overset{\leftrightarrow}{S R} \end{aligned}$ is a bisector, but is not perpendicular.
::垂直的两分形必须双切, 并且与它垂直。只有这个描述才符合这个描述。 SR 是一个双分形, 但不是垂直的。

Example 5
::例5

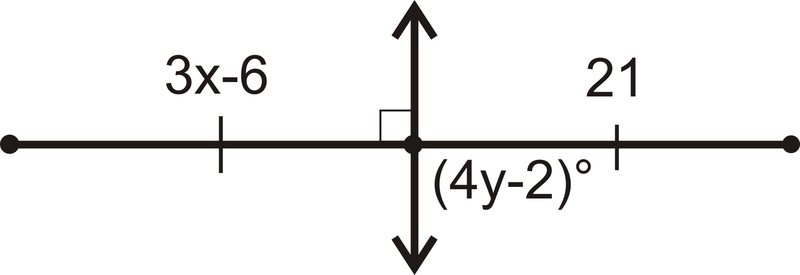
Find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::查找 x 和 y 。

The line shown is the perpendicular bisector.
::所显示的直线是垂直的双向线段。

$\begin{aligned} So, 3 x - 6 & = 21 & And, (4 y - 2)^{\circ} = 90^{\circ} \\ 3 x & = 27 & 4 y = 92^{\circ} \\ x & = 9 & y = 23^{\circ} \end{aligned}$

::所以, 3x-6=21和, (4y-2) 903x=27 4y=92x=9y=23

Review
::回顾

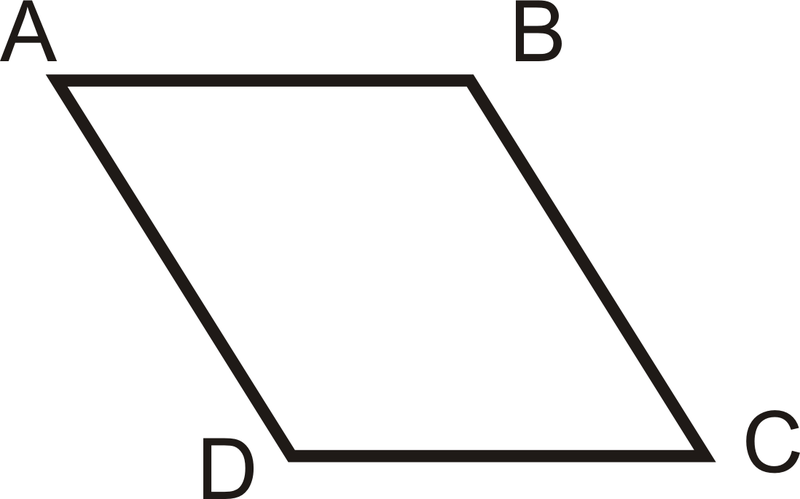
Copy the figure below and label it with the following information:
::复制下图,并贴上以下信息标签:

$\begin{aligned} \bar{A B} & ≅ \bar{C D} \\ \bar{A D} & ≅ \bar{B C} \end{aligned}$

::AB , , , , 已经 , 已经 , 已经 , 已经 , 已经 , 已经 , 已经 , 已经 , 已经 , 已经了

For 2-4, use the following picture to answer the questions.
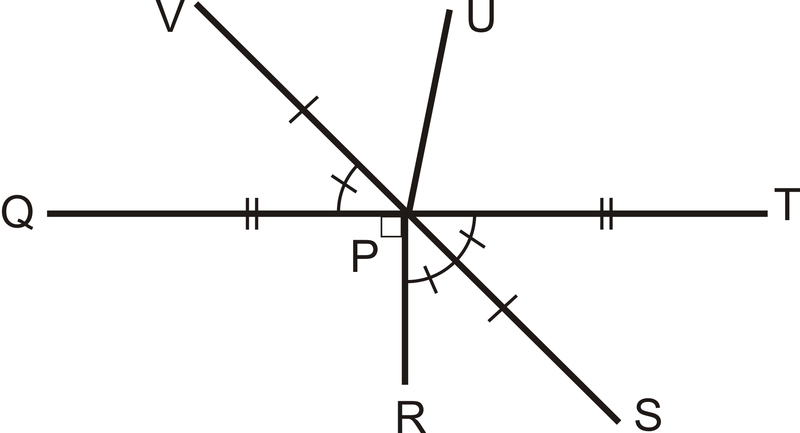
::2-4,使用下图解回答问题。

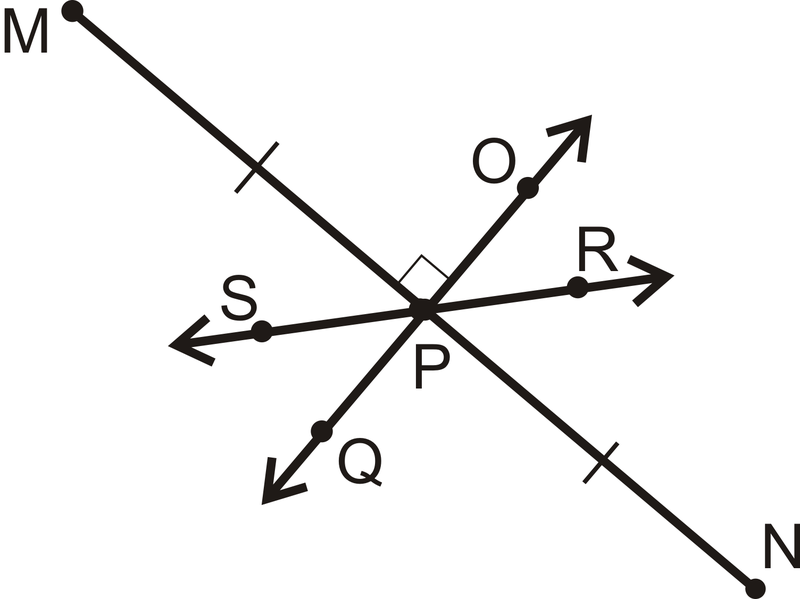
$\begin{aligned} P \end{aligned}$ is the midpoint of what two segments?
::P是两个部分的中点?

How does $\begin{aligned} \bar{V S} \end{aligned}$ relate to $\begin{aligned} \bar{Q T} \end{aligned}$ ?
::VS和QT有什么关系?

How does $\begin{aligned} \bar{Q T} \end{aligned}$ relate to $\begin{aligned} \bar{V S} \end{aligned}$ ?
::QT和VS有什么关系?

For exercise 5, use algebra to determine the value of $\begin{aligned} x . \end{aligned}$
::在练习5中,使用代数确定 x 值。

For questions 6-10, find the midpoint between each pair of points.
::问题6-10,找到每对点之间的中点。

(-2, -3) and (8, -7)
:-2,-3)和(8,-7)

(9, -1) and (-6, -11)
:9,-1)和(6,-11)

(-4, 10) and (14, 0)
:4, 10)和(14, 0)

(0, -5) and (-9, 9)
:0,5和9,9)

(-3, -5) and (2, 1)
:3-3-5)和(2,1)

Given the midpoint $\begin{aligned} (M) \end{aligned}$ and either endpoint of $\begin{aligned} \bar{A B} \end{aligned}$ , find the other endpoint.
::考虑到AB的中点(M)和终点,请找到另一个终点。

$\begin{aligned} A (- 1, 2) \end{aligned}$ and $\begin{aligned} M (3, 6) \end{aligned}$
::A(1,2)和M(3,6)

$\begin{aligned} B (- 10, - 7) \end{aligned}$ and $\begin{aligned} M (- 2, 1) \end{aligned}$
::B-(10,-7)和M(-2,2,1)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

中点和分段

Midpoints and Segment Bisectors ::中点和分段

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Midpoints and Segment Bisectors
::中点和分段

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)