1.11 三角分类

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三角三角分类

  Collapse Expand

  三角三角分类

  播放段落

  Classifying Triangles
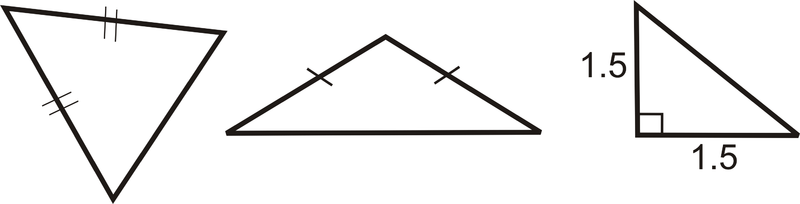
  ::分类三角形

  播放段落

  A triangle is any closed figure made by three line segments intersecting at their endpoints. Every triangle has three vertices (the points where the segments meet), three sides (the segments), and three interior angles (formed at each vertex). All of the following shapes are triangles.
  ::三角形是指由三个线段在端点交叉而成的任何封闭形。每个三角形都有三个顶点(部分相交点)、三个边(部分相交点)、三个内角(每个顶点形成)。以下形状均为三角形。

  

  播放段落

  The sum of the interior angles in a triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ . This is called the Triangle Sum Theorem and is discussed further in the "Triangle Sum Theorem" concept.
  ::三角形内角的总和为 180 。 这称为三角形 Sum 理论, 并在“ 三角 Sum 理论” 概念下进一步讨论 。

  播放段落

  Angles can be classified by their size as acute, obtuse or right. In any triangle, two of the angles will always be acute. The third angle can be acute, obtuse, or right. We classify each triangle by this angle .
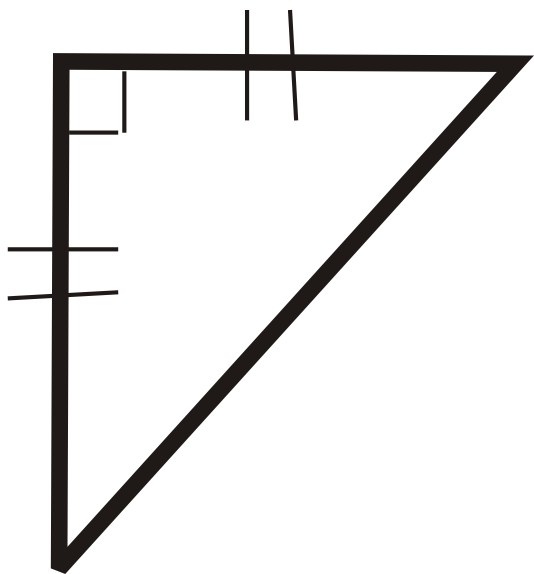
  ::角度可以按其大小分类为急性、 模糊或右。 在任何三角形中, 两个角度总是急性。 第三个角度可以是急性、 模糊或右。 我们按此角度将每个三角形分类 。

  播放段落

  Right Triangle : A triangle with one right angle .
  ::右三角:一个右角三角形。

  

  播放段落

  Obtuse Triangle : A triangle with one obtuse angle .
  ::阻塞三角形:一个三角形,一个斜角。

  

  播放段落

  Acute Triangle : A triangle where all three angles are acute.
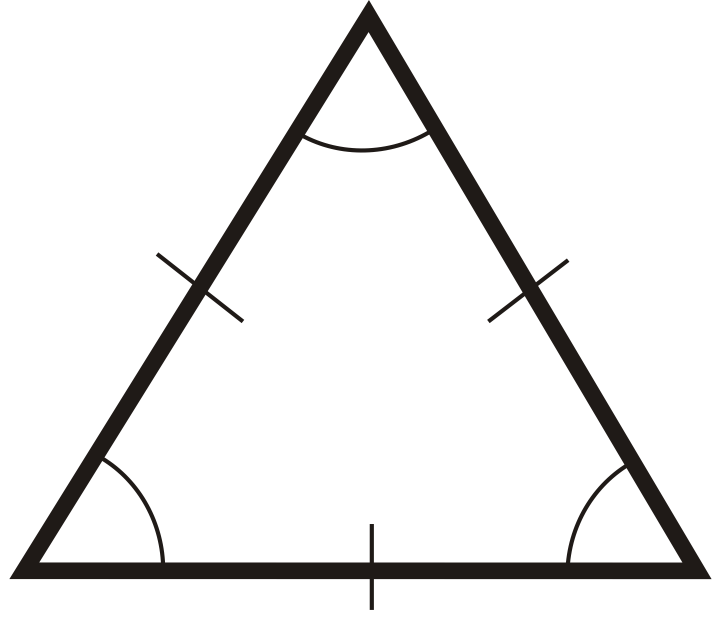
  ::急性三角形:三角形,其中所有三个角度都是急性的。

  

  播放段落

  Equiangular Triangle : A triangle where all the angles are congruent .
  ::等角三角形:一个三角形,所有角度都相似。

  

  播放段落

  You can also classify a triangle by its sides.
  ::您也可以按三角形的侧面进行分类。

  播放段落

  Scalene Triangle : A triangle where all three sides are different lengths.
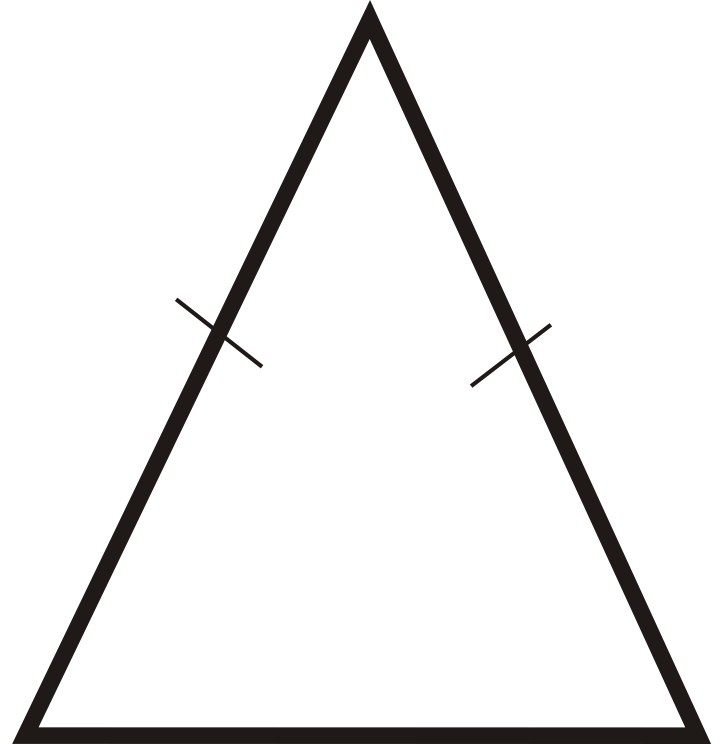
  ::缩放三角形: 一个三角形, 其中所有三边的长度不同 。

  

  播放段落

  Isosceles Triangle : A triangle with at least two congruent sides.
  ::Isosceles三角形:一个至少有两个相容面的三角形。

  

  播放段落

  : A triangle with three congruent sides.
  :::一个三角形,有三个相容的两面。

  

  播放段落

  Note that from the definitions, an equilateral triangle is also an isosceles triangle.
  ::请注意,从定义上看,等边三角形也是等边三角形。

  播放段落

  What if you were given the angle measures and/or side lengths of a triangle? How would you describe the triangle based on that information?
  ::如果给您一个三角形的角度量和(或)侧长, 您将如何描述基于此信息的三角形 ?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Which of the figures below are not triangles?
  ::以下哪些数字不是三角形?

  

  播放段落

  $\begin{array}{r}B\end{array}$ is not a triangle because it has one curved side. $\begin{array}{r}D\end{array}$ is not closed, so it is not a triangle either.
  ::B 不是三角形, 因为它有一个弯曲的侧面。 D 没有关闭, 所以它也不是三角形 。

  播放段落

  Example 2
  ::例2

  播放段落

  How many triangles are in the diagram below?
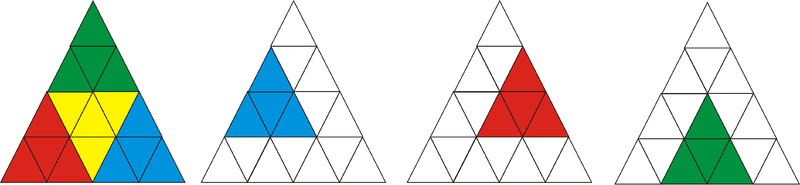
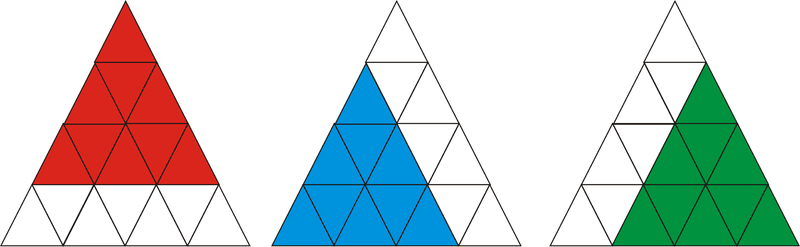
  ::下面的图表中有多少三角形?

  

  播放段落

  Start by counting the smallest triangles, 16.
  ::开始计数最小的三角形 16

  播放段落

  Now count the triangles that are formed by 4 of the smaller triangles, 7.
  ::现在计数由4个小三角形组成的三角形,7个小三角形组成的三角形。

  

  播放段落

  Next, count the triangles that are formed by 9 of the smaller triangles, 3.
  ::接下来,数下由9个小三角形组成的三角形,3个小三角形组成的三角形。

  

  播放段落

  Finally, there is the one triangle formed by all 16 smaller triangles. Adding these numbers together, we get $\begin{array}{r}16+7+3+1=27\end{array}$ .
  ::最后,有一个由所有16个小三角形组成的三角形。加上这些数字,我们得到16+7+3+1=27。

  播放段落

  Example 3
  ::例3

  播放段落

  True or false: An equilateral triangle is equiangular.
  ::真实的或假的: 等边三角形是等角 。

  播放段落

  True. Equilateral triangles have interior angles that are all congruent so they are equiangular.
  ::正确。 等边三角形的内角是相同的,因此是等角。

  播放段落

  Example 4
  ::例4

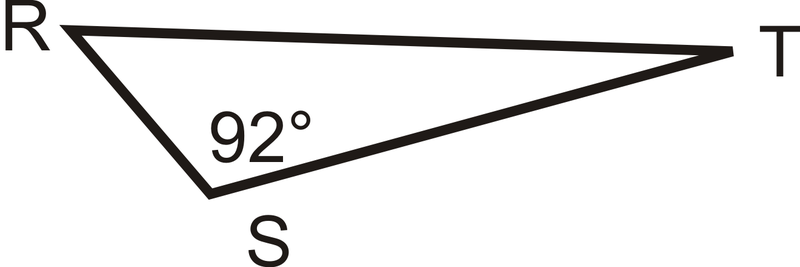
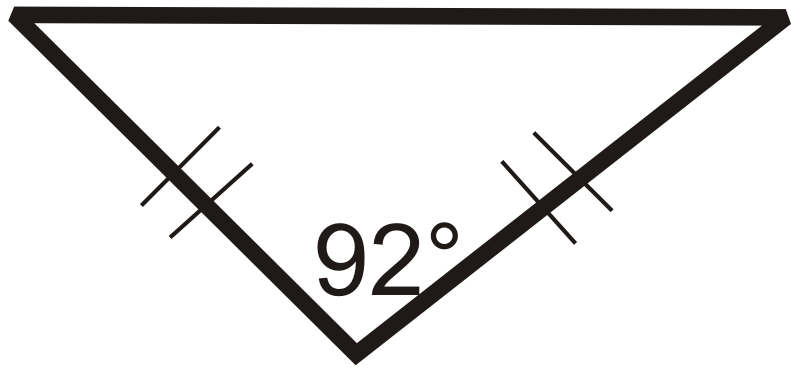
  播放段落

  Which term best describes $\begin{array}{r}\mathrm{△}RST\end{array}$ below?
  ::哪个词最能描述下面的“RST”?

  

  播放段落

  This triangle has one labeled obtuse angle of $\begin{array}{r}{92}^{\circ }\end{array}$ . Triangles can have only one obtuse angle, so it is an obtuse triangle.
  ::此三角形有一个标记的隐性角为 92 。 三角形只能有一个隐性角, 所以它是一个隐性三角形 。

  播放段落

  Example 5
  ::例5

  播放段落

  Classify the triangle by its sides and angles.
  ::按三角形的侧面和角度对三角形进行分类。

  

  播放段落

  We see that there are two congruent sides, so it is isosceles. By the angles, they all look acute. We say this is an acute isosceles triangle.
  ::我们看到两个相容的两面, 所以是等分形。从角度看, 它们看起来都很尖锐。我们说这是一个急性等分形三角形。

  播放段落

  Review
  ::回顾

  播放段落

  For questions 1-6, classify each triangle by its sides and by its angles.
  ::对于问题1-6,按三角形的侧面和角度对三角形进行分类。

  1. 
  2. 
  3. 
  4. 
  5. 
  6. 
  播放段落
  7. Can you draw a triangle with a right angle and an obtuse angle? Why or why not?
     ::您能否用右角度和斜角度绘制三角形? 为什么或为何不绘制三角形 ?
  播放段落
  8. In an isosceles triangle, can the angles opposite the congruent sides be obtuse?
     ::在等分形三角形中,对齐方对面的角能否模糊不清?

  播放段落

  For 9-10, determine if the statement is true or false.
  ::9-10,确定声明是真实还是虚假。

  播放段落
  9. Obtuse triangles can be isosceles.
     ::阻力三角形可以是等离子体。
  播放段落
  10. A right triangle is acute.
      ::右三角是急性的。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源