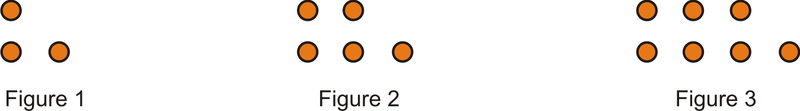2.1 来自模式的引因

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 来自模式的引因

  Collapse Expand

  来自模式的引因

  播放段落

  Inductive Reasoning
  ::引引引理由

  播放段落

  One type of reasoning is inductive reasoning . Inductive reasoning entails making conclusions based upon examples and patterns. Visual patterns and provide good examples of inductive reasoning. Let’s look at some patterns to get a feel for what inductive reasoning is.
  ::一种推理是感性推理。 感性推理需要根据实例和模式做出结论。 视觉模式并提供感性推理的好例子。 让我们看看某些模式,以了解感性推理是什么。

  播放段落

  What if you were given a pattern of three numbers or shapes and asked to determine the sixth number or shape that fit that pattern?
  ::如果给您三个数字或形状的图案 要求您确定符合这个图案的第六个数字或形状呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  A dot pattern is shown below. How many dots would there be in the $\begin{align*}4^{th}\end{align*}$ figure? How many dots would be in the $\begin{align*}6^{th}\end{align*}$ figure?
  ::下面显示点图案。第4位图案将有多少点?第6位图案将有多少点?

  

  播放段落

  Draw a picture. Counting the dots, there are $\begin{align*}4 + 3 + 2 + 1 = 10 \ dots\end{align*}$ .
  ::绘制图片。 计算点数时, 有 4+3+2+1=10 点 。

  

  播放段落

  For the $\begin{align*}6^{th}\end{align*}$ figure, we can use the same pattern, $\begin{align*}6 + 5 + 4 + 3 + 2 + 1\end{align*}$ . There are 21 dots in the $\begin{align*}6^{th}\end{align*}$ figure.
  ::6+5+4+3+2+1。 第6图中有21点。

  播放段落

  Example 2
  ::例2

  播放段落

  How many triangles would be in the $\begin{align*}10^{th}\end{align*}$ figure?
  ::第10位数有多少三角形?

  

  播放段落

  There would be 10 squares in the $\begin{align*}10^{th}\end{align*}$ figure, with a triangle above and below each one. There is also a triangle on each end of the figure. That makes $\begin{align*}10 +10 + 2 = 22\end{align*}$ triangles in all.
  ::第10位图中将有10个方形,每个方形上下有一个三角形。图的每个端端上还有一个三角形。 总共10+10+2=22三角形。

  播放段落

  Example 3
  ::例3

  播放段落

  Look at the pattern 2, 4, 6, 8, 10, $\begin{align*}\ldots\end{align*}$ What is the $\begin{align*}19^{th}\end{align*}$ term in the pattern?
  ::看看模式2,4,6,8,10,... 这个模式的第19个术语是什么?

  播放段落

  Each term is 2 more than the previous term.
  ::每个任期比前一任期多两个任期。

  

  播放段落

  You could count out the pattern until the $\begin{align*}19^{th}\end{align*}$ term, but that could take a while. Notice that the $\begin{align*}1^{st}\end{align*}$ term is $\begin{align*}2 \cdot 1\end{align*}$ , the $\begin{align*}2^{nd}\end{align*}$ term is $\begin{align*}2 \cdot 2\end{align*}$ , the $\begin{align*}3^{rd}\end{align*}$ term is $\begin{align*}2 \cdot 3\end{align*}$ , and so on. So, the $\begin{align*}19^{th}\end{align*}$ term would be $\begin{align*}2 \cdot 19\end{align*}$ or 38.
  ::你可以算出第19个学期之前的模式,但这可能需要一段时间。请注意,第一个学期是21,第二个学期是22,第三个学期是23,等等。因此,第19个学期将是219或38。

  播放段落

  Example 4
  ::例4

  播放段落

  Look at the pattern: 3, 6, 12, 24, 48, $\begin{align*}\ldots\end{align*}$
  ::看这个模式: 3,6,12,24,48,...

  播放段落

  What is the next term in the pattern? What is the $\begin{align*}10^{th}\end{align*}$  term?
  ::下个学期是什么?第十个学期是什么?

  播放段落

  Each term is multiplied by 2 to get the next term.
  ::每个任期乘以 2 以获得下一任期。

            

  播放段落

  Therefore, the next term will be $\begin{align*}48 \cdot 2\end{align*}$ or 96.
  ::因此,下一任期将是482或96。

  播放段落

  To find the $\begin{align*}10^{th}\end{align*}$ term, continue to multiply by 2, or $\begin{align*}3 \cdot \underbrace{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}_{2^9} = 1536\end{align*}$ .
  ::要找到第10个学期,继续乘以2,或3,2,2,2,2,2,2,2,2,2,2,2,29=1536。

  播放段落

  Example 5
  ::例5

  播放段落

  Find the $\begin{align*}8^{th}\end{align*}$ term in the list of numbers: $\begin{align*}2,\frac{3}{4},\frac{4}{9},\frac{5}{16},\frac{6}{25}\ldots\end{align*}$
  ::查找数字列表中的第八学期: 2,34,49,516,625...

  播放段落

  First, change 2 into a fraction, or $\begin{align*}\frac{2}{1}\end{align*}$ . So, the pattern is now $\begin{align*}\frac{2}{1},\frac{3}{4},\frac{4}{9},\frac{5}{16},\frac{6}{25}\ldots\end{align*}$ The top is 2, 3, 4, 5, 6. It increases by 1 each time, so the $\begin{align*}8^{th}\end{align*}$ term’s numerator is 9. The denominators are the square numbers, so the $\begin{align*}8^{th}\end{align*}$ term’s denominator is $\begin{align*}8^2\end{align*}$ or 64. The $\begin{align*}8^{th}\end{align*}$ term is $\begin{align*}\frac{9}{64}\end{align*}$ .
  ::首先,将2变成一个分数,也就是21, 所以,现在的模式是21,34,49,516,625... 上部是2,3,4,5,6,6 上部是2,4,5,6,每次增加1, 所以第八学期的分子数是9, 分母是平方数, 所以第八学期的分母是82或64, 第八学期是964。

  播放段落

  Review
  ::回顾

  播放段落

  For questions 1-3, determine how many dots there would be in the $\begin{align*}4^{th}\end{align*}$ and the $\begin{align*}10^{th}\end{align*}$ pattern of each figure below.
  ::对于问题1-3,确定下图第4位和第10位图案将有多少点。

  1. 
  2. 
  3. 
  播放段落
  4. Use the pattern below to answer the questions.
     播放段落
     1. Draw the next figure in the pattern.
        ::在图案中绘制下一个图案。
     播放段落
     2. How does the number of points in each star relate to the figure number?
        ::每个恒星的点数与数字数字有何关联?
     
     ::使用下面的图案回答问题。在图案中绘制下一个图。每个恒星的点数与图案数有何关联?
  播放段落
  5. Use the pattern below to answer the questions. All the triangles are equilateral triangles.
     播放段落
     1. Draw the next figure in the pattern. How many triangles does it have?
        ::在图案中绘制下一个图。 它有多少三角形 ?
     播放段落
     2. Determine how many triangles are in the $\begin{align*}24^{th}\end{align*}$ figure.
        ::确定第24个图中有多少三角形。
     
     ::使用下面的图案回答问题。所有三角都是等边三角形。在图案中绘制下一个图。它有多少三角形?确定第24图中有多少三角形。

  播放段落

  For questions 6-13, determine: the next three terms in the pattern.
  ::关于问题6-13,确定:模式中的今后三个术语。

  6. 5, 8, 11, 14, 17, $\begin{align*}\ldots\end{align*}$
  7. 6, 1, -4, -9, -14, $\begin{align*}\ldots\end{align*}$
  8. 2, 4, 8, 16, 32, $\begin{align*}\ldots\end{align*}$
  9. 67, 56, 45, 34, 23, $\begin{align*}\ldots\end{align*}$
  10. 9, -4, 6, -8, 3, $\begin{align*}\ldots\end{align*}$
  11. $\begin{align*}\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6} \ldots\end{align*}$
  12. $\begin{align*}\frac{2}{3},\frac{4}{7},\frac{6}{11},\frac{8}{15},\frac{10}{19}, \ldots\end{align*}$
  13. -1, 5, -9, 13, -17, $\begin{align*}\ldots\end{align*}$

  播放段落

  For questions 14-17, determine the next two terms and describe the pattern.
  ::关于问题14-17,确定下两个术语并说明模式。

  14. 3, 6, 11, 18, 27, $\begin{align*}\ldots\end{align*}$
  15. 3, 8, 15, 24, 35, $\begin{align*}\ldots\end{align*}$
  16. 1, 8, 27, 64, 125, $\begin{align*}\ldots\end{align*}$
  17. 1, 1, 2, 3, 5, $\begin{align*}\ldots\end{align*}$

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源