Course: 3.2 垂直直线 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

直直直线

Perpendicular Lines
::直直直线

Two lines are perpendicular when they intersect to form a $\begin{aligned} 90^{\circ} \end{aligned}$ angle . Below, $\begin{aligned} l ⊥ \bar{A B} \end{aligned}$ .
::两条直线相互交叉形成90角角时是垂直的。下面是 l AB 。

In the definition of perpendicular the word “line” is used. However, line segments, rays and planes can also be perpendicular. The image below shows two parallel planes, with a third blue plane that is perpendicular to both of them.
::在垂直定义中,使用了“直线”一词,但线段、射线和平面也可能是直线。下图显示两架平行的平面,第三架蓝平面与这两架飞机都垂直。

Basic Facts about Perpendicular Lines
::关于直直直线的概况

Theorem #1 : If $\begin{aligned} l | | m \end{aligned}$ and $\begin{aligned} n ⊥ l \end{aligned}$ , then $\begin{aligned} n ⊥ m \end{aligned}$ .
::论理1:如果我和Nl,那么nm。

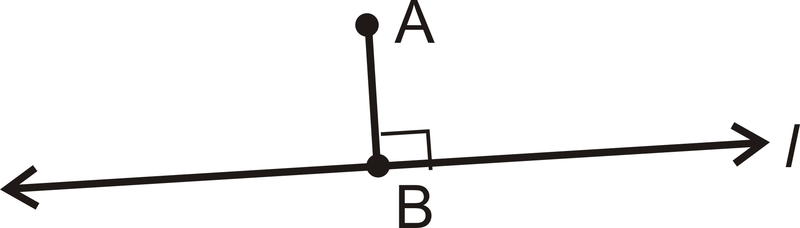
Theorem #2 : If $\begin{aligned} l ⊥ n \end{aligned}$ and $\begin{aligned} n ⊥ m \end{aligned}$ , then $\begin{aligned} l | | m \end{aligned}$ .
::理论2:如果我和NN,那么我就是。

Postulate : For any line and a point not on the line, there is one line perpendicular to this line passing through the point. There are infinitely many lines that pass through $\begin{aligned} A \end{aligned}$ , but only one that is perpendicular to $\begin{aligned} l \end{aligned}$ .
::假设 : 对于任何直线和不在直线上的点, 有一条直线与通过点的直线垂直。有无限多的直线通过 A, 只有一条直线与 I 垂直。

What if you were given a pair of lines that intersect each other at a $\begin{aligned} 90^{\circ} \end{aligned}$ angle? What terminology would you use to describe such lines?
::如果给了你们一对在90°Q角度相互交错的线条呢?用什么术语来形容这些线条?

Examples
::实例

Example 1
::例1

Determine the measure of $\begin{aligned} ∠ 1 \end{aligned}$ .
::确定 #% 1 的量度。

We know that both parallel lines are perpendicular to the transversal .
::我们知道,两条平行线都与横向线紧密相连。

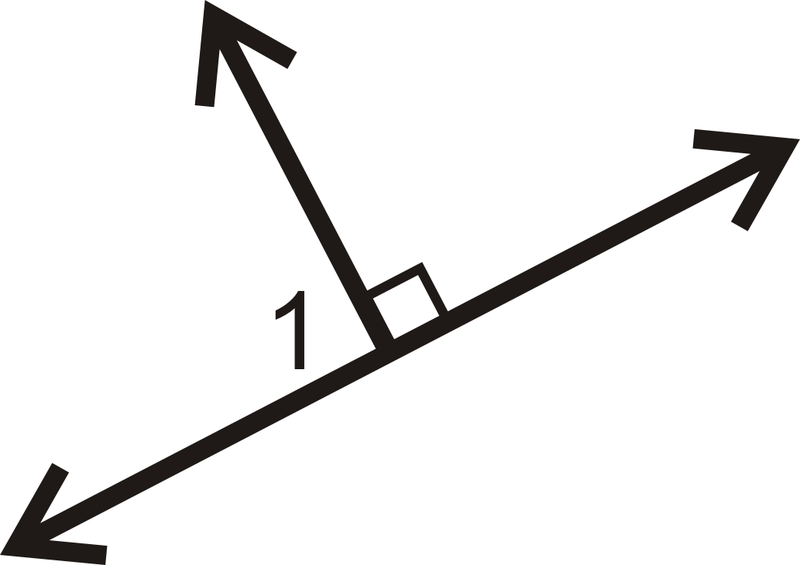
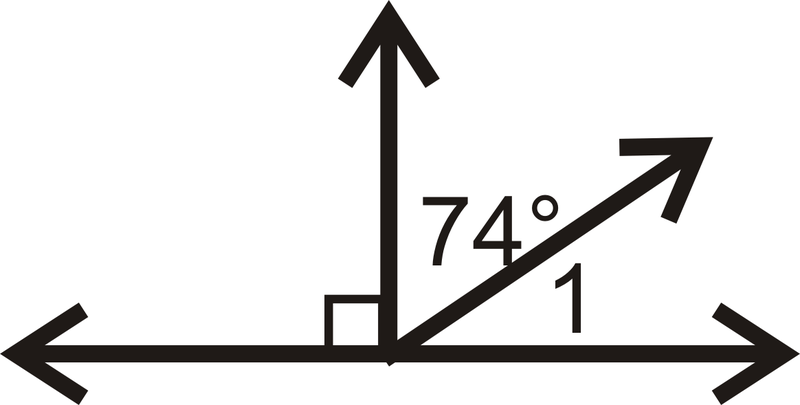
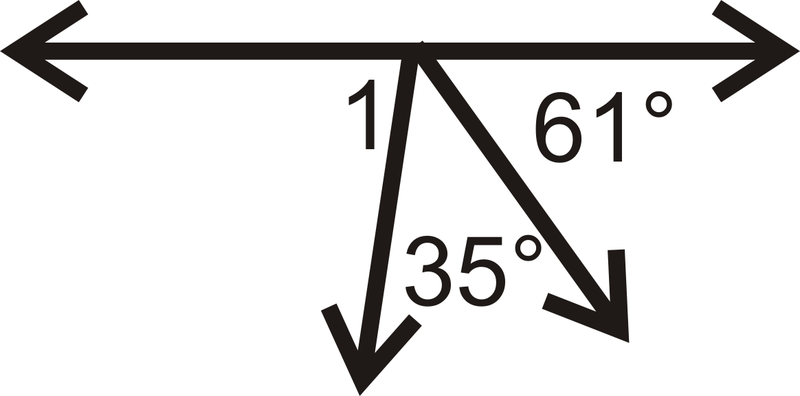
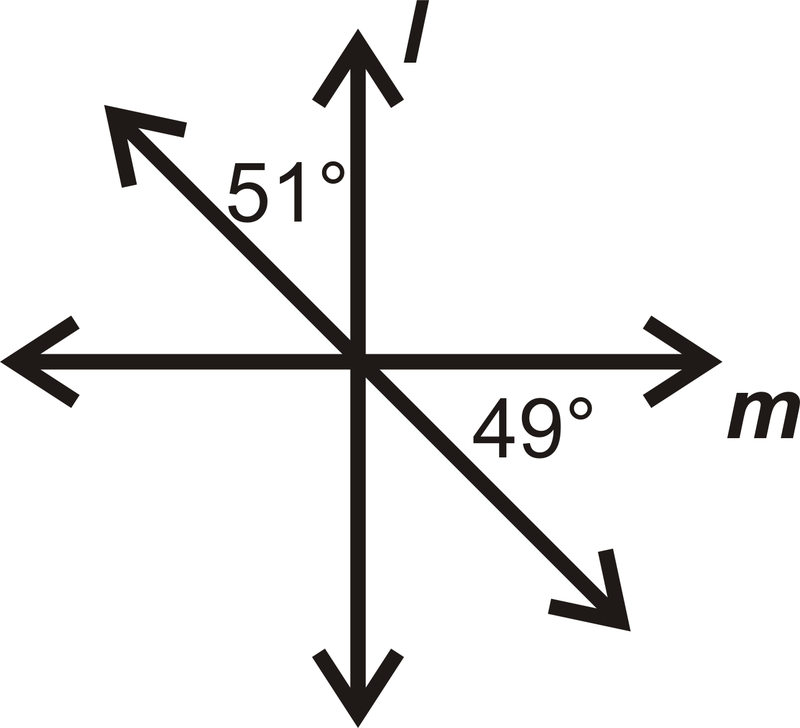
\begin{aligned} m ∠ 1 = 90^{\circ} . \end{aligned}

::m1=90。

Example 2
::例2

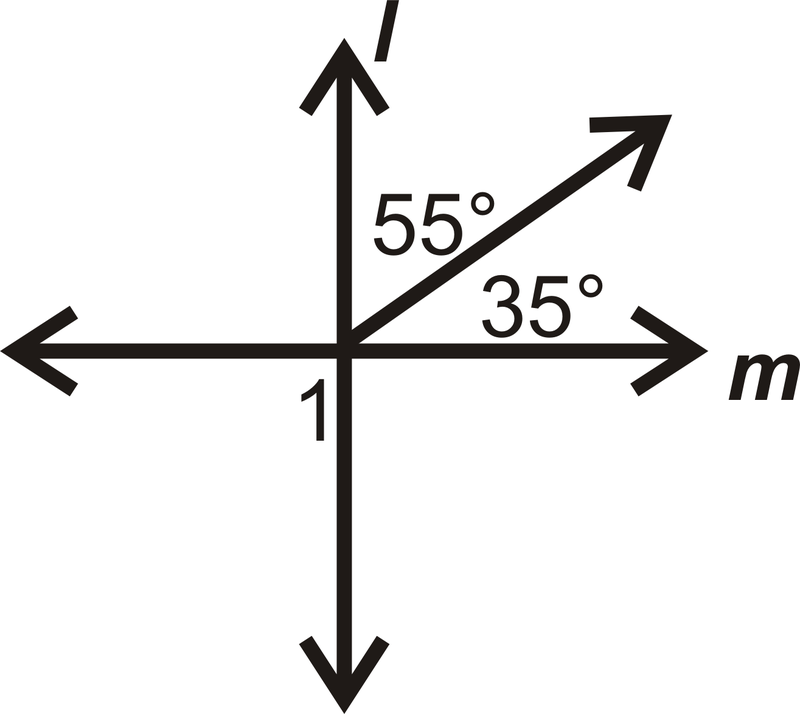
Find $\begin{aligned} m ∠ 1 \end{aligned}$ .
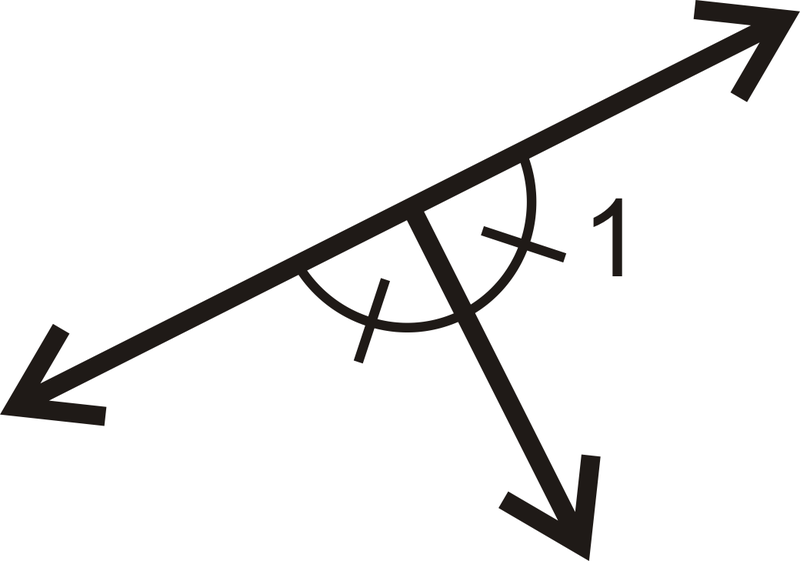
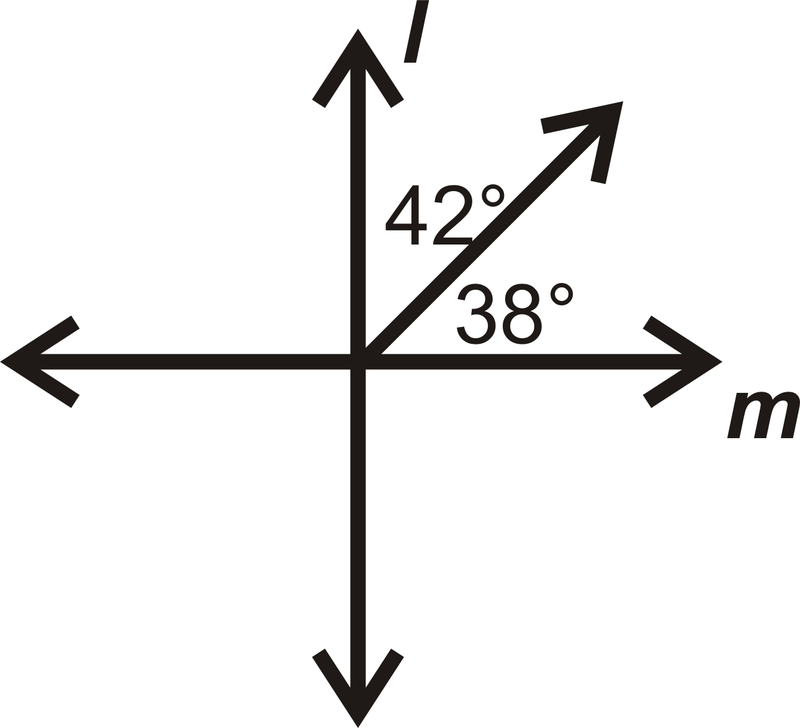
::找到 m1 。

The two adjacent angles add up to $\begin{aligned} 90^{\circ} \end{aligned}$ , so $\begin{aligned} l ⊥ m \end{aligned}$ .
::两个相邻角度加起来等于90,所以...

\begin{aligned} m ∠ 1 = 90^{\circ} \end{aligned}

because it is a vertical angle to the pair of adjacent angles and are congruent .
::m1=90 因为它是一个垂直角度, 与相邻角度对齐, 且相似。

Example 3
::例3

Which of the following is the best example of perpendicular lines : Latitude on a Globe, Opposite Sides of a Picture Frame, Fence Posts, or Adjacent Sides of a Picture Frame?
::以下哪一种是垂直直线的最佳例子:环球纬度、图片框架的对面侧面、栅栏柱或图片框架的对面侧面?

The best example would be adjacent sides of a picture frame. Remember that adjacent means next to and sharing a vertex . The adjacent sides of a picture frame meet at a $\begin{aligned} 90^{\circ} \end{aligned}$ angle and so these sides are perpendicular.
::最好的例子是图片框的相邻侧面。记住相邻指相邻的顶点, 并共享一个顶点。相邻的相邻侧面以 90 角度相交, 因此这些侧面是垂直的。

Example 4
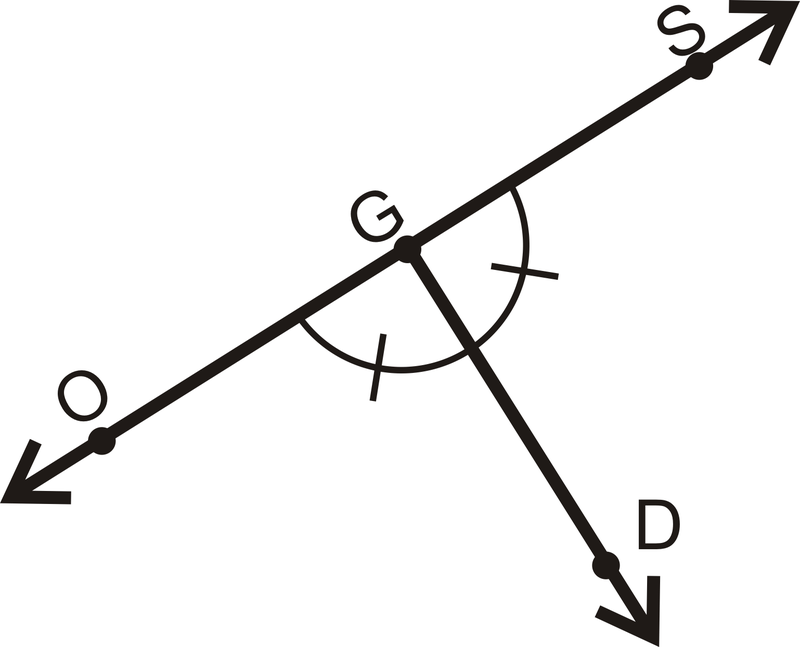
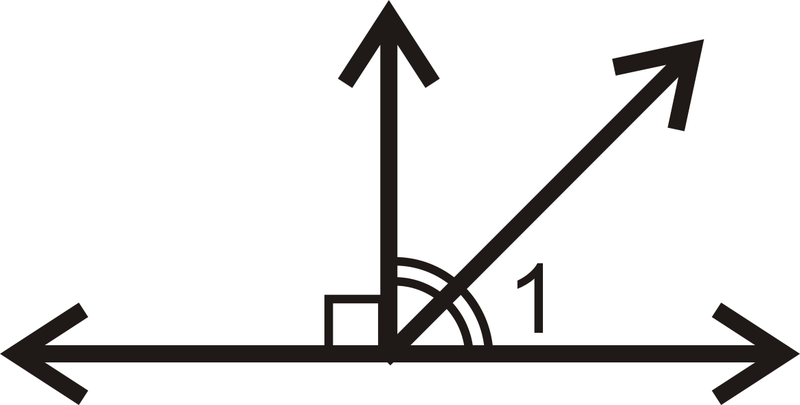
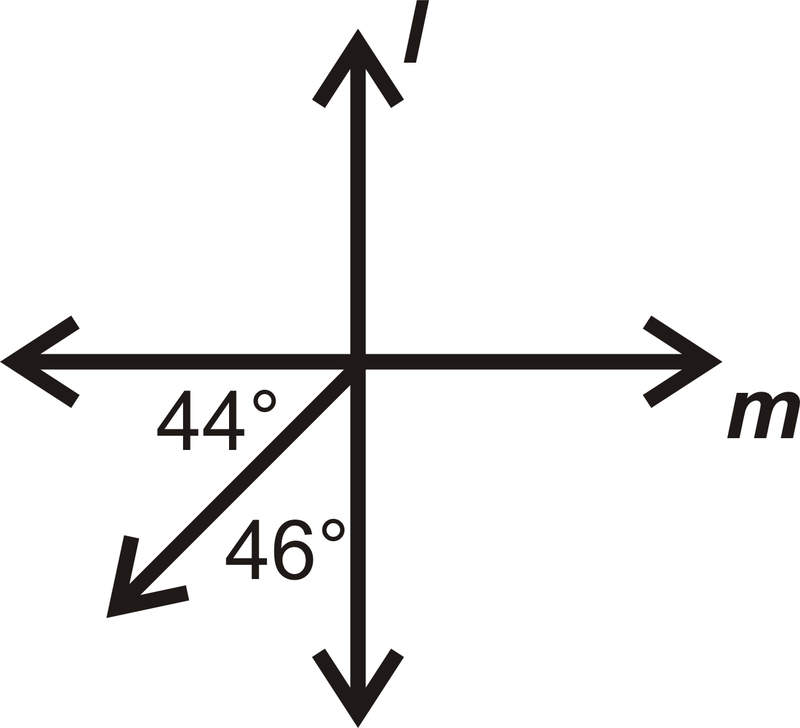
::例4

Is $\begin{aligned} \overset{\leftrightarrow}{S O} ⊥ \vec{G D} \end{aligned}$ ?
::是SOGD?

$\begin{aligned} ∠ O G D ≅ ∠ S G D \end{aligned}$ and the angles form a linear pair . This means both angles are $\begin{aligned} 90^{\circ} \end{aligned}$ , so the lines are perpendicular.
::QOGDSGD 和角度形成线性对。这意味着两个角度都是 90 , 所以线条是垂直的。

Example 5
::例5

Write a 2-column proof to prove Theorem #1. Note: You need to understand in order to understand this proof. If you have not yet learned corresponding angles, be sure to check out that concept first, or skip this example for now.
::写入 2 栏证明来证明理论 # 1 。注意 : 您需要理解才能理解此证据。如果您尚未学习相应的角度, 请务必先检查这个概念, 或者现在跳过这个示例。

Given : $\begin{aligned} l | | m, l ⊥ n \end{aligned}$
::给出: lm, ln

Prove : $\begin{aligned} n ⊥ m \end{aligned}$
::证明:无

*Statement*	*Reason*
1. $\begin{aligned} l \| \| m, l ⊥ n \end{aligned}$	1. Given
2. $\begin{aligned} ∠ 1, ∠ 2, ∠ 3 \end{aligned}$ , and $\begin{aligned} ∠ 4 \end{aligned}$ are right angles	2. Definition of perpendicular lines
3. $\begin{aligned} m ∠ 1 = 90^{\circ} \end{aligned}$	3. Definition of a right angle
4. $\begin{aligned} m ∠ 1 = m ∠ 5 \end{aligned}$	4. Corresponding Angles Postulate
5. $\begin{aligned} m ∠ 5 = 90^{\circ} \end{aligned}$	5. Transitive $\begin{aligned} P o E \end{aligned}$
6. $\begin{aligned} m ∠ 6 = m ∠ 7 = 90^{\circ} \end{aligned}$	6. Congruent Linear Pairs
7. $\begin{aligned} m ∠ 8 = 90^{\circ} \end{aligned}$	7. Vertical Angles Theorem
8. $\begin{aligned} ∠ 5, ∠ 6, ∠ 7 \end{aligned}$ , and $\begin{aligned} ∠ 8 \end{aligned}$ are right angles	8. Definition of right angle
9. $\begin{aligned} n ⊥ m \end{aligned}$	9. Definition of perpendicular lines

Review
::回顾

Use the figure below to answer questions 1-2. The two pentagons are parallel and all of the rectangular sides are perpendicular to both of them.
::使用下图回答问题1-2:两个五边形是平行的,所有长方形的两边都与这两个边都相容。

List a pair of perpendicular lines.
::列出一对垂直直线。

For $\begin{aligned} \bar{A B} \end{aligned}$ , how many perpendicular lines would pass through point $\begin{aligned} V \end{aligned}$ ? Name this/these line(s).
::对于AB ' 来说,有多少垂直直径线通过点五? 请列出这条/这几条线。

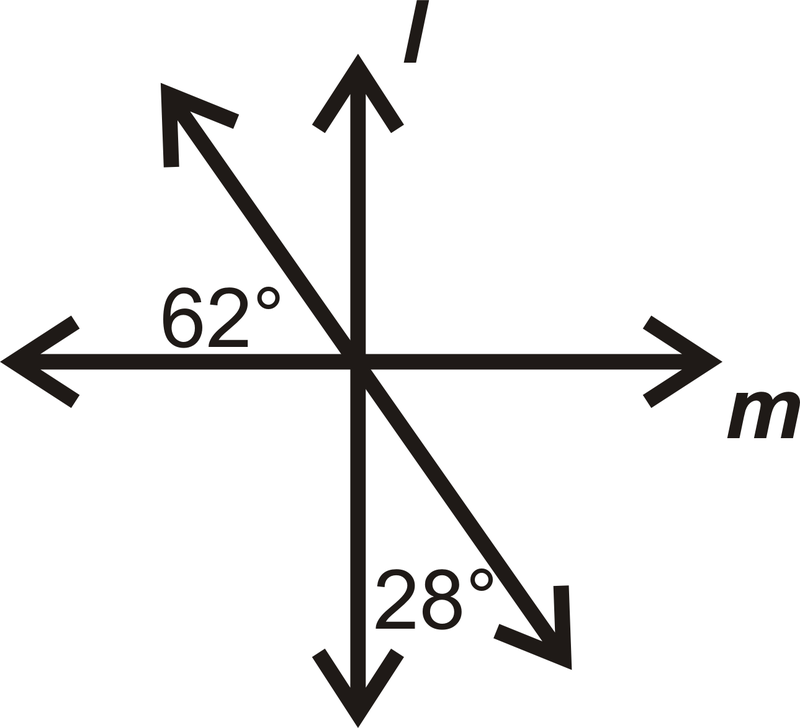
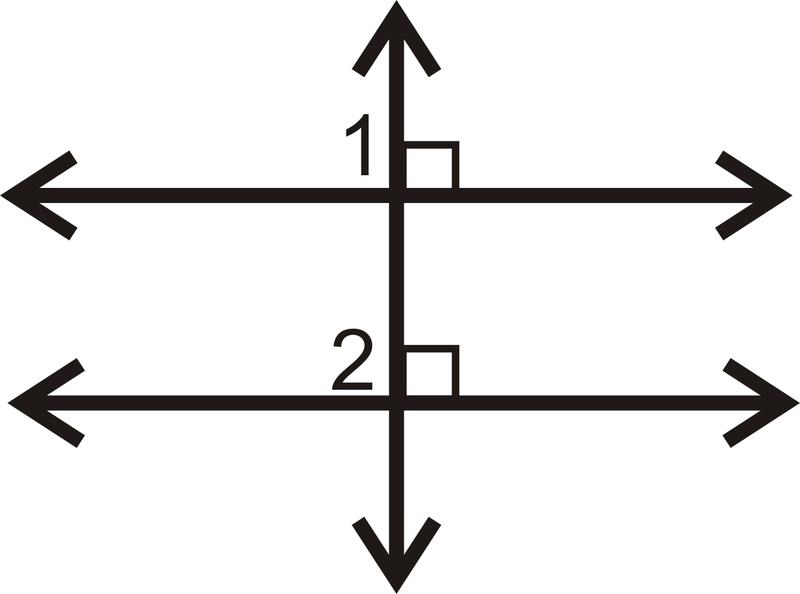
Use the picture below for question 3.
::问题3使用下面的图景。

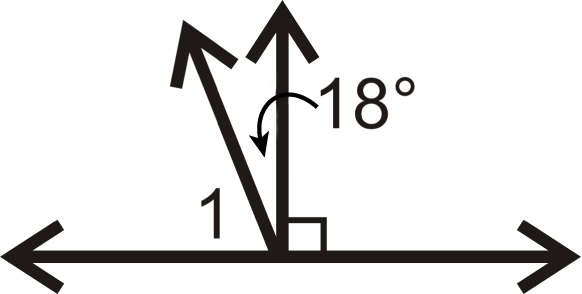
If $\begin{aligned} t ⊥ l \end{aligned}$ , is $\begin{aligned} t ⊥ m \end{aligned}$ ? Why or why not?
::如果tl,是tm?为什么或为什么不呢?

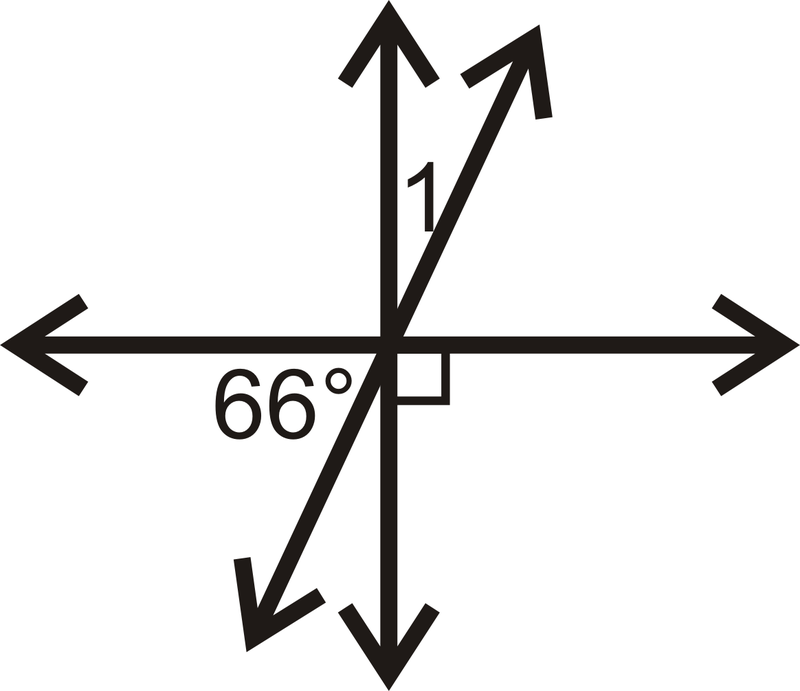
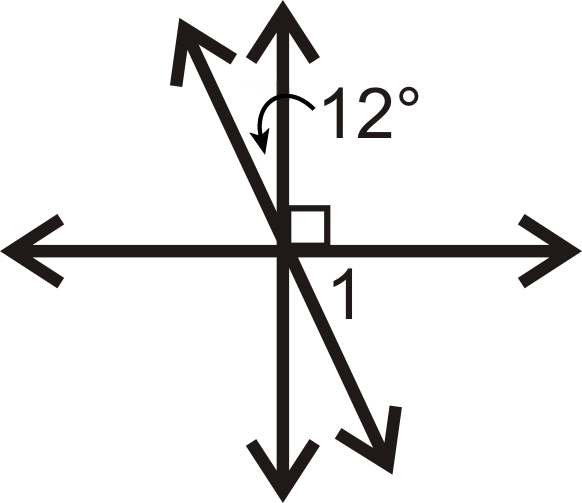
Find the measure of $\begin{aligned} ∠ 1 \end{aligned}$ for each problem below.
::找到以下每个问题的 #% 1 的度量。

In questions 13-16, determine if $\begin{aligned} l ⊥ m \end{aligned}$ .
::在问题13-16中,确定是否

Fill in the blanks in the proof below.
::填充以下证据中的空白。

Given : $\begin{aligned} l ⊥ m, l ⊥ n \end{aligned}$ Prove : $\begin{aligned} m | | n \end{aligned}$
::给出: lm, ln prove: mn

*Statement*	*Reason*
1.	1.
2. $\begin{aligned} ∠ 1 \end{aligned}$ and $\begin{aligned} ∠ 2 \end{aligned}$ are right angles	2.
3.	3. Definition of right angles
4.	4. Transitive $\begin{aligned} P o E \end{aligned}$
5. $\begin{aligned} m \| \| n \end{aligned}$	5.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

直直直线

Perpendicular Lines ::直直直线

Basic Facts about Perpendicular Lines ::关于直直直线的概况

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源