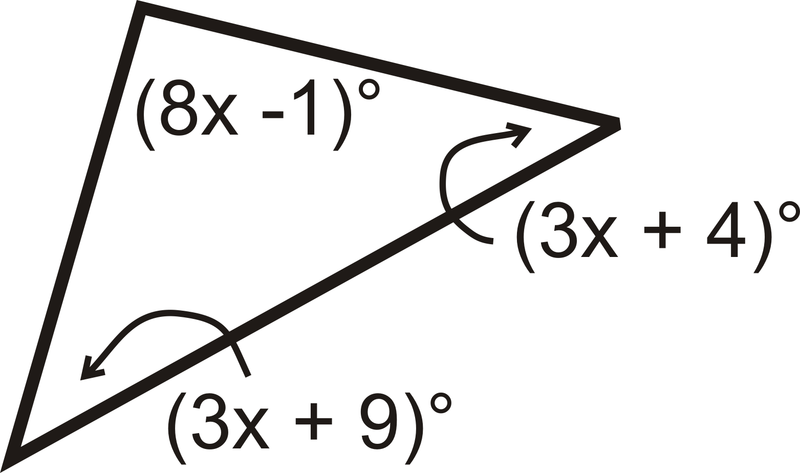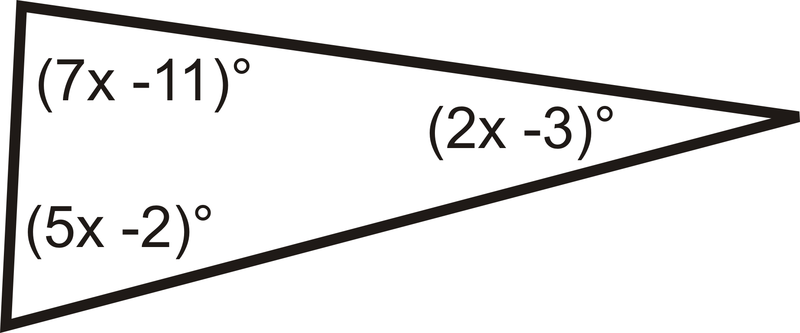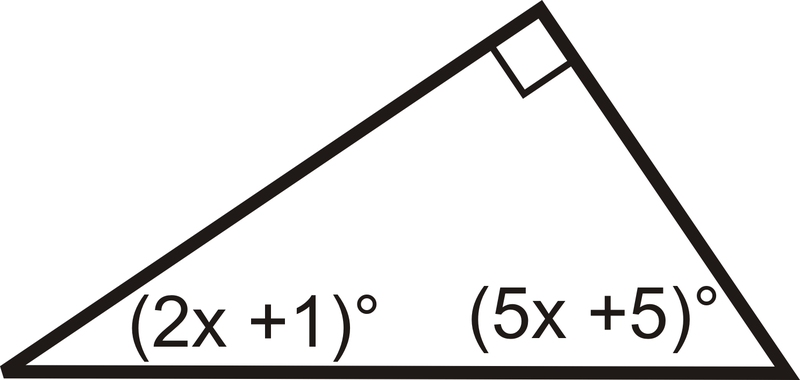4.1 三角定理
章节大纲
-
Triangle Sum Theorem
::三角三角间苏门神话The Triangle Sum Theorem says that the three interior angles of any triangle add up to .
::三角形Sumorem表示,任何三角形的三个内角加起来等于180。.
::m1+m%2+m%3=180%。Here is one proof of the Triangle Sum Theorem.
::这是三角定理的证明Given : with
::以 : @ ABC 与 ADBC 的Prove :
::证明: m1+m2+m3=180Statement Reason 1. with Given 2. Theorem 3. angles have = measures 4. Linear Pair Postulate 5. Angle Addition Postulate 6. Substitution PoE 7. Substitution PoE You can use the Triangle Sum Theorem to find missing angles in triangles.
::您可以使用三角 Sum 理论在三角形中找到缺失的角度 。What if you knew that two of the angles in a triangle measured ? How could you find the measure of the third angle?
::如果你知道一个三角形中两个角度是55°C的呢?你如何找到第三个角度的度量?Examples
::实例Example 1
::例1Two interior angles of a triangle measure and . What is the third interior angle of the triangle?
::三角度为 50 和 70 的两个内角。 三角度的第三个内角是什么 ?.
::50 70x=180 。Solve this equation and you find that the third angle is .
::解决这个方程式,你就会发现第三个角度是60Example 2
::例2Find the value of and the measure of each angle.
::查找 x 的值和每个角度的度量。All the angles add up to .
::所有角度加起来等于180
:8x- 1) ( 3x+9) ( 3x+4) ( 3x+4) ( 14x+12) ( 14x+12) ( 180) ( 14x) ( 14x) ( 14x) = 168x=12)
Substitute in 12 for to find each angle.
::以 12 代替 x 查找每个角度 。Example 3
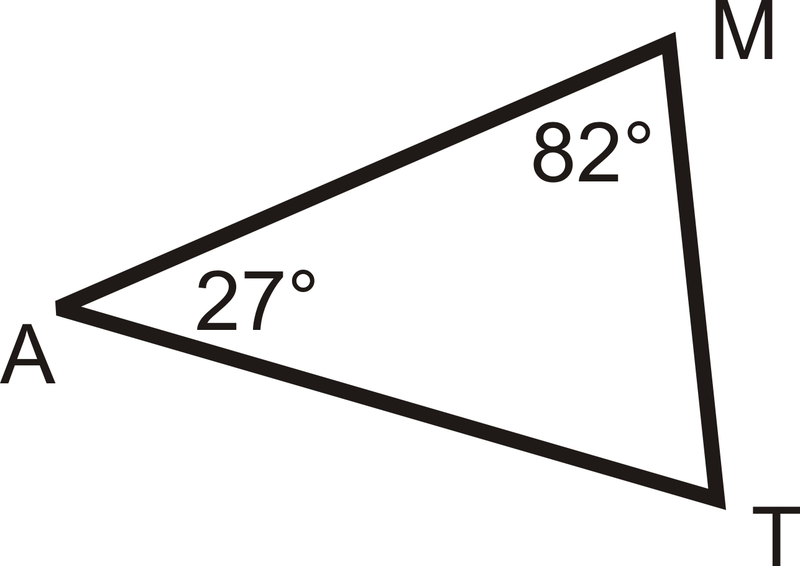
::例3What is ?
::什么是MT?We know that the three angles in the triangle must add up to . To solve this problem, set up an equation and substitute in the information you know.
::我们知道三角形中的三个角度必须相加到 180 。 要解决这个问题, 请设置一个方程, 并替换您所知道的信息 。
::M+mA+mT=1808227MT=180109MT=180MT=71Example 4
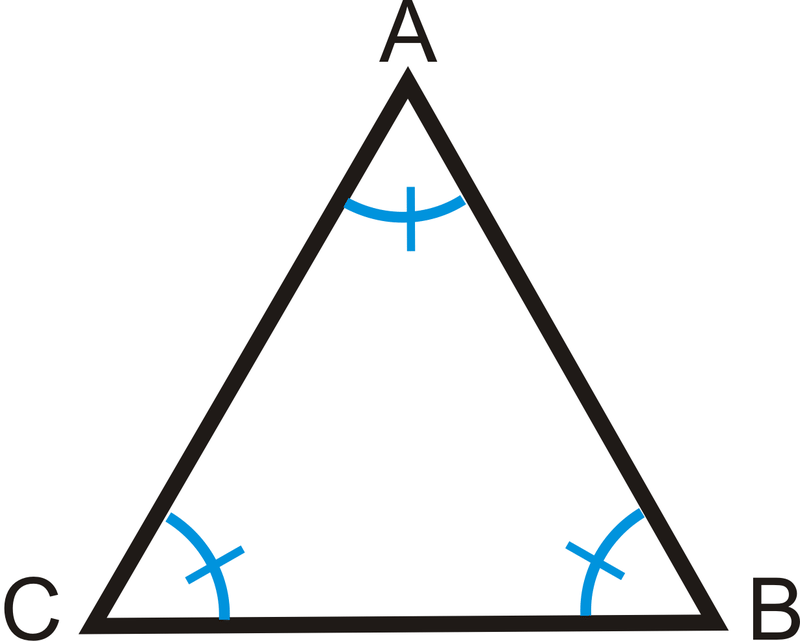
::例4What is the measure of each angle in an equiangular triangle ?
::方形三角形中每个角度的度量是多少?To solve, remember that is an equiangular triangle, so all three angles are equal. Write an equation.
::要解析, 请记住 { ABC 是一个等角三角形, 所以所有三个角度都是相等的。 写入一个公式 。
::mA+mB+mC=180mA+mA+mA=180Substitutive, 所有角度都等于3mA=180Combine like terms.mA=60If , then and .
::如果mA=60,那么mB=60和mC=60。Each angle in an equiangular triangle is .
::角角三角形的每个角是60。Example 5
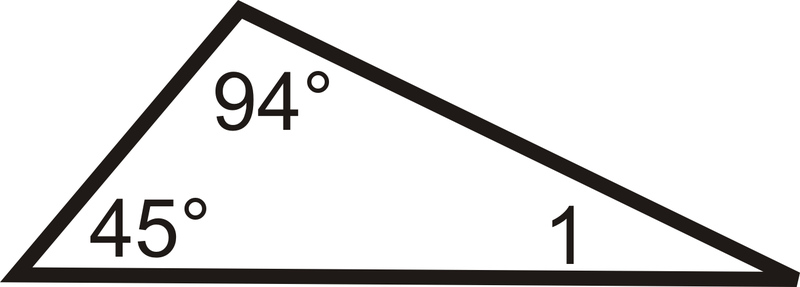
::例5Find the measure of the missing angle.
::查找缺失角度的度量 。We know that and because it is a right angle . Set up an equation like in Example 3.
::我们知道 mO=41和 mG=90, 因为它是一个正确的角度。 设置一个像例3那样的方程 。
::mD+mO+mG=180mD+4190180MD+4190MD+4190MD=49Review
::回顾Determine in each triangle.
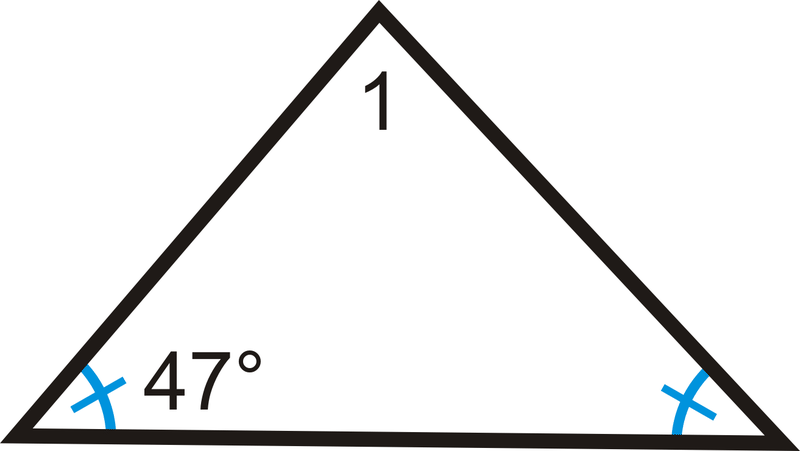
::在每个三角形中确定 m% 1 。1.
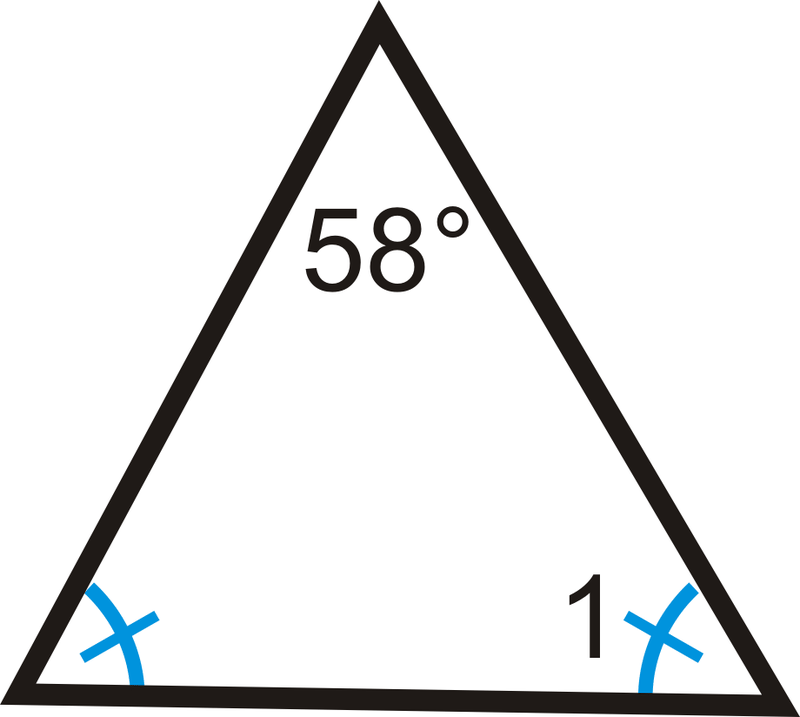
2.
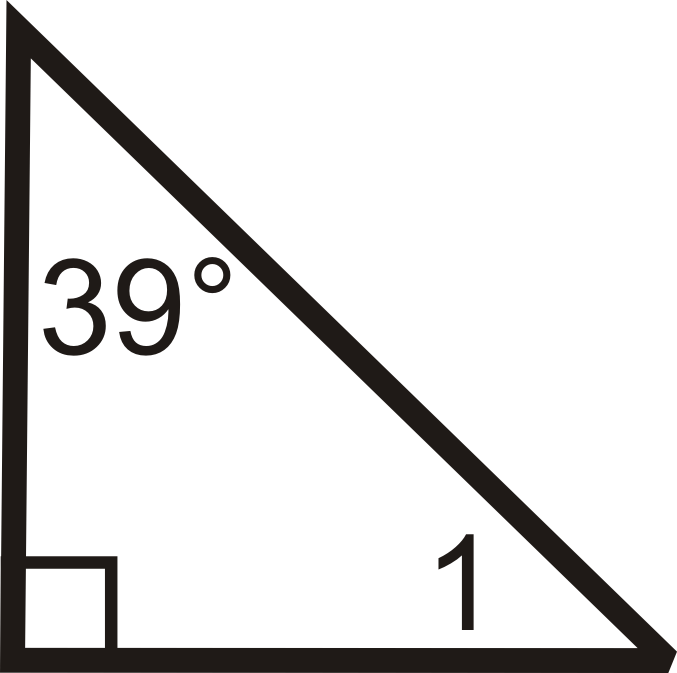
3.
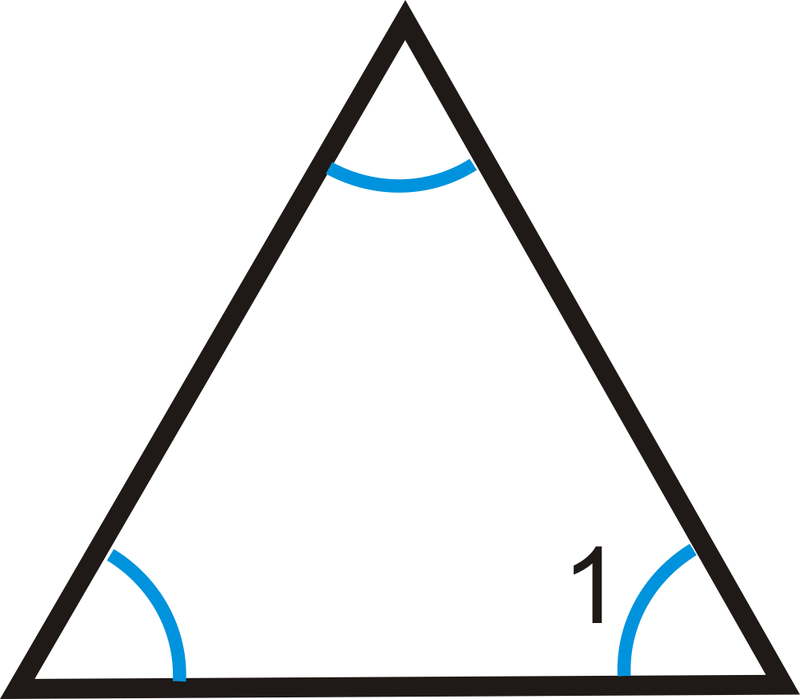
4.
5.
6.
7.
8. Two interior angles of a triangle measure and . What is the third interior angle of the triangle?
::8. 三角度为32°和64°的两个内角。三角度的第三个内角是什么?9. Two interior angles of a triangle measure and . What is the third interior angle of the triangle?
::9. 三角形措施111和12的两个内角。三角形第三个内角是什么?10. Two interior angles of a triangle measure and . What is the third interior angle of the triangle?
::10. 三角度量 2 和 157 的两个内角。三角度量 2 和 157 的第三个内角是什么?Find the value of and the measure of each angle.
::查找 x 的值和每个角度的度量。11.
12.
13.
14.
15.
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。Resources
::资源