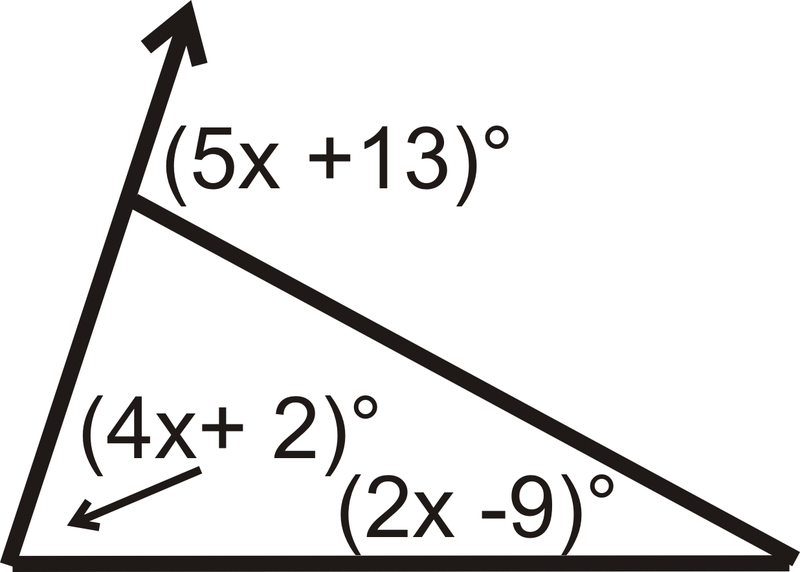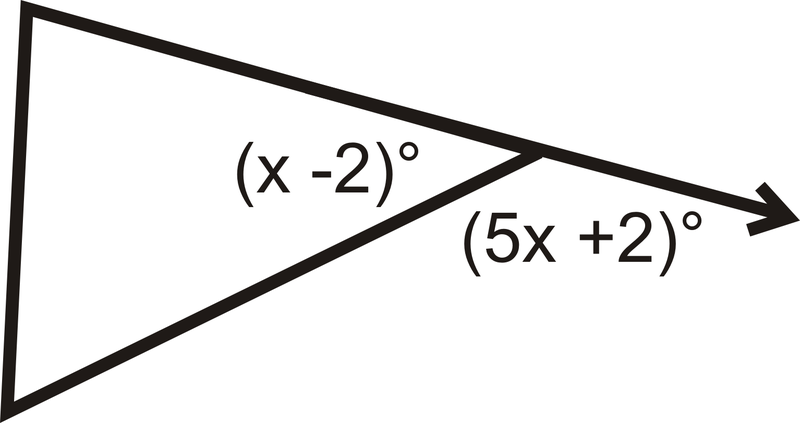4.2 外部外角定理

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 外部外角定理

  Collapse Expand

  外部外角定理

  播放段落

  Exterior Angles
  ::外外角

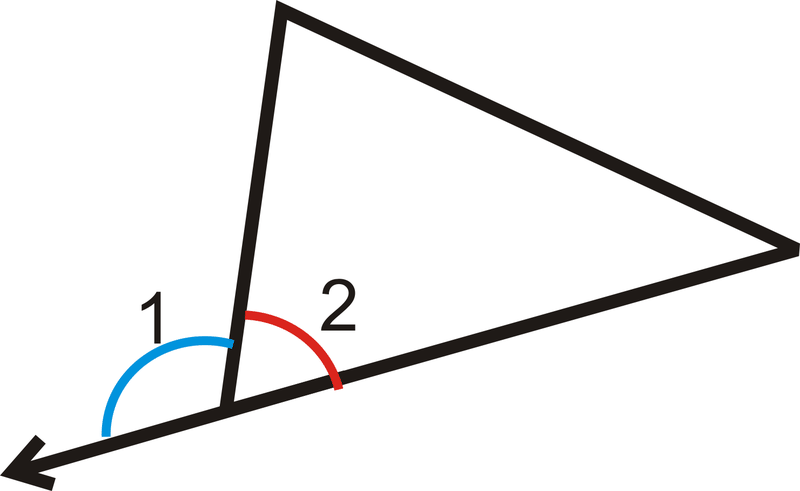
  播放段落

  An Exterior Angle is the angle formed by one side of a polygon and the extension of the adjacent side.
  ::外角是指多边形一面形成的角度和相邻侧的延伸。

  播放段落

  In all polygons, there are two sets of exterior angles, one that goes around clockwise and the other goes around counterclockwise.
  ::在所有多边形中,有两组外向角度,一组按时运行,另一组按时运行。

  

  播放段落

  Notice that the interior angle and its adjacent exterior angle form a linear pair and add up to $\begin{align*}180^\circ\end{align*}$ .
  ::注意内角及其相邻外部角形成线性对配,加起来等于180。

  播放段落

  $$\begin{align*}m\angle1 + m\angle2 = 180^\circ\end{align*}$$
  ::m1+m2=180

  

  播放段落

  There are two important theorems to know involving exterior angles: the Exterior Angle Sum Theorem and the Exterior Angle Theorem .
  ::有两个重要理论需要了解,其中涉及外部角度:外角集合理论和外角定理。

  播放段落

  The Exterior Angle Sum Theorem states that the exterior angles of any polygon will always add up to $\begin{align*}360^\circ\end{align*}$ .
  ::外部角集合理论指出,任何多边形的外部角总和为360。

  

  播放段落

  $$\begin{align*}m\angle{1} + m\angle{2}+m\angle{3} &= 360^\circ\\ m\angle{4} + m\angle{5} + m\angle{6} & = 360^\circ\end{align*}$$ .
  ::m1+m%2+m3=360@m4+m5+m6=360。

  播放段落

  The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of its remote interior angles . ( Remote Interior Angles are the two interior angles in a triangle that are not adjacent to the indicated exterior angle.)
  ::外角 外角 外角 表示三角形的外角等于其边远内角的总和 。 (远程内角是三角形中与指定外角不相邻的两个内角 。)

  

  播放段落

  $$\begin{align*}m\angle{A} + m\angle{B}=m\angle{ACD}\end{align*}$$
  ::mA+mB=mACD( mA+mB=mACD)

  播放段落

  What if you knew that two of the exterior angles of a triangle measured $\begin{align*}130^\circ\end{align*}$ ? How could you find the measure of the third exterior angle?
  ::如果你知道一个三角形的两个外角是130°C,你如何找到第三个外角的尺寸?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Two interior angles of a triangle are $\begin{align*}40^\circ\end{align*}$ and $\begin{align*}73^\circ\end{align*}$ . What are the measures of the three exterior angles of the triangle?
  ::三角形的两个内角是 40 和 73 。 三角形的三个外角的度量是多少 ?

  播放段落

  Remember that every interior angle forms a linear pair (adds up to $\begin{align*}180^\circ\end{align*}$ ) with an exterior angle. So, since one of the interior angles is $\begin{align*}40^\circ\end{align*}$ that means that one of the exterior angles is $\begin{align*}140^\circ\end{align*}$ (because $\begin{align*}40+140=180\end{align*}$ ). Similarly, since another one of the interior angles is $\begin{align*}73^\circ\end{align*}$ , one of the exterior angles must be $\begin{align*}107^\circ\end{align*}$ . The third interior angle is not given to us, but we could figure it out using the Triangle Sum Theorem. We can also use the Exterior Angle Sum Theorem. If two of the exterior angles are $\begin{align*}140^\circ\end{align*}$ and $\begin{align*}107^\circ\end{align*}$ , then the third Exterior Angle must be $\begin{align*}113^\circ\end{align*}$ since $\begin{align*}140+107+113=360\end{align*}$ .
  ::记住每个内角都形成直线对( 添加到 180 ) 外角。 因此, 由于内部角之一是 40 , 这意味着外角之一是 140 ( 代表 40+140=180 ) 。 同样, 由于内部角中的另一个是 73 , 外角必须是 107 。 第三个内角没有给我们, 但是我们可以使用三角形 Sum 理论来找出它。 我们还可以使用 Exfore Angle Sum Theorem 。 如果两个外角是 140 和 107 , 那么第三个外角必须是 113 , 因为 140+107+113=360 。

  播放段落

  So, the measures of the three exterior angles are $\begin{align*}140\end{align*}$ , $\begin{align*}107\end{align*}$ and $\begin{align*}113\end{align*}$ .
  ::因此,三个外角的度量是140、107和113。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the value of $\begin{align*}x\end{align*}$ and the measure of each angle.
  ::查找 x 的值和每个角度的度量。

  

  播放段落

  Set up an equation using the Exterior Angle Theorem.
  ::使用外部角定理设置方程式 。

  播放段落

  $$\begin{align*}&(4x+2)^\circ + (2x-9)^\circ = (5x+13)^\circ\\ & \quad \uparrow \qquad \qquad \nearrow \qquad \qquad \qquad \uparrow\\ & \text{remote interior angles} \qquad \qquad \text{exterior angle}\\ & \qquad \qquad \quad \ (6x-7)^\circ = (5x+13)^\circ\\ & \qquad \qquad \qquad \qquad \ \ x = 20\end{align*}$$
  :4x+2) (2x-9) (5x+13) (6x-7) (5x+13) x=20)

  播放段落

  Substitute in $\begin{align*}20\end{align*}$ for $\begin{align*}x\end{align*}$ to find each angle.
  ::以 20 x 代替 x 找到每个角度 。

  播放段落

  $$\begin{align*}[4(20)+2]^\circ=82^\circ && [2(20)-9]^\circ=31^\circ && \text{Exterior angle:} \ [5(20)+13]^\circ=113^\circ\end{align*}$$
  ::[(20)+2) 82[2(20)-(9)] 31外部角度: [5(20)+13] 113

  播放段落

  Example 3
  ::例3

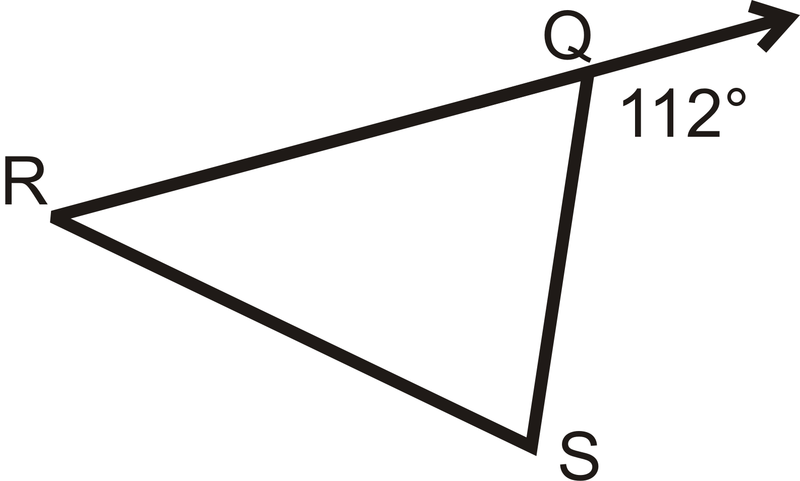
  播放段落

  Find the measure of $\begin{align*}\angle{RQS}\end{align*}$ .
  ::查找 QQS 的量度 。

  

  播放段落

  Notice that $\begin{align*}112^\circ\end{align*}$ is an exterior angle of $\begin{align*}\triangle{RQS}\end{align*}$ and is supplementary to $\begin{align*}\angle{RQS}\end{align*}$ .
  ::请注意112是RQS的外部角度,是对RQS的补充。

  播放段落

  Set up an equation to solve for the missing angle.
  ::设置一个方程式, 以解析缺失角度 。

  播放段落

  $$\begin{align*}112^\circ + m\angle{RQS} & = 180^\circ\\ m\angle{RQS} &= 68^\circ\end{align*}$$
  ::112RQS=180mRQS=68

  播放段落

  Example 4
  ::例4

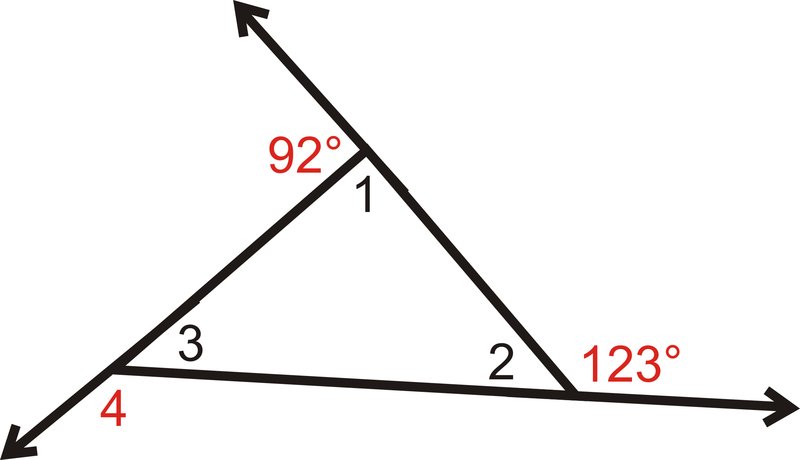
  播放段落

  Find the measures of the numbered interior and exterior angles in the triangle.
  ::查找三角形中编号的内外角的度量。

  

  播放段落

  We know that $\begin{align*}m\angle{1} + 92^\circ = 180^\circ\end{align*}$ because they form a linear pair. So, $\begin{align*}m\angle{1} = 88^\circ\end{align*}$ .
  ::我们知道 m1+92180 因为它们形成线性对。所以, m1=88。

  播放段落

  Similarly, $\begin{align*}m\angle{2} + 123^\circ = 180^\circ\end{align*}$ because they form a linear pair. So, $\begin{align*}m\angle{2} = 57^\circ\end{align*}$ .
  ::同样, m2+123180 因为它们形成线性对。 m2=57。

  播放段落

  We also know that the three interior angles must add up to $\begin{align*}180^\circ\end{align*}$ by the Triangle Sum Theorem.
  ::我们还知道,三角三角理论的 三个内部角度必须加起来 高达180。

  播放段落

  $$\begin{align*}m\angle{1} + m\angle{2} +m\angle{3} & = 180^\circ \qquad \text{by the Triangle Sum Theorem.}\\ 88^\circ + 57^\circ + m\angle{3} &= 180\\ m\angle{3} & = 35^\circ\end{align*}$$
  ::m1+m2+m3=180在三角形的理论上。 8857m3=18003=35

  播放段落

  $$\begin{align*}\text{Lastly}, \ m\angle{3} + m\angle{4} & = 180^\circ \qquad \text{because they form a linear pair}.\\ 35^\circ + m\angle{4} &= 180^\circ\\ m\angle{4} &= 145^\circ\end{align*}$$
  ::最后, m3+m4=180 因为他们组成了直线配对 354=180m4=14545

  播放段落

  Example 5
  ::例5

  播放段落

  What is the value of $\begin{align*}p\end{align*}$ in the triangle below?
  ::P在下面三角形中的值是多少?

  

  播放段落

  First, we need to find the missing exterior angle, which we will call $\begin{align*}x\end{align*}$ . Set up an equation using the Exterior Angle Sum Theorem.
  ::首先,我们需要找到缺失的外部角度, 也就是我们称之为 x。 使用 Exeign Angle Sum Theorem 设置一个方程 。

  播放段落

  $$\begin{align*}130^\circ + 110^\circ + x &= 360^\circ\\ x& = 360^\circ-130^\circ-110^\circ\\ x& = 120^\circ\end{align*}$$
  ::130 110 x=360 x=360 130 110 x=120

  播放段落

  $\begin{align*}x\end{align*}$ and $\begin{align*}p\end{align*}$ add up to $\begin{align*}180^\circ\end{align*}$ because they are a linear pair.
  ::x和p加起来等于180,因为它们是线性对。

  播放段落

  $$\begin{align*}x + p & = 180^\circ\\ 120^\circ + p & = 180^\circ\\ p & = 60^\circ\end{align*}$$
  ::xp=180120p=180p=60

  播放段落

  Review
  ::回顾

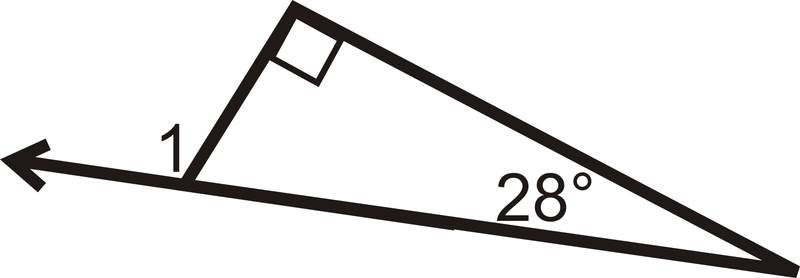
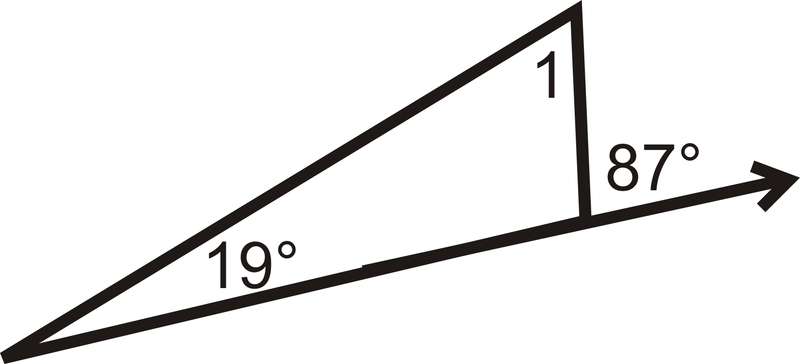
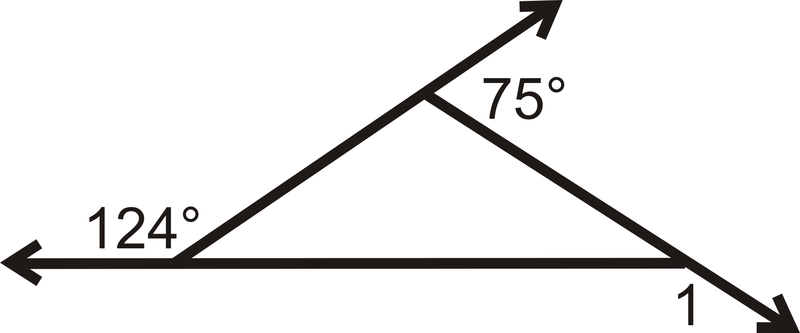
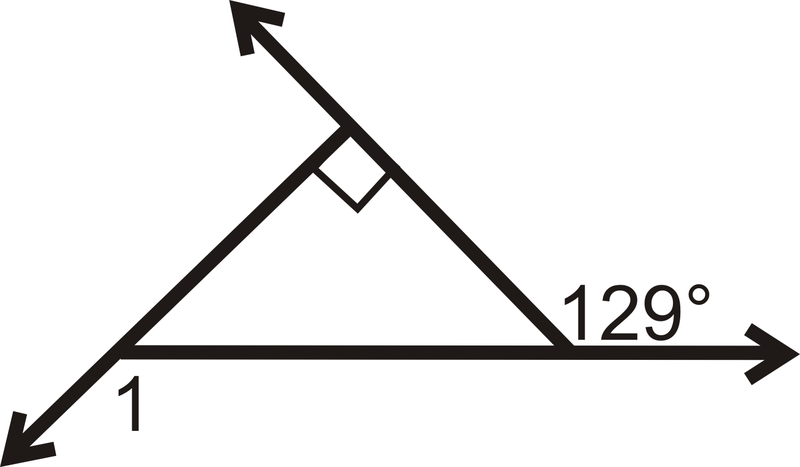
  播放段落

  Determine $\begin{align*}m\angle{1}\end{align*}$ .
  ::确定 m% 1 。

  1. 
  2. 
  3. 
  4. 
  5. 
  6. 

  播放段落

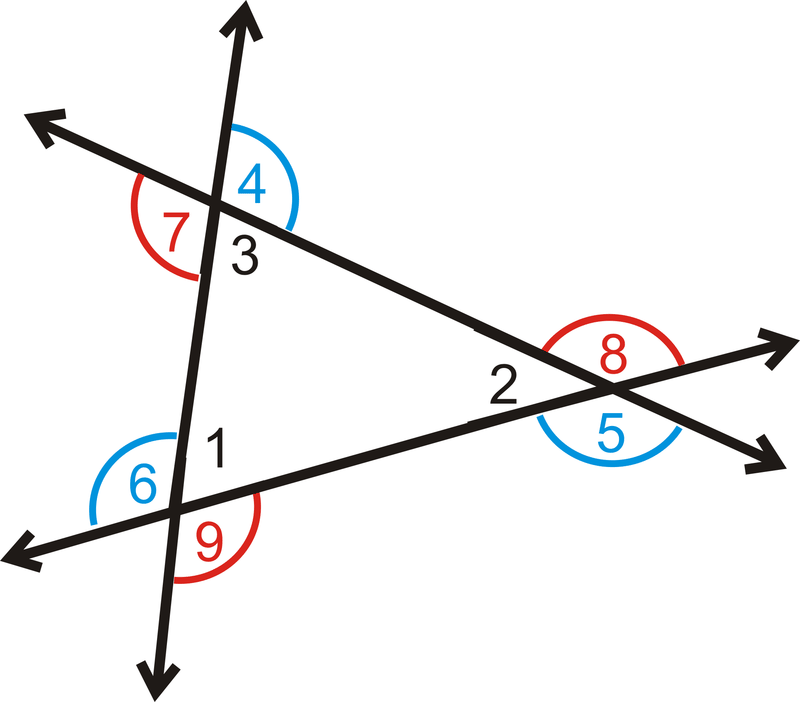
  Use the following picture for the next three problems:
  ::下三个问题使用以下图片 :

  播放段落
  7. What is $\begin{align*}m\angle{1}+m\angle{2}+m\angle{3}\end{align*}$ ?
     ::m1+m2+m3是什么?
  播放段落
  8. What is $\begin{align*}m\angle{4}+m\angle{5}+m\angle{6}\end{align*}$ ?
     ::什么是 m4+m5+m6?
  播放段落
  9. What is $\begin{align*}m\angle{7}+m\angle{8}+m\angle{9}\end{align*}$ ?
     ::7+m8+m9是什么?

  播放段落

  Solve for $\begin{align*}x\end{align*}$ .
  ::解决x。

  10. 
  11. 
  12. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源