Course: 4.5 第三个角定理

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 第三角定理

Collapse Expand
第三角定理
Third Angle Theorem
::第三角定理

If two angles in one triangle are congruent to two angles in another triangle, then the third pair of angles must also congruent. This is called the Third Angle Theorem .
::如果一个三角形中的两个角度与另一个三角形中的两个角度一致,那么第三对角度也必须一致。这叫做第三个角理论。

If $\begin{align*}\angle{A} \cong \angle{D}\end{align*}$ and $\begin{align*}\angle{B} \cong \angle{E}\end{align*}$ , then $\begin{align*}\angle{C} \cong \angle{F}\end{align*}$ .
::如果"A"D和"B"E,那么"C"F。

What if you were given $\begin{align*}\triangle FGH\end{align*}$ and $\begin{align*}\triangle XYZ\end{align*}$ and you were told that $\begin{align*}\angle{F} \cong \angle{X}\end{align*}$ and $\begin{align*}\angle{G} \cong \angle{Y}\end{align*}$ ? What conclusion could you draw about $\begin{align*}\angle{H}\end{align*}$ and $\begin{align*}\angle{Z}\end{align*}$ ?
::如果给了你"FGH"和"XYZ" 还有"FX"和"GY"?

Examples
::实例

Example 1
::例1

Determine the measure of all the angles in each triangle.
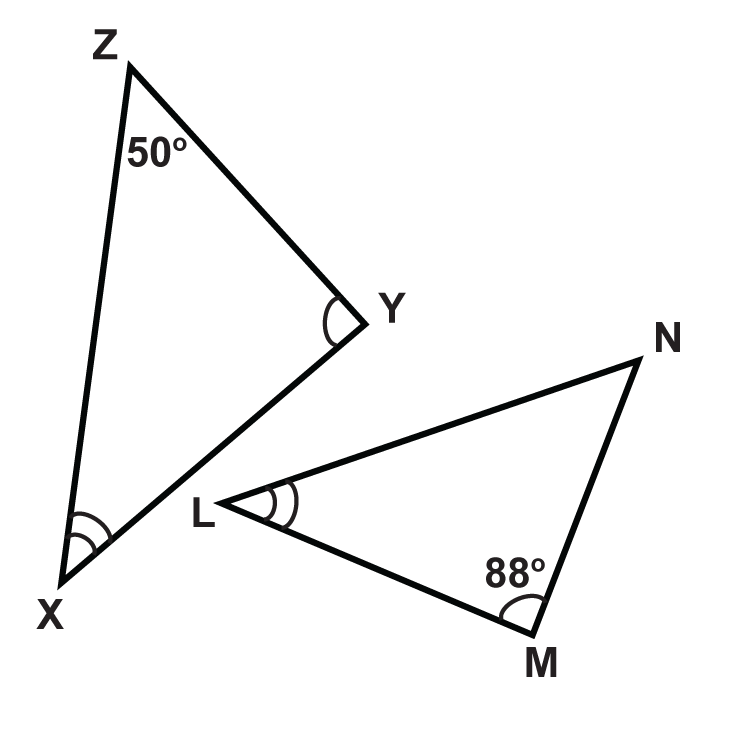
::确定每个三角形中所有角度的度量。

$\begin{align*} m \angle C = m \angle A=m \angle Y=m \angle Z =35\end{align*}$ . By the Triangle Sum Theorem $\begin{align*} m\angle B= m \angle X =110\end{align*}$ .
::MC=mC=mA=mY=mQ35。在三角形三角形的三角形上,Theoremm=B=mQX=110。

Example 2
::例2

Determine the measure of all the angles in each triangle.
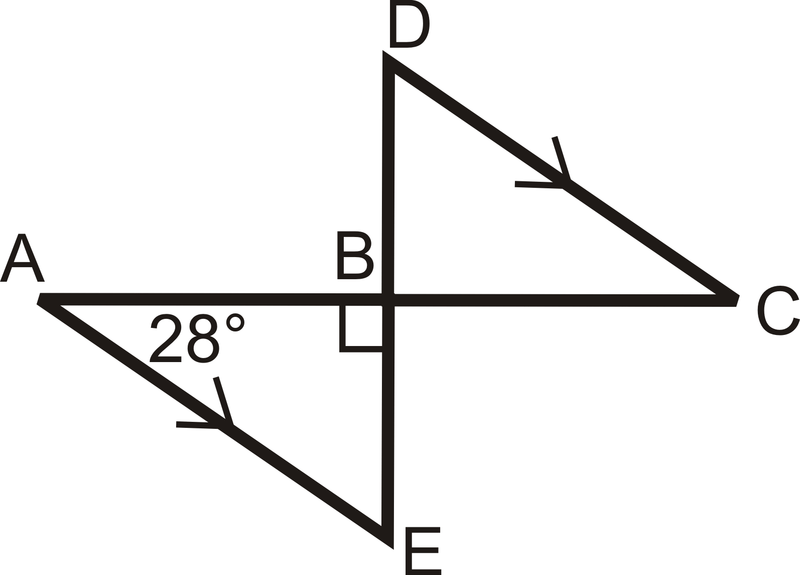
::确定每个三角形中所有角度的度量。

$\begin{align*} m \angle A=28\end{align*}$ , $\begin{align*}m \angle ABE = 90\end{align*}$ and by the Triangle Sum Theorem, $\begin{align*}m \angle E = 62\end{align*}$ . $\begin{align*} m\angle D= m\angle E=62\end{align*}$ because they are and the lines are parallel . $\begin{align*} m\angle C= m\angle A=28\end{align*}$ because they are alternate interior angles and the lines are parallel. $\begin{align*} m \angle DBC = m\angle ABE = 90\end{align*}$ because they are .
::mA=28, mABE=90, 三角形苏莫雷姆为ME=62, mD=mE=62, 因为它们是平行的线条。 mC=mA=28, 因为它们是不同的内部角度, 而线条是平行的。 mDBC=mABE=90, 因为它们是平行的。 mDBC=mABE=90。

Example 3
::例3

Determine the measure of the missing angles.
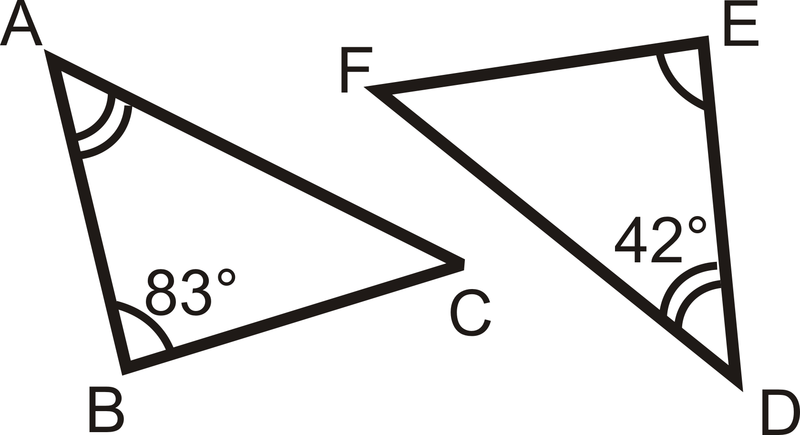
::确定缺失角度的度量。

From the Third Angle Theorem, we know $\begin{align*}\angle{C} \cong \angle{F}\end{align*}$ . From the Triangle Sum Theorem, we know that the sum of the interior angles in each triangle is $\begin{align*}180^\circ\end{align*}$ .
::从第三个角定理中,我们知道“CF”。从三角区定理中,我们知道每个三角区内部角度的总和是180。

$\begin{align*}m\angle{A}+m\angle{B}+m\angle{C}&=180^\circ\\ m\angle{D}+m\angle{B}+m\angle{C}&=180^\circ\\ 42^\circ + 83^\circ+m\angle{C}&=180^\circ\\ m\angle{C}&=55^\circ=m\angle{F}\end{align*}$
::@A+mB+mC=180mD+mB+mC=1804283mC=180mC=55mF

Example 4
::例4

Explain why the Third Angle Theorem works.
::解释为什么第三角定理起作用。

The Third Angle Theorem is really like an extension of the Triangle Sum Theorem. Once you know two angles in a triangle, you automatically know the third because of the Triangle Sum Theorem. This means that if you have two triangles with two pairs of angles congruent between them, when you use the Triangle Sum Theorem on each triangle to come up with the third angle you will get the same answer both times. Therefore, the third pair of angles must also be congruent.
::第三个角定理其实就像三角形 Sum 定理的延伸。一旦您知道三角形中的两个角度, 您就会自动知道第三个角度, 因为三角形的定理。这意味着如果您在三角形上有两个三角形, 两个角的角对齐, 当您在每个三角形上使用三角形的定理来提出第三个角度时, 您就会同时得到相同的答案。因此, 第三对角也必须是相同的。

Example 5
::例5

Determine the measure of all the angles in the triangle:
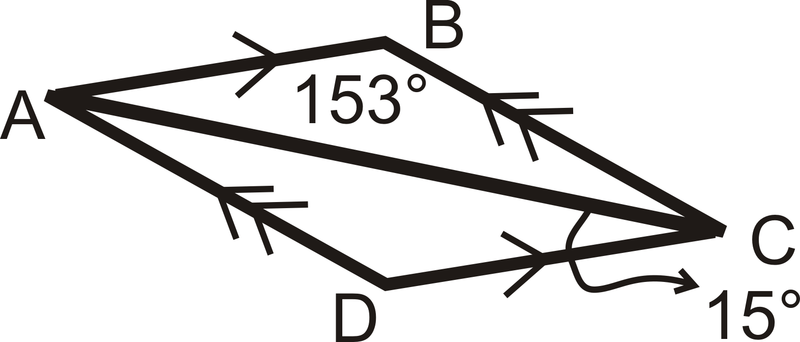
::确定三角形中所有角度的度量 :

First we can see that $\begin{align*} m \angle DCA=15^\circ\end{align*}$ . This means that $\begin{align*}m\angle BAC =15^\circ\end{align*}$ also because they are alternate interior angles. $\begin{align*} m\angle ABC=153^\circ\end{align*}$ was given. This means by the Triangle Sum Theorem that $\begin{align*} m \angle BCA=12^\circ\end{align*}$ . This means that $\begin{align*} m\angle CAD=12^\circ\end{align*}$ also because they are alternate interior angles. Finally, $\begin{align*} m\angle ADC =153^\circ\end{align*}$ by the Triangle Sum Theorem.
::首先,我们可以看到 mDCA=15 。这意味着 mBAC=15 , 也因为它们是其它的内部角度。 mABC=153 被给了。这表示三角区 Sum 论称 mBCA=12 。这意味着 mCA=12 也因为它们是其它的内部角度。最后, mADC=153 被三角区 Sum 论称。

Review
::回顾

Determine the measures of the unknown angles. Angles with similar markings are congruent.
::确定未知角度的度量。带有类似标记的角是相似的。

$\begin{align*}\angle Y\end{align*}$
::# Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y # Y

$\begin{align*}\angle x\end{align*}$
::

$\begin{align*}\angle N\end{align*}$
::N

$\begin{align*}\angle L\end{align*}$
::# L # L # L # L # L # L # L

$\begin{align*}\angle E\end{align*}$
::E

$\begin{align*}\angle F\end{align*}$
::F

$\begin{align*}\angle H\end{align*}$
::~哈 ~ 哈 ~

You may assume that $\begin{align*}\overleftrightarrow{BC} || \overleftrightarrow{HI}\end{align*}$ .
::你可以假设,BCHI。

$\begin{align*}\angle ACB\end{align*}$
::ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB ACB

$\begin{align*}\angle HIJ\end{align*}$
::# 希杰 # # Hij # # Hij # # Hij # # Hij # # Hij # # Hij # # Hij #

$\begin{align*}\angle HJI\end{align*}$
::道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道道

$\begin{align*}\angle IHJ\end{align*}$
::#IHJ# #IHJ# #IHJ# #IHJ# #IHJ# #IHJ# #IHJ #IHJ #IHJ #

$\begin{align*}\angle RQS\end{align*}$
::*RQS* *RQS* *RQS* *RQS* *RQS *RQS* *RQS *RQS *%RQS *RQS* *RQS *RQS *RQS *RQS *RQS *RQQS *RQS *RQS *RQS *RQS *%RQS *RQS *%RQS *RQS *RQS *RQS *RQS *RQS( RQQS QS QS*RQS( RQS QS QS ) 中,%QS

$\begin{align*}\angle SRQ\end{align*}$
::问题

$\begin{align*}\angle TSU\end{align*}$
::

$\begin{align*}\angle TUS\end{align*}$
::

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

第三角定理

Third Angle Theorem ::第三角定理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Third Angle Theorem
::第三角定理

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)