1.9 割裂、割割裂和断裂函数

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section secant 、 Cosecant 和相切函数

  Collapse Expand

  secant 、 Cosecant 和相切函数

  While working to paint your grandfather's staircase, you are looking at the triangular shape made by the wall that support the stairs. The staircase looks like this:

  播放段落

  You are thinking about all of the possible relationships between sides. You already know that there are three common relationships, called sine, cosine, and tangent.
  ::你们正在思考双方可能存在的所有关系。你们已经知道有三种共同的关系,称为正弦、正弦和正弦。

  播放段落

  How many others can you find?
  ::你还能找到多少人?

  播放段落

  Secant, Cosecant and Cotangent Functions
  ::断层、割层和断层函数

  播放段落

  We can define three more functions also based on a right triangle. They are the reciprocals of sine, cosine and tangent.
  ::我们可以根据正确的三角形来定义另外三个函数,它们是正弦、正弦和正弦的对等函数。

  播放段落

  If $\begin{array}{r}\sin A=\frac{a}{c}\end{array}$ , then the definition of cosecant , or $\begin{array}{r}\csc \end{array}$ , is $\begin{array}{r}\csc A=\frac{c}{a}\end{array}$ .
  ::如果sinA=ac,那么Csc 或csc的定义就是cscA=ca。

  播放段落

  If $\begin{array}{r}\cos A=\frac{b}{c}\end{array}$ , then the definition of secant, or $\begin{array}{r}\sec \end{array}$ , is $\begin{array}{r}\sec A=\frac{c}{b}\end{array}$ .
  ::如果cosA=bc,那么分离或秒的定义是seA=cb。

  播放段落

  If $\begin{array}{r}\tan A=\frac{a}{b}\end{array}$ , then the definition of cotangent , or $\begin{array}{r}\cot \end{array}$ , is $\begin{array}{r}\cot A=\frac{b}{a}\end{array}$ .
  ::如果TanA=ab,那么余切物或余切物的定义是cotA=ba。

  播放段落

  Use the definition of secant, cosecant and cotangent to solve the following problems. 
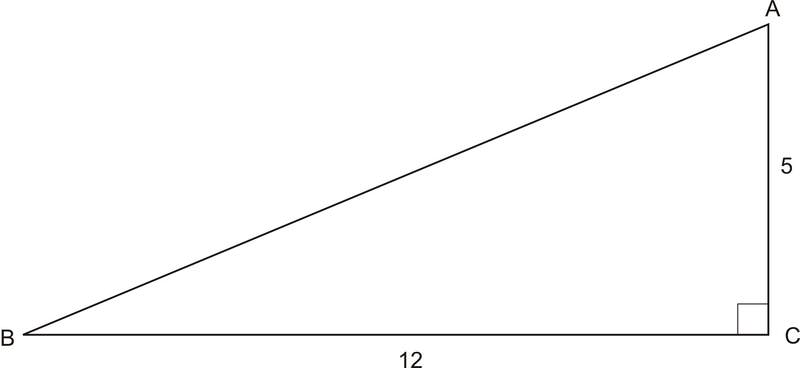
  ::使用割裂、割裂和断裂的定义来解决下列问题。

  播放段落

  1. Find the secant, cosecant, and cotangent of angle $\begin{array}{r}B\end{array}$ .
  ::1. 找出B角的松散、割裂和断裂。

  

   

  播放段落

  First, we must find the length of the hypotenuse. We can do this using the :
  ::首先,我们必须找到下限的长度。我们可以使用以下方法来做到这一点:

  播放段落

  $$\begin{array}{rl}{5}^2+{12}^2& =H^2\\ 25+144& =H^2\\ 169& =H^2\\ H& =13\end{array}$$

  
  ::52+122=H225+144=H2169=H2H=13

  播放段落

  Now we can find the secant, cosecant, and cotangent of angle $\begin{array}{r}B\end{array}$ :
  ::现在,我们可以找到B角的松散、余生和共切:

  播放段落

  $$\begin{array}{rl}\sec B& =\frac{\text{hypotenuse}}{\text{adjacent side}}=\frac{13}{12}\\ \csc B& =\frac{\text{hypotenuse}}{\text{opposite side}}=\frac{13}{5}\\ \cot B& =\frac{\text{adjacent side}}{\text{opposite side}}=\frac{12}{5}\end{array}$$

  
  ::= 1312cscB= 235cotB=相邻侧面=125

  播放段落

  2. Find the secant, cosecant, and cotangent of angle $\begin{array}{r}A\end{array}$
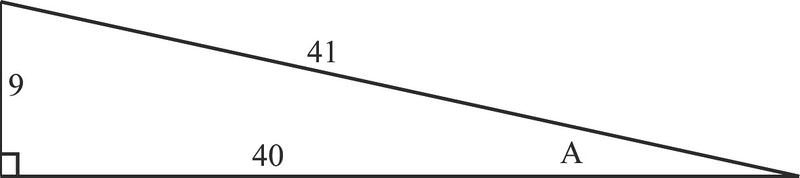
  ::2. 找出A角的松散、割裂和切裂

  

   

  播放段落

  $$\begin{array}{rl}\sec A& =\frac{\text{hypotenuse}}{\text{adjacent side}}=\frac{41}{40}\\ \csc A& =\frac{\text{hypotenuse}}{\text{opposite side}}=\frac{41}{9}\\ \cot A& =\frac{\text{adjacent side}}{\text{opposite side}}=\frac{40}{9}\end{array}$$

  
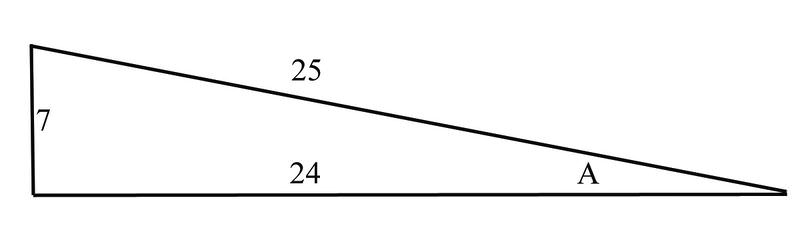
  ::=4,140cscA= 419cotA=邻接侧面=409

  播放段落

  3. Find the sine, cosine, and tangent of angle $\begin{array}{r}A\end{array}$ , and then use this to construct the secant, cosecant, and cotangent of the angle
  ::3. 找到A角的正弦、连弦和正切值,然后用这个来构造角的分离、余切和余切

  

  播放段落

  $$\begin{array}{rl}\sin A& =\frac{\text{opposite side}}{\text{hypotenuse}}=\frac{7}{25}\\ \cos A& =\frac{\text{adjacent side}}{\text{hypotenuse}}=\frac{24}{25}\\ \tan A& =\frac{\text{opposite side}}{\text{adjacent side}}=\frac{7}{24}\end{array}$$

  
  ::A=对面侧对面侧对近侧对面对面侧对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面侧对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面的对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面的对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面的对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面对面

  播放段落

  Since we know that cosecant is the reciprocal of sine, secant is the reciprocal of sine, and cotangent is the reciprocal of tangent, we can construct these functions as follows:
  ::由于我们知道共生是正对的,分生是正对的,分生是正对的,分生是正对的,分生是正对的,因此我们可以将这些职能规定如下:

  播放段落

  $$\begin{array}{rl}\sec A& =\frac{1}{\cos A}=\frac{25}{24}\\ \csc A& =\frac{1}{\sin A}=\frac{25}{7}\\ \cot A& =\frac{1}{\tan A}=\frac{24}{7}\end{array}$$

  
  ::A=2524cscçA=1sinA=257cotA=1tanA=247

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about your grandfather's staircase.
  ::之前,你爷爷的楼梯出了问题

  播放段落

  Looking at a triangle-like the shape of the wall supporting your grandfather's staircase:
  ::看着三角形的墙形 支撑你祖父的楼梯

  

  播放段落

  We can see that there are several ways to make relationships between the sides. In this case, we are only interested in ratios between the sides, which means one side will be divided by another. We've already seen some functions, such as:
  ::我们可以看到,在双方之间建立关系有几种方式。在这种情况下,我们只对双方的比例感兴趣,这意味着一方将被另一方分开。我们已经看到了一些功能,例如:

  播放段落

  1) The side opposite the angle divided by the hypotenuse (the sine function)
  :1) 对面侧面,角除以下限(正弦函数)

  播放段落

  2) The side adjacent the angle divided by the hypotenuse (the cosine function)
  ::2) 相邻的侧面,其角除以下限(余弦函数)

  播放段落

  3) The side opposite the angle divided by adjacent side (the tangent function)
  ::3) 由相邻侧除以的角对面的侧面(相切函数)

  播放段落

  In this section we introduced the reciprocal of the above trig functions. These are found by taking ratios between the same sides shown above, except reversing the numerator and denominator:
  ::在本节中,我们介绍了上述三角函数的对等性。

  播放段落

  4) The hypotenuse divided by the side opposite the angle (the cosecant function)
  ::4) 角对面的侧面除以下限(余生函数)

  播放段落

  5) The hypotenuse divided by the side adjacent to the angle (the secant function)
  ::5) 与角相邻的侧面的下限除以(分离函数)

  播放段落

  6) The adjacent side divided by the opposite side (the cotangent function)
  ::6) 相邻一侧除以对面(余切函数)

  播放段落

  Use the figure below to help solve the following examples.
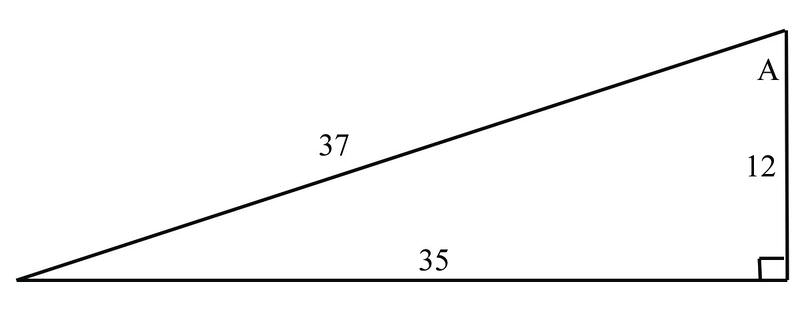
  ::使用下图帮助解决以下实例。

  

  播放段落

  Example 2
  ::例2

  播放段落

  Find the secant $\begin{array}{r}\mathrm{\angle }A\end{array}$
  ::寻找缓存的 A

  播放段落

  The secant function is defined to be $\begin{array}{r}\frac{1}{\cos }\end{array}$ . Since $\begin{array}{r}\cos =\frac{adjacent}{hypotenuse}\end{array}$ , $\begin{array}{r}\sec =\frac{hypotenuse}{adjacent}\end{array}$ .
  ::分离函数定义为 1cos 。 自 cos = 近邻环流, sec = 近邻环流。

  播放段落

  $\begin{array}{r}\sec =\frac{hypotenuse}{adjacent}=\frac{37}{12}\approx 3.08\end{array}$
  ::近地点=3712+3.08

  播放段落

  Example 3
  ::例3

  播放段落

  Find the cosecant of $\begin{array}{r}\mathrm{\angle }A\end{array}$
  ::寻找 A 的余生

  播放段落

  The cosecant function is defined to be $\begin{array}{r}\frac{1}{\sin }\end{array}$ . Since $\begin{array}{r}\sin =\frac{opposite}{hypotenuse}\end{array}$ , $\begin{array}{r}\csc =\frac{hypotenuse}{opposite}\end{array}$ .
  ::COsecant 函数定义为 1sin 。 由于 sin= 超近地点, csc= 超近地点。

  播放段落

  $\begin{array}{r}\csc =\frac{hypotenuse}{opposite}=\frac{37}{35}\approx 1.06\end{array}$
  ::csc = 日光线对面= 37351.06

  播放段落

  Example 4
  ::例4

  播放段落

  Find the cotangent of $\begin{array}{r}\mathrm{\angle }A\end{array}$
  
  ::查找 A 的余切值

  播放段落

   The cotangent function is defined to be $\begin{array}{r}\frac{1}{\tan }\end{array}$ . Since $\begin{array}{r}\tan =\frac{opposite}{adjacent}\end{array}$ , $\begin{array}{r}\cot =\frac{adjacent}{opposite}\end{array}$ .
  ::余切函数定义为 1tan 。 由于 tan= 对面近地点, cot=对面近地点 。

  播放段落

  $\begin{array}{r}\cot =\frac{adjacent}{opposite}=\frac{12}{35}\approx .34\end{array}$
  ::二氧化碳=近地点近地点=123534。

  播放段落

  Review
  ::回顾

  播放段落

  Use the diagram below for questions 1-3.
  ::问题1-3使用下图。

  

  播放段落
  1. Find $\begin{array}{r}\csc A\end{array}$ and $\begin{array}{r}\csc C\end{array}$ .
     ::寻找 cscA 和 cscC 。
  播放段落
  2. Find $\begin{array}{r}\sec A\end{array}$ and $\begin{array}{r}\sec C\end{array}$ .
     ::寻找秒A和秒C。
  播放段落
  3. Find $\begin{array}{r}\cot A\end{array}$ and $\begin{array}{r}\cot C\end{array}$ .
     ::寻找 cotA 和 cotC 。

  播放段落

  Use the diagram to fill in the blanks below.
  ::使用图表填充下面的空白。

  

  播放段落
  4. $\begin{array}{r}\cot A=\frac{?}{?}\end{array}$
     ::A ?
  播放段落
  5. $\begin{array}{r}\csc C=\frac{?}{?}\end{array}$
     ::CSC=C=吗?
  播放段落
  6. $\begin{array}{r}\cot C=\frac{?}{?}\end{array}$
     ::科特・C?
  播放段落
  7. $\begin{array}{r}\sec C=\frac{?}{?}\end{array}$
     ::\ SCQC=? \ \ \ \ \ \ \ \ \ \ \ \ \ \ - - -?
  播放段落
  8. $\begin{array}{r}\csc A=\frac{?}{?}\end{array}$
     ::A=?
  播放段落
  9. $\begin{array}{r}\sec A=\frac{?}{?}\end{array}$
     ::\ \ \ \ \ \ \ \ \ \ \ \ \= \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

  播放段落

  From questions 4-9, we can conclude the following. Fill in the blanks.
  ::从问题4-9,我们可以得出以下结论。填空。

  播放段落
  10. $\begin{array}{r}\sec \underset{\_}{}=\csc A\end{array}$ and $\begin{array}{r}\csc \underset{\_}{}=\sec A\end{array}$ .
      ::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:
  播放段落
  11. $\begin{array}{r}\cot A\end{array}$ and $\begin{array}{r}\cot C\end{array}$ are _________ of each other.
      ::A和C是彼此的一对
  播放段落
  12. Explain why the csc of an angle will always be greater than 1.
      ::解释一个角度的 csc 为何总是大于 1 。
  播放段落
  13. Use your knowledge of 45-45-90 triangles to find the cosecant, secant, and cotangent of a 45 degree angle.
      ::利用你对45 -45 -90三角形的了解 找到45度角的共生、分离和共切。
  播放段落
  14. Use your knowledge of 30-60-90 triangles to find the cosecant, secant, and cotangent of a 30 degree angle.
      ::利用你对30-60-90三角形的了解 找到30度角的共生、分离和共切。
  播放段落
  15. Use your knowledge of 30-60-90 triangles to find the cosecant, secant, and cotangent of a 60 degree angle.
      ::利用你对30-60-90三角形的了解 找到60度角的共生、分离和共切。
  播放段落
  16. As the degree of an angle increases, will the cotangent of the angle increase or decrease? Explain.
      ::随着角度的增加,角的相切度会增减吗?解释一下。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。