4.6 SSS 三角和谐

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section SSS 三角和谐

  Collapse Expand

  SSS 三角和谐

  播放段落

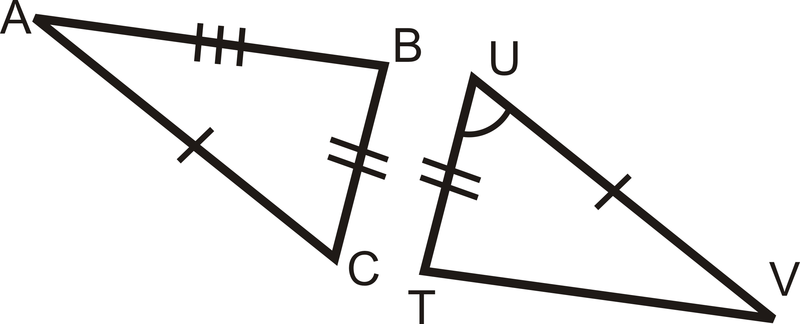
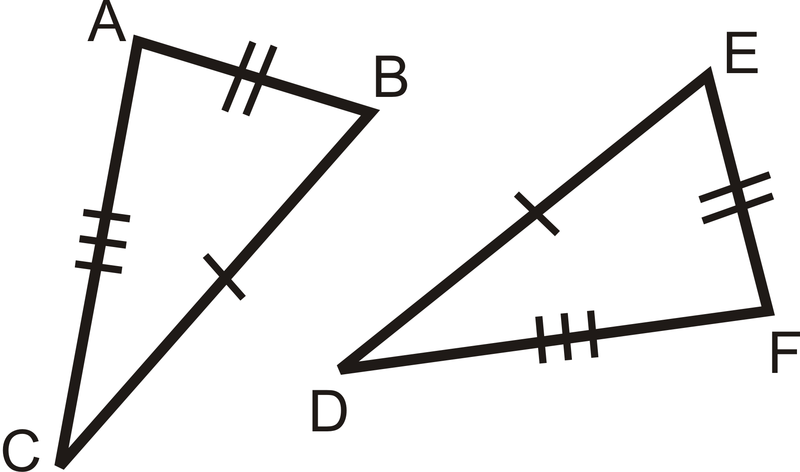
  Side-Side-Side Postulate
  ::侧侧侧侧侧侧侧侧侧侧侧面假设

  播放段落

  If 3 sides in one triangle are congruent to 3 sides in another triangle, then the triangles are congruent.
  ::如果一个三角形的三边与另一个三角形的三边一致,那么三角形是相同的。

  

  播放段落

  $\begin{align*}\overline{BC} \cong \overline{YZ}, \ \overline{AB} \cong \overline{XY}\end{align*}$ , and $\begin{align*}\overline{AC} \cong \overline{XZ}\end{align*}$ then $\begin{align*}\triangle ABC \cong \triangle XYZ\end{align*}$ .
  ::BCZ,ABAXY, ACAXZ,然后AACZ,ABCXYZ。

  播放段落

  This is called the Side-Side-Side (SSS) Postulate and it is a shortcut for proving that two triangles are congruent. Before, you had to show 3 sides and 3 angles in one triangle were congruent to 3 sides and 3 angles in another triangle. Now you only have to show 3 sides in one triangle are congruent to 3 sides in another.
  ::这被称为“ 侧侧侧侧侧( SSS) 假设 ” , 这是用来证明两个三角是相似的捷径。 在之前, 您必须显示一个三角的三边和三个角度与另一个三角的三边和三个角度是相同的。 现在您只需显示一个三角的三边与另一个三角的三边是相同的 。

  播放段落

  What if you were given two triangles and provided with information only about their side lengths? How could you determine if the two triangles were congruent?
  ::假若你们获得两个三角形,而且只获得其侧边长度的信息,你们怎么确定这两个三角形是否一致呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

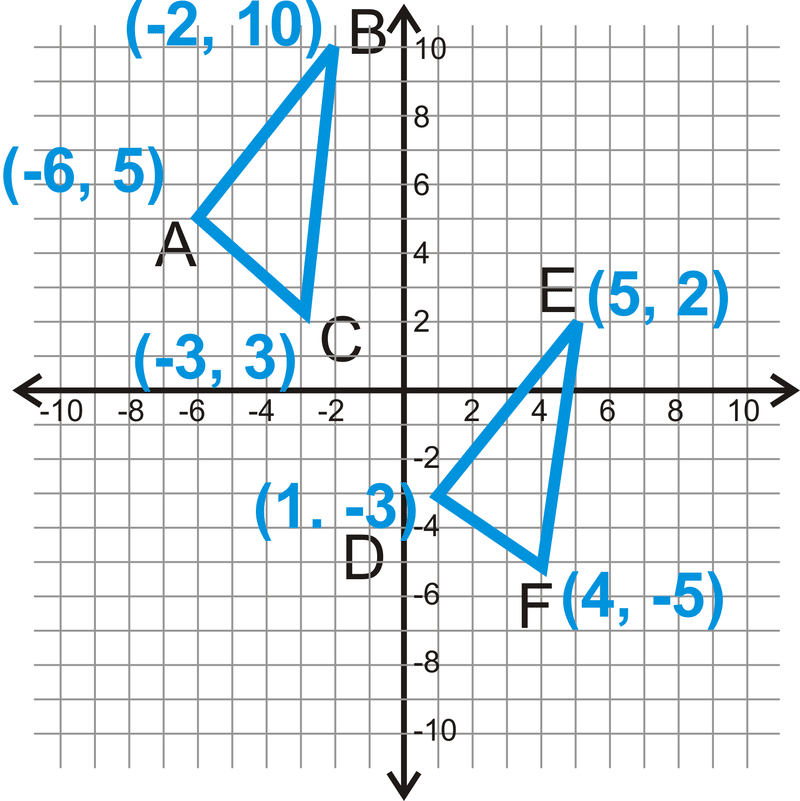
  播放段落

  Determine if the two triangles are congruent.
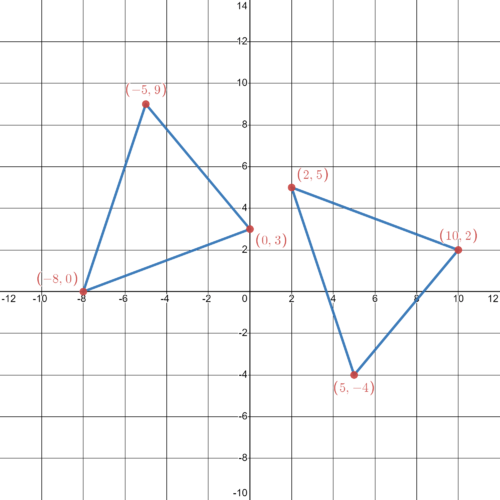
  ::确定两个三角是否一致。

  

  播放段落

  Start with $\begin{align*}\triangle ABC\end{align*}$ .
  ::从ABC开始

  播放段落

  $$\begin{align*}AB & = \sqrt{(-2-(-8))^2+(-2-(-6))^2}\\ & = \sqrt{(6)^2+(4)^2}\\ & = \sqrt{36+16}\\ & = \sqrt{52} = 2\sqrt{13}\end{align*}$$
  ::AB(-2-(-8))2+(-2-(-6))2+(-2-(-6))2+(6)+(4)2}*36+16=52=2/13

  播放段落

  $$\begin{align*}BC & = \sqrt{(-8-(-6))^2+(-6-(-9))^2}\\ & = \sqrt{(-2)^2+(3)^2}\\ & = \sqrt{4+9}\\ & = \sqrt{13}\end{align*}$$
  ::BC*(-8-(-6))2+(-6-(-(9)))2+(-6-(-(9)))2+(-2)2+(3)2+(3)4+9/13

  播放段落

  $$\begin{align*}AC & = \sqrt{(-2-(-6))^2+(-2-(-9))^2}\\ & = \sqrt{(4)^2+(7)^2}\\ & = \sqrt{16+49}\\ & = \sqrt{65}\end{align*}$$
  ::AC(-2-(-6))2+(-2-(-(9)))2+(4)2+(7)2+16+49*65

  播放段落

  Now find the sides of $\begin{align*}\triangle DEF\end{align*}$ .
  ::现在找到ZDEF的两面

  播放段落

  $$\begin{align*}DE & = \sqrt{(3-6)^2 + (9-4)^2}\\ & = \sqrt{(-3)^2 + (5)^2}\\ & = \sqrt{9+25}\\ & = \sqrt{34}\end{align*}$$
  ::DE(3-6)2+(9-4)2+(3)2+(3)2+(5)2+9+2534

  播放段落

  $$\begin{align*}EF & = \sqrt{(6-10)^2+(4-7)^2}\\ & = \sqrt{(-4)^2+(-3)^2}\\ & = \sqrt{16+9}\\ & = \sqrt{25} = 5\end{align*}$$
  ::EF(6-10)2+(4-7)2+(4-7)2+(4)2+(3)2+(3)2+16+9=5

  播放段落

  $$\begin{align*}DF & = \sqrt{(3-10)^2+(9-7)^2}\\ & = \sqrt{(-7)^2+(2)^2}\\ & = \sqrt{49+4}\\ & = \sqrt{53}\end{align*}$$
  ::DF(3-10)2+(9-7)2+(7-7)2+(2)2+49+4*53

  播放段落

  No sides have equal measures, so the triangles are not congruent.
  ::双方没有平等的措施,所以三角形是不一致的。

  播放段落

  Example 2
  ::例2

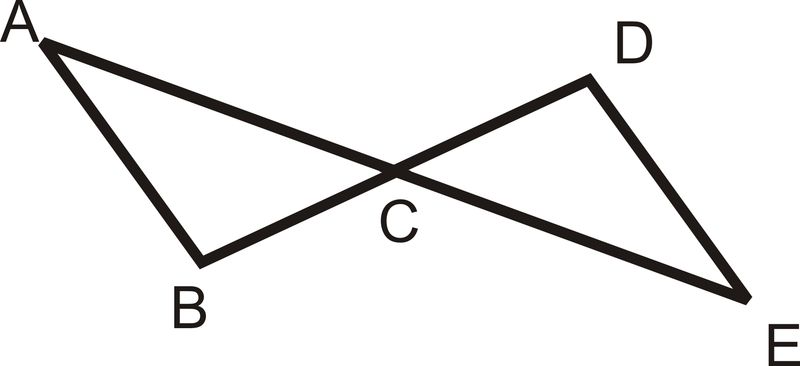
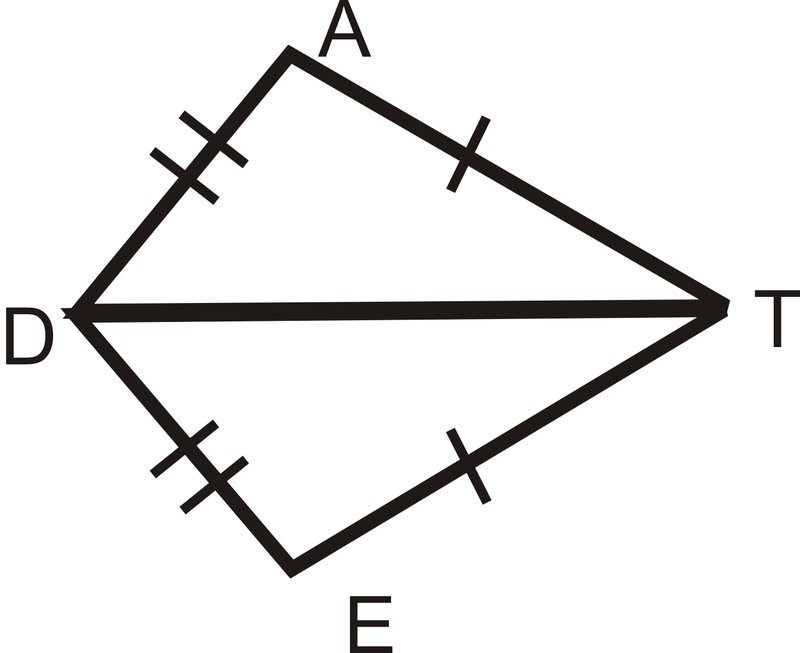
  播放段落

  Fill in the blanks in the proof below.
  ::填充以下证据中的空白。

  播放段落

  Given : $\begin{align*}\overline{AB} \cong \overline{DC}, \ \overline{AC} \cong \overline{DB}\end{align*}$
  ::以: 'AB'D,'AC'DD,'A'DD,'DD,'A'DD,'DD,'A'DD,'A'DD,'A'DD,'DDD,'DD,'DD,'A'DD,'A'DD,'DD,'DD,'A'DD,'DD

  播放段落

  Prove : $\begin{align*}\triangle ABC \cong \triangle DCB\end{align*}$
  ::证明:@ABC_DCB

  

  Statement	Reason
  1.	1.
  2.	2. Reflexive PoC
  3. $\begin{align*}\triangle ABC \cong \triangle DCB\end{align*}$	3.

  Statement	Reason
  1. $\begin{align*}\overline{AB} \cong \overline{DC}, \ \overline{AC} \cong \overline{DB}\end{align*}$	1. Given
  2. $\begin{align*}\overline{BC} \cong \overline{CB}\end{align*}$	2. Reflexive PoC
  3. $\begin{align*}\triangle ABC \cong \triangle DCB\end{align*}$	3. Postulate

  播放段落

  Example 3
  ::例3

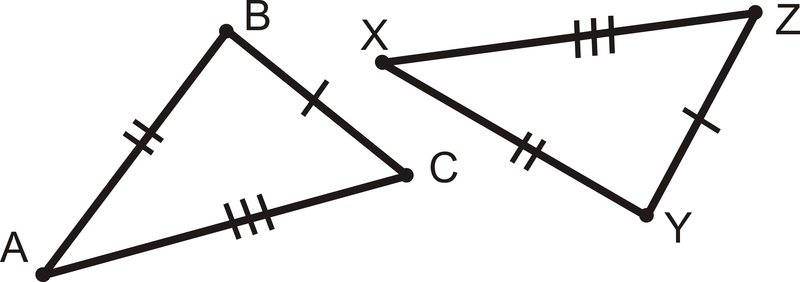
  播放段落

  Write a triangle congruence statement based on the picture below:
  ::根据以下图片写入三角一致语句 :

  

  播放段落

  From the tic marks, we know $\begin{align*}\overline{AB} \cong \overline{LM}, \ \overline{AC} \cong \overline{LK}, \ \overline{BC} \cong \overline{MK}\end{align*}$ . From the SSS Postulate, the triangles are congruent. Lining up the corresponding sides , we have $\begin{align*}\triangle ABC \cong \triangle LMK\end{align*}$ .
  ::从台阶上看,我们知道LM,ACLK,BCK。从SSS的假设看,三角形是相同的。

  播放段落

  Don’t forget ORDER MATTERS when writing . Line up the sides with the same number of tic marks.
  ::写作时不要忘记秩序事项。 以相同数量的微分标记排成两边。

  播放段落

  Example 4
  ::例4

  播放段落

  Write a two-column proof to show that the two triangles are congruent.
  ::写一个两栏证明,以证明这两个三角是相同的。

  

  播放段落

  Given : $\begin{align*}\overline{AB} \cong \overline{DE}\end{align*}$
  ::给:

  播放段落

  $\begin{align*}C\end{align*}$ is the midpoint of $\begin{align*}\overline{AE}\end{align*}$ and $\begin{align*}\overline{DB}\end{align*}$ .
  ::C是AE和DB的中点。

  播放段落

  Prove : $\begin{align*}\triangle ACB \cong \triangle ECD\end{align*}$
  ::证明: ACBECD

  Statement	Reason
  播放段落 1. $\begin{align*}\overline{AB} \cong \overline{DE}\end{align*}$ ::. . . . . 播放段落 $\begin{align*}C\end{align*}$ is the midpoint of $\begin{align*}\overline{AE}\end{align*}$ and $\begin{align*}\overline{DB}\end{align*}$ ::C 是 AE 和 DB 的中点	1.Given
  2. $\begin{align*}\overline{AC} \cong \overline{CE}, \ \overline{BC} \cong \overline{CD}\end{align*}$	2.Definition of a midpoint
  3. $\begin{align*}\triangle ACB \cong \triangle ECD\end{align*}$	3.SSS Postulate

  播放段落

  Note that you must clearly state the three sets of sides are congruent BEFORE stating the triangles are congruent.
  ::请注意,你必须清楚声明三组方是一致的 之前说三角是一致的。

  播放段落

  Example 5
  ::例5

  播放段落

  The only way we will show two triangles are congruent in an $\begin{align*}x-y\end{align*}$ plane is using SSS.
  ::唯一能显示两个三角形的方法 是在X -y平面上 使用SSS

  播放段落

  Find the lengths of all the line segments from both triangles to see if the two triangles are congruent.
  ::查找两个三角形中所有线段的长度, 看看这两个三角形是否一致 。

  播放段落

  To do this, you need to use the distance formula.
  ::要做到这一点,您需要使用距离公式。

  播放段落

  Begin with $\begin{align*}\triangle ABC\end{align*}$ and its sides.
  ::以ABC及其两边开始。

  播放段落

  $$\begin{align*}AB & = \sqrt{(-6-(-2))^2+(5-10)^2}\\ & = \sqrt{(-4)^2+(-5)^2}\\ & = \sqrt{16+25}\\ & = \sqrt{41}\end{align*}$$
  ::AB(-6-(-2))2+(5-10)2+(4)2+(-5)2+(-5)2+(-6-(-2))16+25*41

  播放段落

  $$\begin{align*}BC & = \sqrt{(-2-(-3))^2+(10-3)^2}\\ & = \sqrt{(1)^2+(7)^2}\\ & = \sqrt{1+49}\\ & = \sqrt{50} = 5 \sqrt{2}\end{align*}$$
  ::BC(-2-(-3))2+(10-3)2+(10-3)2(1)2+(7)2+1+49=50=52

  播放段落

  $$\begin{align*}AC & = \sqrt{(-6-(-3))^2 + (5-3)^2}\\ & = \sqrt{(-3)^2+(2)^2}\\ & = \sqrt{9+4}\\ & = \sqrt{13}\end{align*}$$
  ::AC(-6-(-3))2+(-5-3)2(-3)2+(-3)2+(2)2+9+413

  播放段落

  Now, find the lengths of all the sides in $\begin{align*}\triangle DEF\end{align*}$ .
  ::现在,找到ZDEF所有方的长度。

  播放段落

  $$\begin{align*}DE & = \sqrt{(1-5)^2 + (-3-2)^2}\\ & = \sqrt{(-4)^2 + (-5)^2}\\ & = \sqrt{16+25}\\ & = \sqrt{41}\end{align*}$$
  ::DE(1-5)2+(-3-2)2+(-4)2+(-5)2+(-5)2+16+25*41

  播放段落

  $$\begin{align*}EF & = \sqrt{(5-4)^2+(2-(-5))^2}\\ & = \sqrt{(1)^2+(7)^2}\\ & = \sqrt{1+49}\\ & = \sqrt{50} = 5\sqrt{2}\end{align*}$$
  ::EF(5-4)2+(2-(5))2___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________(5-_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  $$\begin{align*}DF & = \sqrt{(1-4)^2+(-3-(-5))^2}\\ & = \sqrt{(-3)^2+(2)^2}\\ & = \sqrt{9+4}\\ & = \sqrt{13}\end{align*}$$
  ::DF(1-4)2+(-3-(-5)5)2(-3)2+(2)2+9+4}13

  播放段落

  $\begin{align*}AB = DE, \ BC = EF\end{align*}$ , and $\begin{align*}AC = DF\end{align*}$ , so the two triangles are congruent by SSS.
  ::AB=DE, BC=EF, AC=DF, 所以两个三角形与 SSS 相似 。

  播放段落

  Review
  ::回顾

  播放段落

  Are the pairs of triangles congruent? If so, write the congruence statement and why.
  ::三角形对齐是否一致? 如果一致,请写一致声明和原因。

  1. 
  2. 
  3. 
  4. 

  播放段落

  State the additional piece of information needed to show that each pair of triangles is congruent.
  ::显示每对三角形的相近性 所需的附加信息 。

  播放段落
  5. Use SSS
     ::使用 SSS
  播放段落
  6. Use SSS
     ::使用 SSS

  播放段落

  Fill in the blanks in the proofs below.
  ::填充以下证据中的空白。

  播放段落
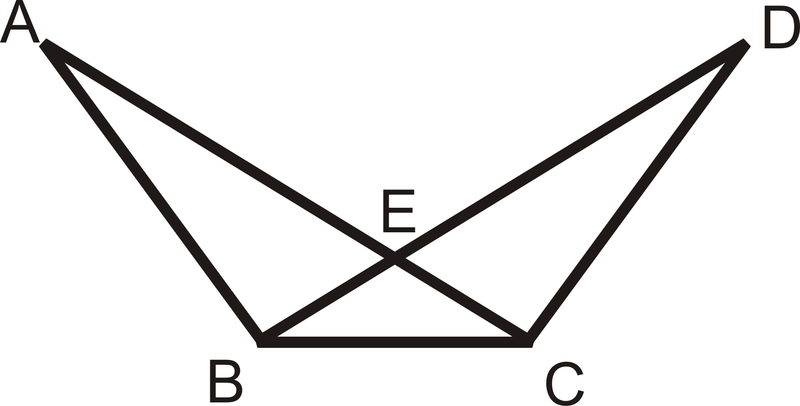
  7. Given : $\begin{align*}B\end{align*}$ is the midpoint of $\begin{align*}\overline{DC}\end{align*}$ $\begin{align*}\overline{AD} \cong \overline{AC}\end{align*}$ Prove : $\begin{align*}\triangle ABD \cong \triangle ABC\end{align*}$
     
     
     ::B是DC'AACprove: 'ABD'ABC的中点

  Statement	Reason
  1.	1.
  2.	2. Definition of a Midpoint
  3.	3. Reflexive PoC
  4. $\begin{align*}\triangle ABD \cong \triangle ABC\end{align*}$	4.

  播放段落

  Find the lengths of the sides of each triangle to see if the two triangles are congruent. Leave your answers under the radical.
  ::查找每个三角形两侧的长度, 看看这两个三角形是否一致。 请将答案放在激进下 。

  8. 
  9. 
  播放段落
  10. $\begin{align*}\triangle ABC: \ A(-1, 5), \ B(-4, 2), \ C(2, -2)\end{align*}$ and $\begin{align*}\triangle DEF: \ D(7, -5), \ E(4, 2), \ F(8, -9)\end{align*}$
      ::ABC:A(-1,5),B(-4,2),C(2,-2)和ZDEF:D(7)-5,E(4),F(8)-9
  播放段落
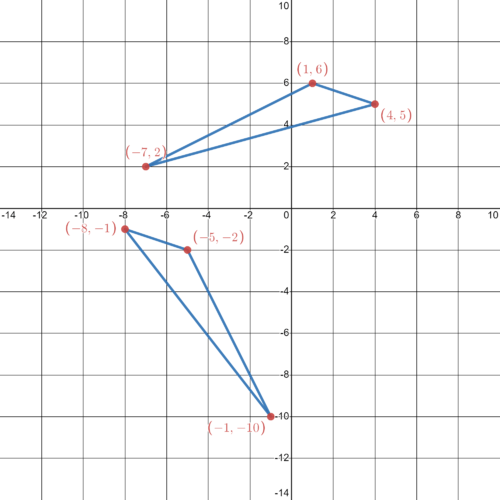
  11. $\begin{align*}\triangle ABC: \ A(-8, -3), \ B(-2, -4), \ C(-5, -9)\end{align*}$ and $\begin{align*}\triangle DEF: \ D(-7, 2), \ E(-1, 3), \ F(-4, 8)\end{align*}$
      ::ABC:A(-8)-3,B(-2)-4,C(-5)-9和Z(DEF):D(-7),E(-1)-1,3,F(-4)-4,8)

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源