1.10 解决右三角的俾塔哥里安理论论

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 解决右三角的毕达哥里安理论

  Collapse Expand

  解决右三角的毕达哥里安理论

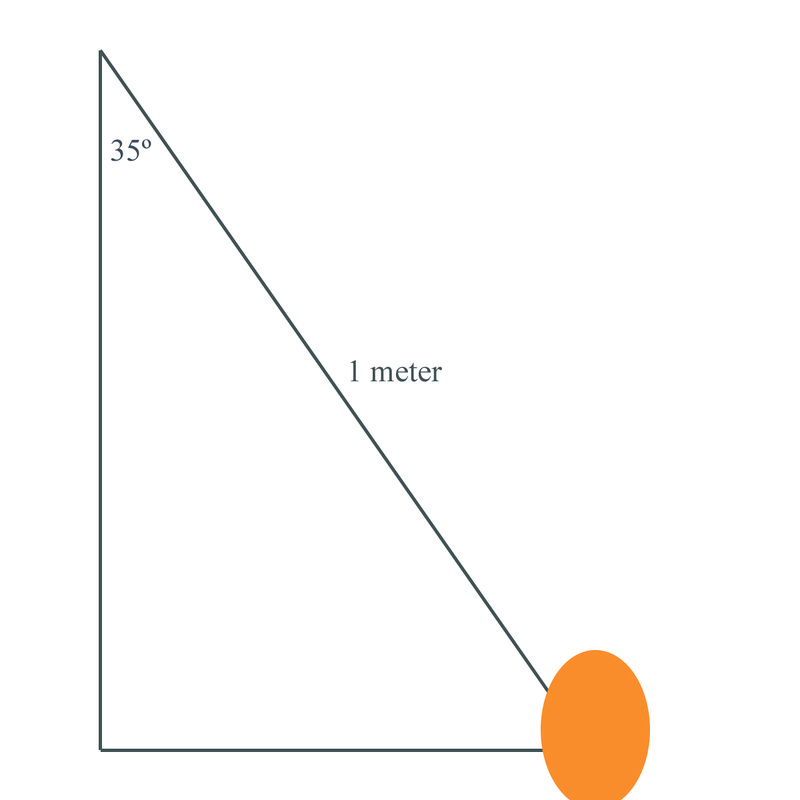
  You are out on the playground with friends playing a game of tetherball. In this game, a ball is attached by a rope to the top of a pole. Each person is trying to hit the ball in a different direction until it wraps the rope completely around the pole. The first person to get the ball wrapped around the pole in their direction is the winner. You can see an example of a tetherball game on the right hand side of the picture shown here:

  播放段落

  You notice that the rope attached to the tetherball is 1 meter long, and that the angle between the rope and the pole is $\begin{array}{r}{35}^{\circ }\end{array}$ degrees. Can you use that information to find out how far the ball is from the pole?
  ::你注意到绳子球的绳子长1米,绳子和杆子之间的角是35°。你能用这些信息来了解球离杆有多远吗?

  播放段落

  Pythagorean Theorem
  ::毕达哥里安神论

  播放段落

  You can use your knowledge of the and the six trigonometric functions to solve a right triangle. Because a right triangle is a triangle with a 90 degree angle, solving a right triangle requires that you find the measures of one or both of the other angles. How you solve for these other angles, as well as the lengths of the triangle's sides, will depend on how much information is given.
  ::您可以使用您对右三角形和六个三角函数的知识来解析右三角形。 因为右三角形是一个三角形,角度为90度, 解析右三角形需要找到其他角度中一个或两个角度的度量。 您如何解析这些其他角度以及三角形边的长度, 将取决于给出的信息量 。

  播放段落

  Let's take a look at some problems involving the Pythagorean Theorem. 
  ::让我们来看看一些 涉及毕达哥伦神话的问题

  播放段落

  1. Solve the triangle shown below.
  ::1. 解决以下三角。

  

   

  播放段落

  We need to find the lengths of all sides and the measures of all angles. In this triangle, two of the three sides are given. We can find the length of the third side using the Pythagorean Theorem:
  ::我们需要找到方形的长度和方形的度量。在这个三角形中,三个方中有两个方形的长度。我们可以用毕达哥伦神话找到第三方的长度:

  播放段落

  $$\begin{array}{rl}{8}^2+b^2& ={10}^2\\ 64+b^2& =100\\ b^2& =36\\ b& =\pm 6\Rightarrow b=6\end{array}$$

  
  ::82+b2=10264+b2=100b2=36b=6*6*b=6

  播放段落

  (You may have also recognized that this is a “Pythagorean Triple,” 6, 8, 10, instead of using the Pythagorean Theorem.)
  :你可能也认识到这是“毕达哥伦三世”,6、8、10,而不是使用毕达哥伦神话。 )

  播放段落

  You can also find the third side using a trigonometric ratio. Notice that the missing side, $\begin{array}{r}b\end{array}$ , is adjacent to $\begin{array}{r}\mathrm{\angle }A\end{array}$ , and the hypotenuse is given. Therefore we can use the cosine function to find the length of $\begin{array}{r}b\end{array}$ :
  ::您也可以使用三角比来找到第三边。 请注意, 缺失的一面 b, 与 A 相邻, 并给出了下限值。 因此, 我们可以使用余弦函数来找到 b 的长度 :

  播放段落

  $$\begin{array}{rl}\cos {53.13}^{\circ }& =\frac{\text{adjacent side}}{\text{hypotenuse}}=\frac{b}{10}\\ 0.6& =\frac{b}{10}\\ b& =0.6(10)=6\end{array}$$

  
  ::相邻的平行日光照射=100.6=b10b=0.6(10)=6

  播放段落

  2. Solve the triangle shown below.
  ::2. 解决以下三角。

  

   

  播放段落

  In this triangle, we need to find the lengths of two sides. We can find the length of one side using a trig ratio. Then we can find the length of the third side by using a trig function with the information given originally and a different trig function. Because the side we found is an approximation , using the Pythagorean Theorem would not yield the most accurate answer for the other missing side. Therefore, we should use a trig function with the original information to find the length of the third side instead. Only use the given information when solving right triangles.
  ::在此三角形中, 我们需要找到两边的长度 。 使用三角比, 我们可以找到一方的长度 。 这样我们就可以通过使用原始信息的三角函数和不同的三角函数来找到第三边的长度 。 因为我们找到的一方是一个近似值, 使用 Pythagoren Theorem 无法为另一方的缺失提供最准确的答案 。 因此, 我们应该使用带有原始信息的三角函数来找到第三边的长度 。 只有解决右三角形时才能使用给定的信息 。

  播放段落

  We are given the measure of $\begin{array}{r}\mathrm{\angle }A\end{array}$ , and the length of the side adjacent to $\begin{array}{r}\mathrm{\angle }A\end{array}$ . If we want to find the length of the hypotenuse, $\begin{array}{r}c\end{array}$ , we can use the cosine ratio:
  ::我们得到了A和A附近边的长度。如果我们想要找到的长度, c, 我们可以使用余弦比 :

  播放段落

  $$\begin{array}{rl}\cos {40}^{\circ }& =\frac{adjacent}{hypotenuse}=\frac{6}{c}\\ \cos {40}^{\circ }& =\frac{6}{c}\\ c\cos {40}^{\circ }& =6\\ c& =\frac{6}{\cos {40}^{\circ }}\approx 7.83\end{array}$$

  
  ::404477.83=6ccos406cccos 406c=6cos40407.83

  播放段落

  If we want to find the length of the other leg of the triangle, we can use the tangent ratio. This will give us the most accurate answer because we are not using approximations.
  ::如果我们想要找到三角形另一条腿的长度, 我们可以使用正切比。 这将给我们提供最准确的答案, 因为我们没有使用近似值 。

  播放段落

  $$\begin{array}{rl}\tan {40}^{\circ }& =\frac{opposite}{adjacent}=\frac{a}{6}\\ a& =6\tan {40}^{\circ }\approx 5.03\end{array}$$

  
  ::40

  播放段落

  3. Solve the triangle shown below.
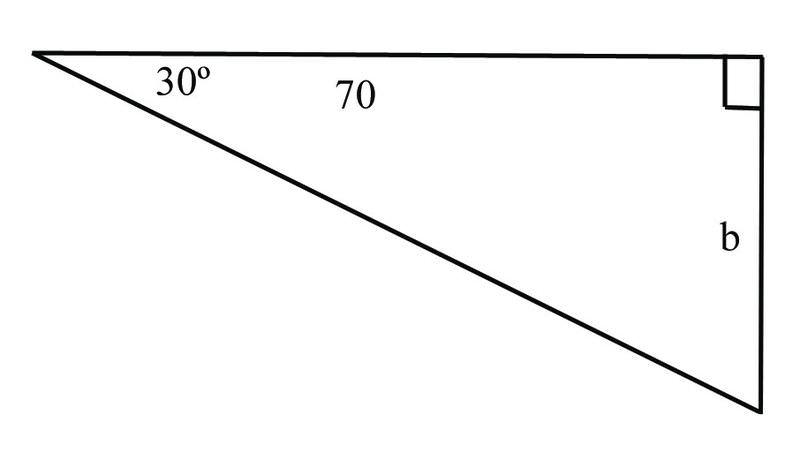
  ::3. 解决以下三角。

  

   

  播放段落

  In this triangle, we have the length of one side and one angle. Therefore, we need to find the length of the other two sides. We can start with a trig function:
  ::在这个三角形中,我们有一个侧面和一个角度的长度。 因此,我们需要找到另外两个侧面的长度。 我们可以从一个三角函数开始:

  播放段落

  $$\begin{array}{rl}\tan {30}^{\circ }& =\frac{opposite}{adjacent}=\frac{b}{7}\\ \tan {30}^{\circ }& =\frac{b}{7}\\ 7\tan {30}^{\circ }& =b\\ b& =7\tan {30}^{\circ }\approx 4.04\end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}30 -30 -404 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}30 -404 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}30

  播放段落

  We can then use another trig relationship to find the length of the hypotenuse:
  ::然后我们可以用另一种三角关系 来寻找低耗的长度:

  播放段落

  $$\begin{array}{rl}\sin {30}^{\circ }& =\frac{opposite}{hypotenuse}=\frac{4.04}{c}\\ \sin {30}^{\circ }& =\frac{4.04}{c}\\ c\sin {30}^{\circ }& =4.04\\ c& =\frac{4.04}{\sin {30}^{\circ }}\approx 8.08\end{array}$$

  
  ::30°C 30°C 30°C 4°Csin 30°Csin 30°Csin 30°C4c 4°C 4°C 30°C 30°C 8.08°C

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked how far the ball is from the pole.
  ::之前有人问你球离杆子有多远

  播放段落

  From our knowledge of how to , we can set up a triangle with the rope and the pole, like this:
  ::根据我们对如何, 我们可以用绳子和杆子 建立一个三角形,像这样:

  

  播放段落

  From this, it is straightforward to set up a trig relationship for sine that can help:
  ::由此可以直截了当地建立三重关系:

  播放段落

  $$\begin{array}{r}\sin {35}^{\circ }=\frac{opposite}{1}\\ (1)\sin {35}^{\circ }=opposite\\ opposite\approx .5736\end{array}$$

  
  ::对面1(1)sin_35_对面poriteporite_5736

  播放段落

  Example 2
  ::例2

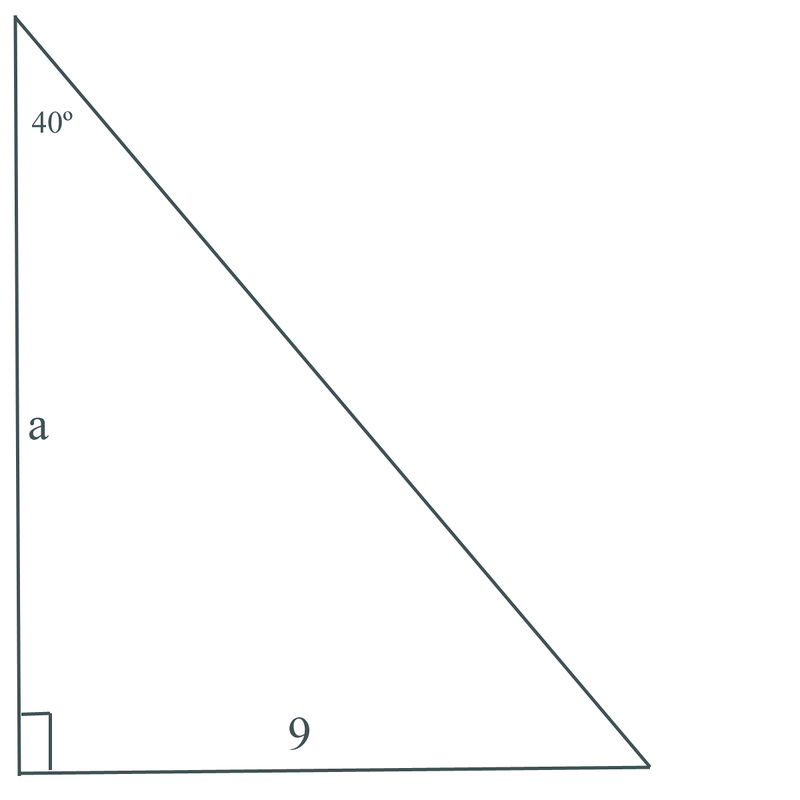
  播放段落

  Solve the triangle shown below:
  ::解析以下三角形 :

  

  播放段落

   Since the angle given is $\begin{array}{r}{40}^{\circ }\end{array}$ , and the length of the side opposite the angle is 9, we can use the tangent function to determine the length of the side adjacent to the angle:
  ::由于给定角度为 40, 而角度对面的长度为 9, 我们可以使用正切函数来决定角旁边的边的长度 :

  播放段落

  $$\begin{array}{r}\tan {40}^{\circ }=\frac{9}{a}\\ a=\frac{9}{\tan {40}^{\circ }}\\ a=\frac{9}{.839}\\ a=10.73\end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}40... 9aaa=9tan... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}a=9.839a=10.73 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

  播放段落

  We can then use another trig function to find the length of the hypotenuse:
  ::然后我们再用另一个三角函数 来找到低耗的长度:

  播放段落

  $$\begin{array}{r}\sin {40}^{\circ }=\frac{9}{c}\\ c=\frac{9}{\sin {40}^{\circ }}\\ c=\frac{9}{.643}\\ c=13.997\end{array}$$

  
  ::=9sin =40 =9.643c=13.997 =13.997

  播放段落

  Finally, the other angle in the triangle can be found either by a trigonometric relationship, or by recognizing that the sum of the internal angles of the triangle have to equal $\begin{array}{r}{180}^{\circ }\end{array}$ :
  ::最后,三角形中的另一个角度可以通过三角关系找到,或者通过承认三角形内部角之和必须等于180:

  $$\begin{array}{r}{90}^{\circ }+{40}^{\circ }+\theta ={180}^{\circ }\\ \theta ={180}^{\circ }-{90}^{\circ }-{40}^{\circ }\\ \theta ={50}^{\circ }\end{array}$$

  播放段落

  Example 3
  ::例3

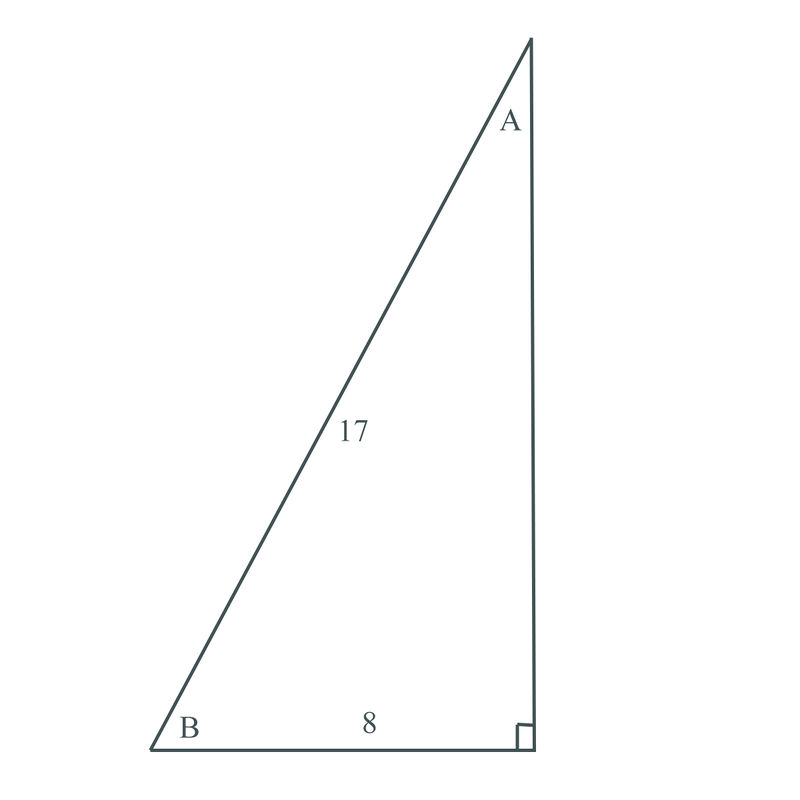
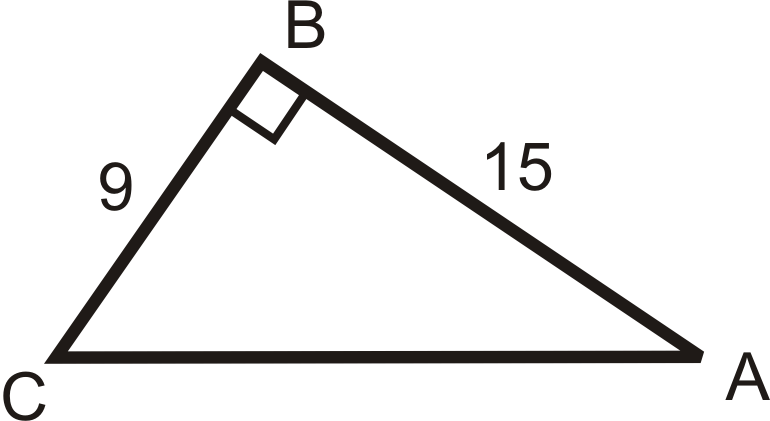
  播放段落

  Solve the triangle shown below:
  ::解析以下三角形 :

  

   

  播放段落

   Since this triangle has two sides given, we can start with the Pythagorean Theorem to find the length of the third side:
  ::因为三角形有两面, 我们可以从毕达哥里安神话开始, 找到第三面的长度:

  播放段落

  $$\begin{array}{r}{a}^2+b^2=c^2\\ 8^2+b^2={17}^2\\ b^2={17}^2-8^2\\ b^2=289-64=225\\ b=15\end{array}$$

  
  ::a2+b2=c282+b2=172b2=172-82b2=289-64=225b=15

  播放段落

  With this knowledge, we can work to find the other two angles:
  ::有了这种知识,我们可以努力找到另外两个角度:

  播放段落

  $$\begin{array}{r}\tan \mathrm{\angle }B=\frac{15}{8}\\ \tan \mathrm{\angle }B=1.875\\ \mathrm{\angle }B={\tan }^{-1}1.875\approx {61.93}^{\circ }\end{array}$$

  
  ::B=158tanB=1.875B=tan-1118.7561.93

  播放段落

  And the final angle is:

  $$\begin{array}{r}{180}^{\circ }-{90}^{\circ }-{61.93}^{\circ }={28.07}^{\circ }\end{array}$$

  
  ::最后一个角度是: 1809061.9328.07

  播放段落

  Example 4
  ::例4

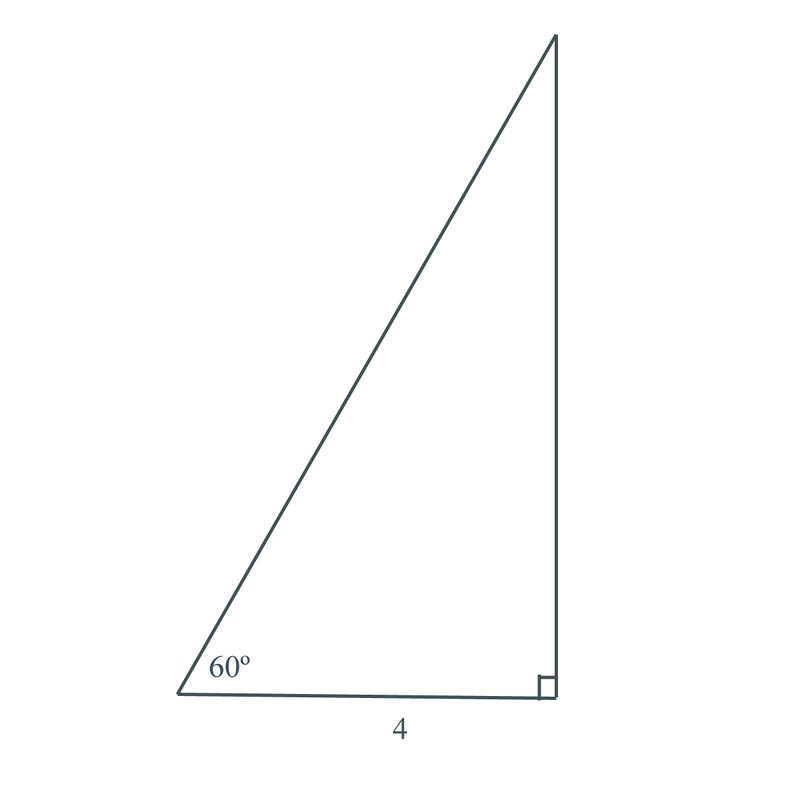
  播放段落

  Solve the triangle shown below:
  ::解析以下三角形 :

  

   

  播放段落

  There are a number of things known about this triangle. Since we know all of the internal angles, there are a few different ways to solve for the unknown sides. Here let's use the $\begin{array}{r}{60}^{\circ }\end{array}$ angle to find the unknown sides:
  ::这个三角形有许多已知的事物。 由于我们了解所有内部角度, 对于未知边有几种不同的解答方法。 这里让我们用 60 角度来找到未知边 :

  播放段落

  $$\begin{array}{r}\tan {60}^{\circ }=\frac{a}{4}\\ a=4\tan {60}^{\circ }\\ a=(4)(1.73)=6.92\end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么?

  播放段落

  and
  ::和

  播放段落

  $$\begin{array}{r}\cos {60}^{\circ }=\frac{4}{h}\\ h=\frac{4}{\cos {60}^{\circ }}\\ h=\frac{4}{.5}\\ h=8\end{array}$$

  
  ::604hh=4cos6045h=8

  播放段落

  So we have found that the lengths of the sides are 4, 8, and 6.92.
  ::因此,我们发现双方的长度是4、8和6.92。

  播放段落

  Review
  ::回顾

  播放段落

  Use the picture below for questions 1-3.
  ::问题1至3请使用下面的图片。

  

  播放段落
  1. Find $\begin{array}{r}m\mathrm{\angle }A\end{array}$ .
     ::找妈妈吧
  播放段落
  2. Find $\begin{array}{r}m\mathrm{\angle }B\end{array}$ .
     ::去找MB
  播放段落
  3. Find the length of AC.
     ::查找 AC 的长度 。

  播放段落

  Use the picture below for questions 4-6.
  ::问题4-6请使用下面的图片。

  

  播放段落
  4. Find $\begin{array}{r}m\mathrm{\angle }A\end{array}$ .
     ::找妈妈吧
  播放段落
  5. Find $\begin{array}{r}m\mathrm{\angle }C\end{array}$ .
     ::寻找 mC。
  播放段落
  6. Find the length of AC.
     ::查找 AC 的长度 。

  播放段落

  Use the picture below for questions 7-9.
  ::问题7-9请使用下面的图片。

  

  播放段落
  7. Find $\begin{array}{r}m\mathrm{\angle }A\end{array}$ .
     ::找妈妈吧
  播放段落
  8. Find $\begin{array}{r}m\mathrm{\angle }B\end{array}$ .
     ::去找MB
  播放段落
  9. Find the length of BC.
     ::查找 BC 的长度 。

  播放段落

  Use the picture below for questions 10-12.
  ::问题10-12请使用下面的图片。

  

  播放段落
  10. Find $\begin{array}{r}m\mathrm{\angle }A\end{array}$ .
      ::找妈妈吧
  播放段落
  11. Find $\begin{array}{r}m\mathrm{\angle }B\end{array}$ .
      ::去找MB
  播放段落
  12. Find the length of AB.
      ::查找AB的长度 。

  播放段落

  Use the picture below for questions 13-15.
  ::问题13-15请使用下面的图片。

  

  播放段落
  13. Find $\begin{array}{r}m\mathrm{\angle }A\end{array}$ .
      ::找妈妈吧
  播放段落
  14. Find $\begin{array}{r}m\mathrm{\angle }C\end{array}$ .
      ::寻找 mC。
  播放段落
  15. Find the length of BC.
      ::查找 BC 的长度 。
  播放段落
  16. Explain when to use a trigonometric ratio to find missing information about a triangle and when to use the Pythagorean Theorem.
      ::解释何时使用三角比来寻找关于三角形的缺失信息,何时使用毕达哥伦理论。
  播放段落
  17. What is the minimum information you need about a triangle in order to solve it?
      ::您需要三角形的最小信息来解答它吗 ?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。