4.8 ASA和AAS三角协调

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section ASA 和 AAS 三角和谐

  Collapse Expand

  ASA 和 AAS 三角和谐

  播放段落

  Angle-Side-Angle Postulate and Angle-Angle-Side Theorem 
  ::角度- 角度- 角度- 角度- 角度- 角度- 角度- 角度- 角度- 角度- 方向理论

  播放段落

  If two angles and one side in one triangle are congruent to the corresponding two angles and one side in another triangle, then the two triangles are congruent. This idea encompasses two triangle congruence shortcuts: Angle-Side-Angle and Angle-Angle-Side.
  ::如果两个角度和一个三角形的一面与相应的两个角度和另一个三角形的一面相匹配,则两个三角形是相同的。这个想法包含两个三角形的一致快捷键:角-Side-Agle和角-Agle-Sgle-Side。

  播放段落

  Angle-Side-Angle (ASA) Congruence Postulate : If two angles and the included side in one triangle are congruent to two angles and the included side in another triangle, then the two triangles are congruent.
  ::角度- 角度- 角度- 角度( ASA) 相容性 假设 : 如果两个角度和一个三角形中包含的侧面与两个角度一致, 而另一个三角形中包含的侧面相同, 那么两个三角形是相容的 。

  播放段落

  Angle-Angle-Side (AAS) Congruence Theorem : If two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle, then the triangles are congruent.
  ::角度- 角度- 侧( AAS) 共性理论 : 如果两个角度和一个三角形中未包含的侧面与两个角度一致, 而另一个三角形中相应的非包含的侧面相同, 那么三角形是相同的 。

  播放段落

  The placement of the word Side is important because it indicates where the side that you are given is in relation to the angles. The pictures below help to show the difference between the two shortcuts.
  ::Side 字的位置很重要, 因为它显示给您提供的侧面与角度的关系。 下面的图片有助于显示两个快捷键之间的差异 。

  播放段落

  ASA
  ::ASA 亚SA

  播放段落

  AAS
  ::AASAAAAAAAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS(AAAS)AAS(AAS(AAAAAS(AAAAAAAAAAAAA

  播放段落

  What if you were given two triangles and provided with only the measure of two of their angles and one of their side lengths? How could you determine if the two triangles were congruent? 
  ::假若你们获得两个三角形,而你们得享受两个三角形和两个三角形及一个三角形的边距,你们怎能断定这两个三角形是否相容呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

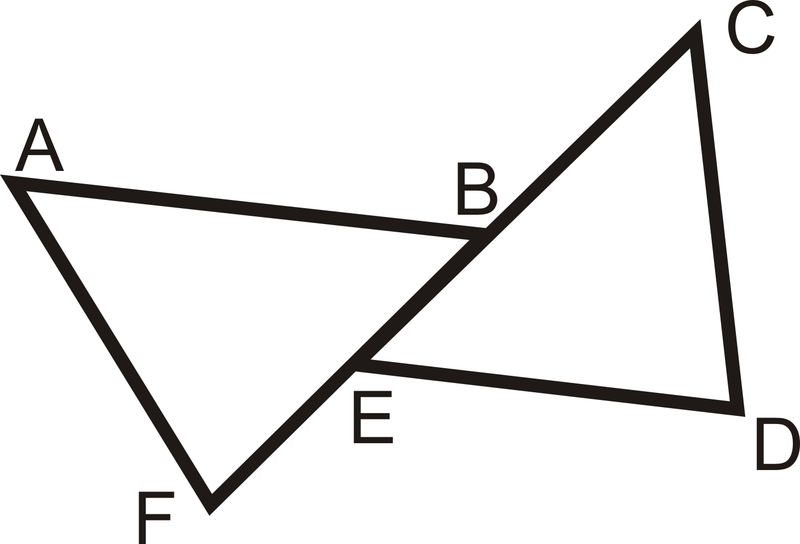
  播放段落

  Can you prove that the following triangles are congruent? Why or why not?
  ::您能否证明以下三角形是相容的? 为何或为何不?

  

  播放段落

  We cannot show the triangles are congruent because $\begin{align*}\overline{KL}\end{align*}$ and $\begin{align*}\overline{ST}\end{align*}$ are not corresponding , even though they are congruent. To determine if $\begin{align*}\overline{KL}\end{align*}$ and $\begin{align*}\overline{ST}\end{align*}$ are corresponding, look at the angles around them, $\begin{align*}\angle K\end{align*}$ and $\begin{align*}\angle L\end{align*}$ and $\begin{align*}\angle S\end{align*}$ and $\begin{align*}\angle T\end{align*}$ . $\begin{align*}\angle K\end{align*}$ has one arc and $\begin{align*}\angle L\end{align*}$ is unmarked. $\begin{align*}\angle S\end{align*}$ has two arcs and $\begin{align*}\angle T\end{align*}$ is unmarked. In order to use AAS, $\begin{align*}\angle S\end{align*}$ needs to be congruent to $\begin{align*}\angle K\end{align*}$ .
  ::我们无法显示三角形是相容的,因为即使三角形是相匹配的, 也与三角形不相匹配。 要确定三角形是否对应, 请看看周围的角, KandLandSandT. @Khasonearc和Lisnotolates。 Shas twoarcs和Tisnotolates。 为了使用 AAS, 需要与K一致 。 @\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Example 2
  ::例2

  播放段落

  Write a 2-column proof.
  ::写两栏证明书

  

  播放段落

  Given : $\begin{align*}\overline{AB} || \overline{ED}, \ \angle C \cong \angle F, \ \overline{AB} \cong \overline{ED}\end{align*}$
  ::有了: 有了,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有,有

  播放段落

  Prove : $\begin{align*}\overline{AF} \cong \overline{CD}\end{align*}$
  ::证明:

  Statement	Reason
  1. $\begin{align*}\overline{AB} || \overline{ED}, \ \angle C \cong \angle F, \ \overline{AB} \cong \overline{ED}\end{align*}$	1. Given
  2. $\begin{align*}\angle ABE \cong \angle DEB\end{align*}$	2. Theorem
  3. $\begin{align*}\triangle ABF \cong \triangle DEC\end{align*}$	3. ASA
  4. $\begin{align*}\overline{AF} \cong \overline{CD}\end{align*}$	4. (Corresponding Parts of are Congruent)

  播放段落

  Example 3
  ::例3

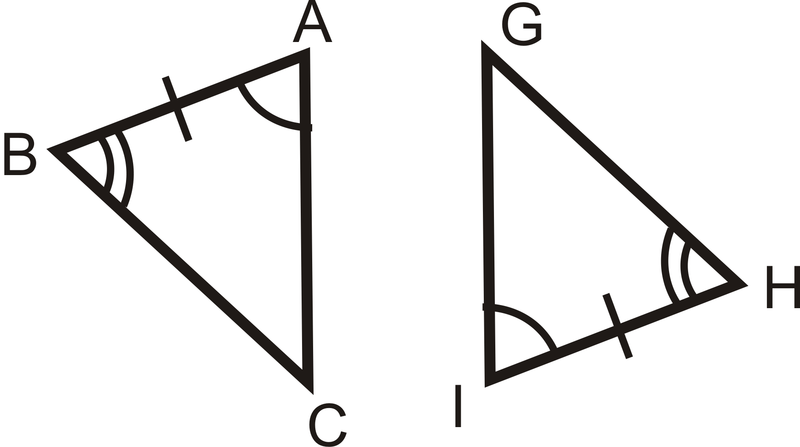
  播放段落

  What information do you need to prove that these two triangles are congruent using the ASA Postulate,  $\begin{align*}\overline{AB} \cong \overline{UT}\end{align*}$ ,  $\begin{align*}\overline{AC} \cong \overline{UV}\end{align*}$ ,  $\begin{align*}\overline{BC} \cong \overline{TV}\end{align*}$ , or  $\begin{align*}\angle B \cong \angle T\end{align*}$ ?
  ::你需要什么信息来证明这两个三角形 使用ASA的假设是吻合的 AC'UV,BC'TV,还是'B'T?

  

  播放段落

  For ASA, we need the side between the two given angles, which is $\begin{align*}\overline{AC}\end{align*}$ and $\begin{align*}\overline{UV}\end{align*}$ . The answer is  $\begin{align*}\overline{AC} \cong \overline{UV}\end{align*}$ . 
  ::对于ASA,我们需要两个角度之间的一面, 即AC和UV。答案是AC'UV。

  播放段落

  Example 4
  ::例4

  播放段落

  Write a 2-column proof.
  ::写两栏证明书

  播放段落

  Given : $\begin{align*}\angle C \cong \angle E, \ \overline{AC} \cong \overline{AE}\end{align*}$
  ::以:C'E,AC'AE

  播放段落

  Prove : $\begin{align*}\triangle ACF \cong \triangle AEB\end{align*}$
  ::证明:@AACF_AEB

  

  Statement	Reason
  1. $\begin{align*}\angle C \cong \angle E, \ \overline{AC} \cong \overline{AE}\end{align*}$	1. Given
  2. $\begin{align*}\angle A \cong \angle A\end{align*}$	2. Reflexive PoC
  3. $\begin{align*}\triangle ACF \cong \triangle AEB\end{align*}$	3. ASA

  播放段落

  Example 5
  ::例5

  播放段落

  What information do you need to prove that these two triangles are congruent using ASA? AAS?
  ::您需要哪些信息来证明这两个三角形 使用 ASA 具有相似性? AAS 吗 ?

  

  播放段落

  For ASA, we need the angles on the other side of $\begin{align*}\overline{EF}\end{align*}$ and $\begin{align*}\overline{QR}\end{align*}$ . $\begin{align*}\angle F \cong \angle Q\end{align*}$
  ::对于ASA,我们需要角度 在EF和R的另一侧。

  播放段落

  For AAS, we would need the other angle. $\begin{align*}\angle G \cong \angle P\end{align*}$
  ::对于AAS,我们需要另一个角度。

  播放段落

  Review
  ::回顾

  播放段落

  For questions 1-3, determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
  ::对于问题1-3,请确定三角形是否一致。如果是,请写一致的语句,以及您使用的一致的假设或定理。

  1. 
  2. 
  3. 

  播放段落

  For questions 4-8, use the picture and the given information below.
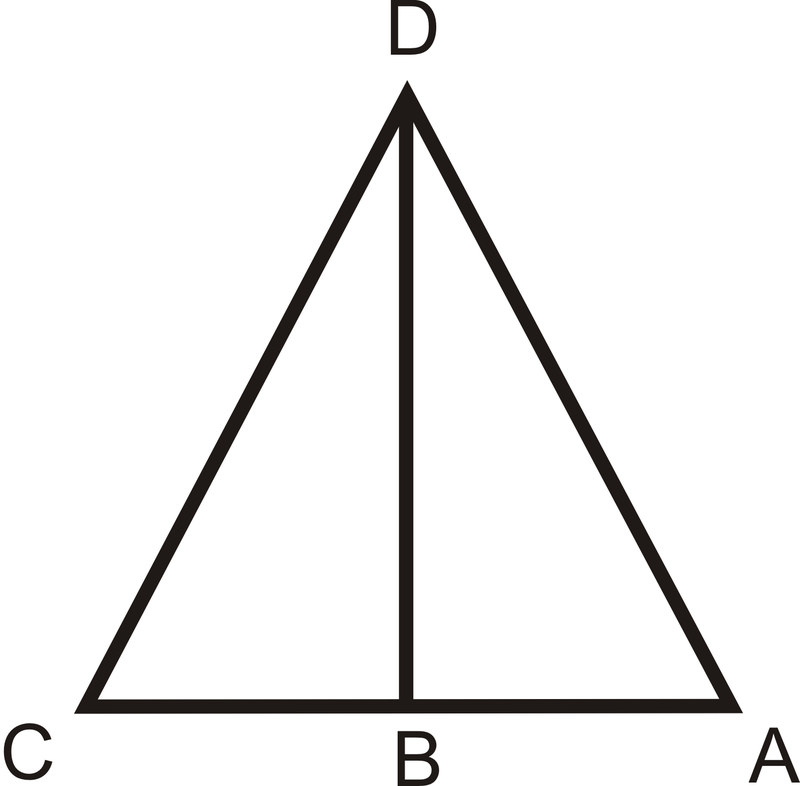
  ::问题4-8,请使用下文的图片和说明。

  

  播放段落

  Given : $\begin{align*}\overline{DB} \perp \overline{AC}, \ \overline{DB}\end{align*}$ is the angle bisector of $\begin{align*}\angle CDA\end{align*}$
  ::依据:DB=AC,DB是 CDA的角角

  播放段落
  4. From $\begin{align*}\overline{DB} \perp \overline{AC}\end{align*}$ , which angles are congruent and why?
     ::DB'AC,哪个角度是一致的,为什么?
  播放段落
  5. Because $\begin{align*}\overline{DB}\end{align*}$ is the angle bisector of $\begin{align*}\angle CDA\end{align*}$ , what two angles are congruent?
     ::因为DB是QCDA的双角部分, 有两个角度是相同的?
  播放段落
  6. From looking at the picture, what additional piece of information are you given? Is this enough to prove the two triangles are congruent?
     ::从图片来看,你还提供了哪些补充信息?这足以证明这两个三角是相容的吗?
  播放段落
  7. Write a 2-column proof to prove $\begin{align*}\triangle CDB \cong \triangle ADB\end{align*}$ , using #4-6.
     ::使用#4-6来写一个2栏的证明 来证明卡布卡巴德银行。
  播放段落
  8. What would be your reason for $\begin{align*}\angle C \cong \angle A\end{align*}$ ?
     ::你会有什么理由 给"CA"?

  播放段落

  For questions 9-13, use the picture and the given information.
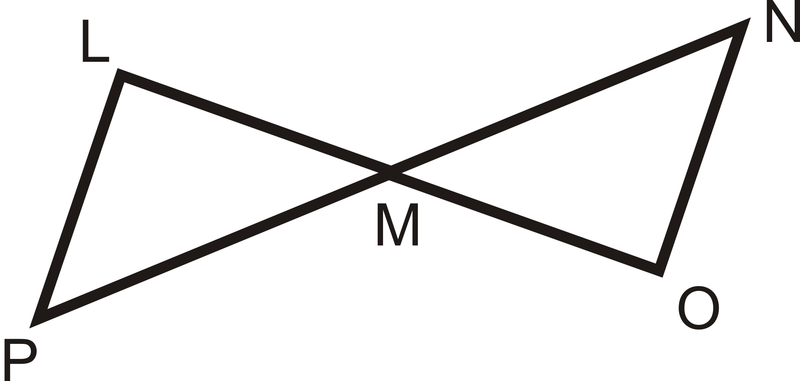
  ::对于问题9-13,请使用图片和提供的信息。

  播放段落

  Given : $\begin{align*}\overline{LP}||\overline{NO}, \ \overline{LP} \cong \overline{NO}\end{align*}$
  ::面对:不,不,不

  

  播放段落
  9. From $\begin{align*}\overline{LP}||\overline{NO}\end{align*}$ , which angles are congruent and why?
     ::从LP不,哪个角度是一致的,为什么?
  播放段落
  10. From looking at the picture, what additional piece of information can you conclude?
      ::从情况来看,你还能得出什么结论?
  播放段落
  11. Write a 2-column proof to prove $\begin{align*}\triangle LMP \cong \triangle OMN\end{align*}$ .
      ::写一个2栏证明 证明LMPOMN。
  播放段落
  12. What would be your reason for $\begin{align*}\overline{LM} \cong \overline{MO}\end{align*}$ ?
      ::你为何要这么做?
  播放段落
  13. Fill in the blanks for the proof below. Use the given from above. Prove : $\begin{align*}M\end{align*}$ is the midpoint of $\begin{align*}\overline{PN}\end{align*}$ .
      ::填满空白以证明下面的证据。 请使用上面给出的。 证明: M 是中点 。

  Statement	Reason
  1. $\begin{align*}\overline{LP} || \overline{NO}, \ \overline{LP} \cong \overline{NO}\end{align*}$	1. Given
  2.	2. Alternate Interior Angles
  3.	3. ASA
  4. $\begin{align*}\overline{LM} \cong \overline{MO}\end{align*}$	4.
  5. $\begin{align*}M\end{align*}$ is the midpoint of $\begin{align*}\overline{PN}\end{align*}$ .	5.

  播放段落

  Determine the additional piece of information needed to show the two triangles are congruent by the given postulate.
  ::确定显示两个三角形所需的额外信息与给定的假设一致。

  播放段落
  14. AAS
      ::AASAAAAAAAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS(AAAS)AAS(AAS(AAAAAS(AAAAAAAAAAAAA
  播放段落
  15. ASA
      ::ASA 亚SA
  播放段落
  16. ASA
      ::ASA 亚SA
  播放段落
  17. AAS
      ::AASAAAAAAAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS)AAS(AAS(AAS)AAS(AAS(AAAS)AAS(AAS(AAAAAS(AAAAAAAAAAAAA

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

   

  播放段落

  Resources
  ::资源