1.12 三角区域替代公式

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节三角区域替代公式

  折叠 展开

  三角区域替代公式

  You are studying the Gulf of Mexico in your Geography class. Your Instructor brings up the idea of the Bermuda Triangle. This is a place where, according to some, many planes get lost. Here is an illustration of it:

  播放段落

  The first thing this makes you think of is your math class, since that class is your favorite. You would like to know just how big the Bermuda Triangle is. Unfortunately, the Bermuda Triangle isn't a right triangle. However, you do know that the lengths of one of the sides is 950 miles, the other side is 975 miles, and the angle between them is $\begin{array}{r}{60}^{\circ }\end{array}$ .
  ::这让你想到的第一件事就是你的数学课, 因为那课是你最喜欢的。 您想知道百慕大三角有多大。 不幸的是, 百慕大三角不是一个正确的三角。 但是, 您知道, 一边的长度是950英里, 另一边是975英里, 而它们之间的角是60英里。

  播放段落

  Is there any way to use this information to help you find out just how big the Bermuda Triangle is?
  ::有没有办法利用这些信息 来帮助你发现百慕大三角有多大?

  播放段落

  Area of a Triangle
  ::三角三角区域区域

  播放段落

  In Geometry, you learned that the area of a triangle is $\begin{array}{r}A=\frac{1}{2}bh\end{array}$ , where $\begin{array}{r}b\end{array}$ is the base and $\begin{array}{r}h\end{array}$ is the height, or altitude.
  ::在几何学中,你了解到三角形的区域是A=12bh, b是基数, h是高度, 或高度。

  播放段落

  Now that you know the trig ratios, this formula can be changed around, using sine.
  ::既然你知道三角比, 这个公式可以改变, 使用正弦 。

  

  播放段落

  Looking at the triangle above, you can use sine to determine $\begin{array}{r}h,\sin C=\frac{h}{a}\end{array}$ . So, solving this equation for $\begin{array}{r}h\end{array}$ , we have $\begin{array}{r}a\sin C=h\end{array}$ . Substituting this for $\begin{array}{r}h\end{array}$ , we now have a new formula for area.
  ::查看上面的三角形, 您可以使用正弦来确定 h, sinC=ha。 因此, 解开这个公式, 我们有 asinC=h。 将这个公式替换为 h, 我们现在有一个新的区域公式 。

  播放段落

  $$\begin{array}{r}A=\frac{1}{2}ab\sin C\end{array}$$

  
  ::A=12absinC

  播放段落

  What this means is you do not need the height to find the area anymore. All you now need is two sides and the angle between the two sides, called the included angle.
  ::这意味着您不再需要高度来找到区域。 您现在需要的只是两面和两面之间的角, 称为包含角度 。

  播放段落

  Finding Area
  ::寻找地区

  1. 

  

  播放段落

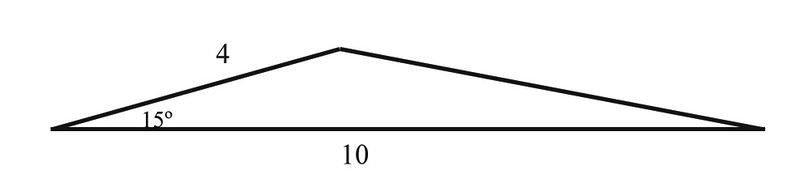
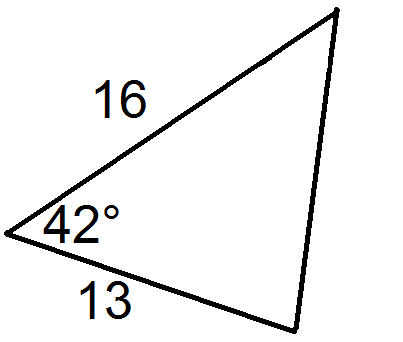
  Using the formula, $\begin{array}{r}A=\frac{1}{2}ab\sin C\end{array}$ , we have
  ::使用公式A=12 absinC

  播放段落

  $$\begin{array}{rl}A& =\frac{1}{2}\cdot 8\cdot 13\cdot \sin {82}^{\circ }\\ & =4\cdot 13\cdot 0.990\\ & =51.494\end{array}$$

  
  ::A=1281338844130.990=51.494

  2. 

  

  播放段落

  Recall that a parallelogram can be split into two triangles. So the formula for a parallelogram, using the new formula, would be: $\begin{array}{r}A=2\cdot \frac{1}{2}ab\sin C\end{array}$ or $\begin{array}{r}A=ab\sin C\end{array}$ .
  ::回顾平行图可以分为两个三角形。 因此使用新公式的平行图公式将是: A=212 absinC 或 A=absinC 。

  播放段落

  $$\begin{array}{rl}A& =7\cdot 15\cdot \sin {65}^{\circ }\\ & =95.162\end{array}$$

  
  ::A=7=15sin6595.162

  3. 

  

  播放段落

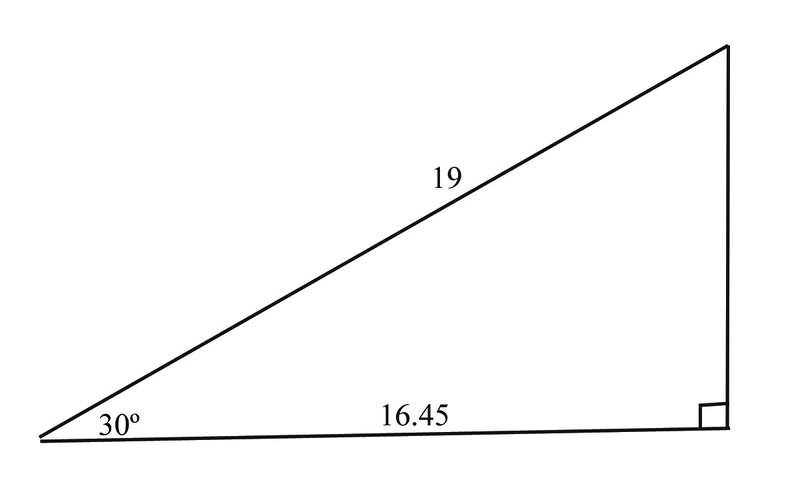
   Using the formula, $\begin{array}{r}A=\frac{1}{2}ab\sin C\end{array}$ , we have
  ::使用公式A=12 absinC

  播放段落

  $$\begin{array}{rl}A& =\frac{1}{2}\cdot 16.45\cdot 19\cdot \sin {30}^{\circ }\\ & =8.225\cdot 19\cdot 0.5\\ & =78.14\end{array}$$

  
  ::A=1216.4519308.225190.5=78.14。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked how big the Bermuda Triangle is.
  ::之前有人问你百慕大三角有多大

  播放段落

  Now that you know the equation for the area of a triangle in terms of two of the sides and the included angle, we can use that to solve for the area of the Bermuda Triangle:
  ::既然你们知道三角形的方程式, 以两边和包括的角度来表示, 我们可以用这个方程式来解决百慕大三角区:

  播放段落

  $$\begin{array}{r}A=\frac{1}{2}ab\sin \theta \\ A=\frac{1}{2}(950)(975)\sin {60}^{\circ }\\ A=\frac{1}{2}(950)(975)(.866)\\ A=401066.25\end{array}$$

  
  ::A=12absinA=12(950)(975sin60)A=12(950)(975)(866)A=401066.25

  播放段落

  The area of the triangle is approximately 401,006 square miles.
  ::三角形面积约为401,006平方英里。

  播放段落

  Example 2
  ::例2

  播放段落

   Find the area of the triangle.
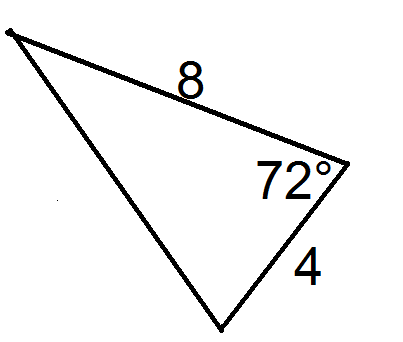
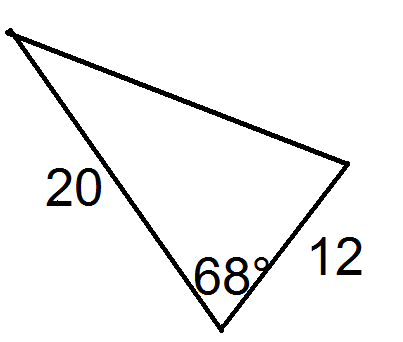
  ::找到三角形的区域 。

  

  播放段落

  Using the formula, $\begin{array}{r}A=\frac{1}{2}ab\sin C\end{array}$ , we have
  ::使用公式A=12 absinC

  播放段落

  $$\begin{array}{rl}A& =\frac{1}{2}\cdot 4\cdot 10\cdot \sin {15}^{\circ }\\ & =2\cdot 10\cdot 0.2589\\ & =5.178\end{array}$$

  
  ::A=124106152100.2589=5.178

  播放段落

  Example 3
  ::例3

  播放段落

  Find the area of the triangle.
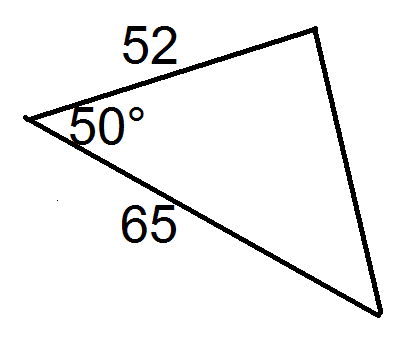
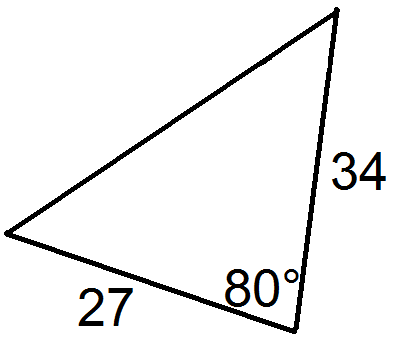
  ::找到三角形的区域 。

  

  播放段落

  Using the formula, $\begin{array}{r}A=\frac{1}{2}ab\sin C\end{array}$ , we have
  ::使用公式A=12 absinC

  播放段落

  $$\begin{array}{rl}A& =\frac{1}{2}\cdot 8\cdot 15\cdot \sin {25}^{\circ }\\ & =4\cdot 15\cdot 0.4226\\ & =25.356\end{array}$$

  
  ::A=1281515254150.4226=25.356

  播放段落

  Example 4
  ::例4

  播放段落

  Find the area of the triangle.
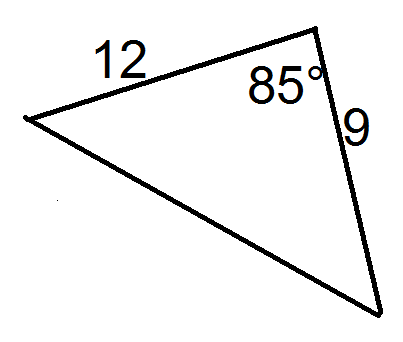
  ::找到三角形的区域 。

  

   

  播放段落

  Using the formula, $\begin{array}{r}A=\frac{1}{2}ab\sin C\end{array}$ , we have
  ::使用公式A=12 absinC

  播放段落

  $$\begin{array}{rl}A& =\frac{1}{2}\cdot 10\cdot 11\cdot \sin {32}^{\circ }\\ & =5\cdot 11\cdot 0.53\\ & =29.15\end{array}$$

  
  ::A=1210111135110.53=29.15

  播放段落

  Review
  ::回顾

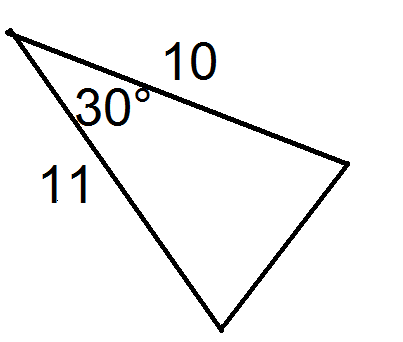
  播放段落

  Use the following picture for questions 1 and 2.
  ::问题1和2使用以下图片。

  

  播放段落
  1. If b is the shorter side length, find the values of a, b, and C needed for the formula to find the area of the triangle.
     ::如果 b 是 较短的侧边长度, 则找到公式需要的 a、 b 和 C 值, 以找到三角形的区域 。
  播放段落
  2. Now find the area of the triangle.
     ::现在找到三角形的区域 。

  播放段落

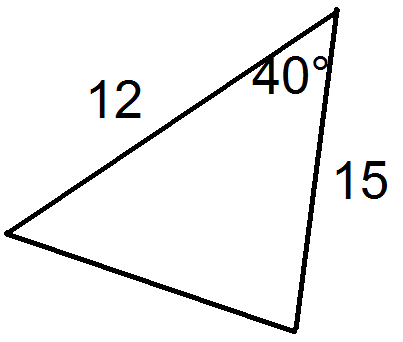
  Use the following picture for questions 3 and 4.
  ::问题3和4使用以下图片。

  

  播放段落
  3. If b is the shorter side length, find the values of a, b, and C needed for the formula to find the area of the triangle.
     ::如果 b 是 较短的侧边长度, 则找到公式需要的 a、 b 和 C 值, 以找到三角形的区域 。
  播放段落
  4. Now find the area of the triangle.
     ::现在找到三角形的区域 。

  播放段落

  Find the area of each triangle below.
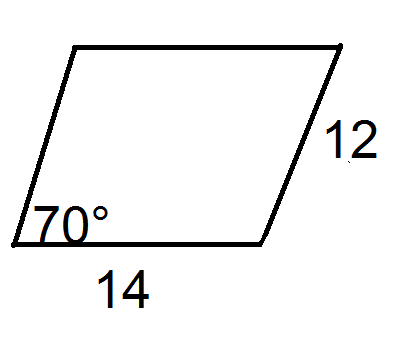
  ::查找下方每个三角形的区域 。

  5. 

  6. 

  7. 

  8. 

  9. 

  10. 

  11. 

  播放段落

  Find the area of each parallelogram.
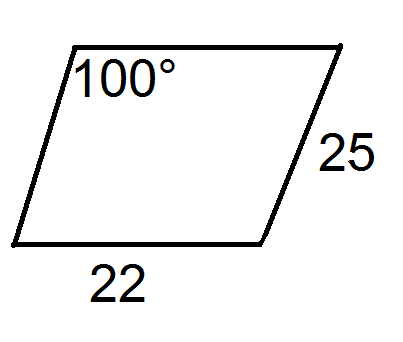
  ::查找每个平行图的区域 。

  12. 

  13. 

  播放段落
  14. Describe another way you could have found the area of the parallelogram in the previous problem.
      ::描述上一个问题中您可能找到平行图的区域的另一种方式 。
  播放段落
  15. When you first learned about sine, you learned how it worked for right triangles. Explain why this method for calculating area uses sine, but works for non-right triangles.
      ::当您第一次了解正弦时, 您就会了解它是如何为右三角形工作的。 解释为什么此计算区域的方法使用正弦, 但用于非右三角形 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。