Course: 4.10 伊索塞尔三角

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

同位素三角

Isosceles Triangles
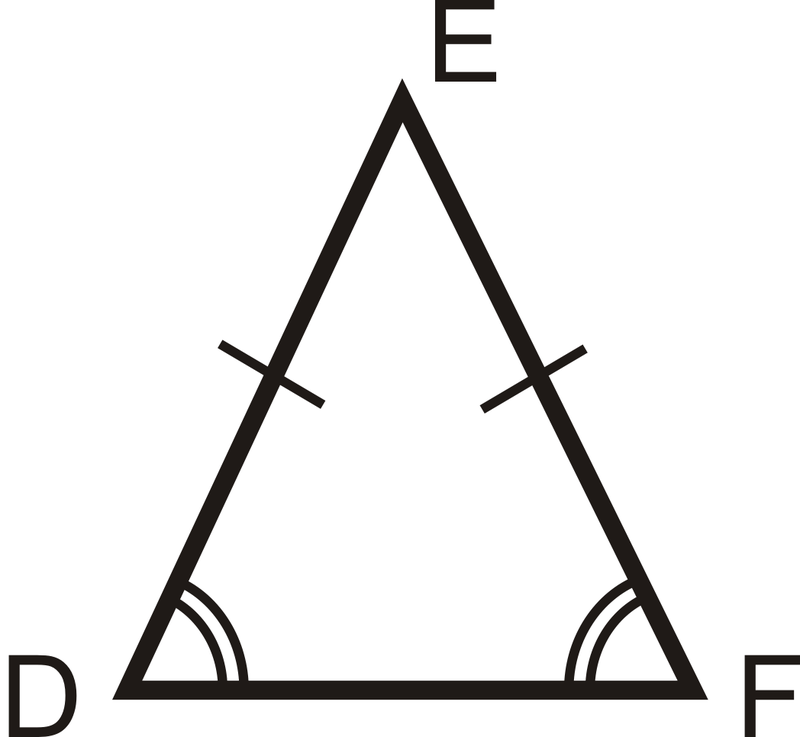
::同位素三角

An isosceles triangle is a triangle that has at least two congruent sides. The congruent sides of the isosceles triangle are called the legs . The other side is called the base . The angles between the base and the legs are called base angles . The angle made by the two legs is called the vertex angle . One of the important properties of isosceles triangles is that their base angles are always congruent. This is called the Base Angles Theorem .
::等星三角形是一个三角形,至少有两个相容的两边。等星三角形的相容两边被称为腿。另一边称为底部。基底和腿之间的角称为基底角。两腿之间的角称为顶端角。等星三角形的一个重要特性是其基底角总是相容的。这称为底底角角理论。

For $\begin{align*}\triangle DEF\end{align*}$ , if $\begin{align*}\overline{DE} \cong \overline{EF}\end{align*}$ , then $\begin{align*}\angle D \cong \angle F\end{align*}$ .
::对于国防,如果 ef'f,那么d'f。

Another important property of isosceles triangles is that the angle bisector of the vertex angle is also the perpendicular bisector of the base. This is called the Isosceles Triangle Theorem . ( Note this is ONLY true of the vertex angle. ) The converses of the Base Angles Theorem and the Isosceles Triangle Theorem are both true as well.
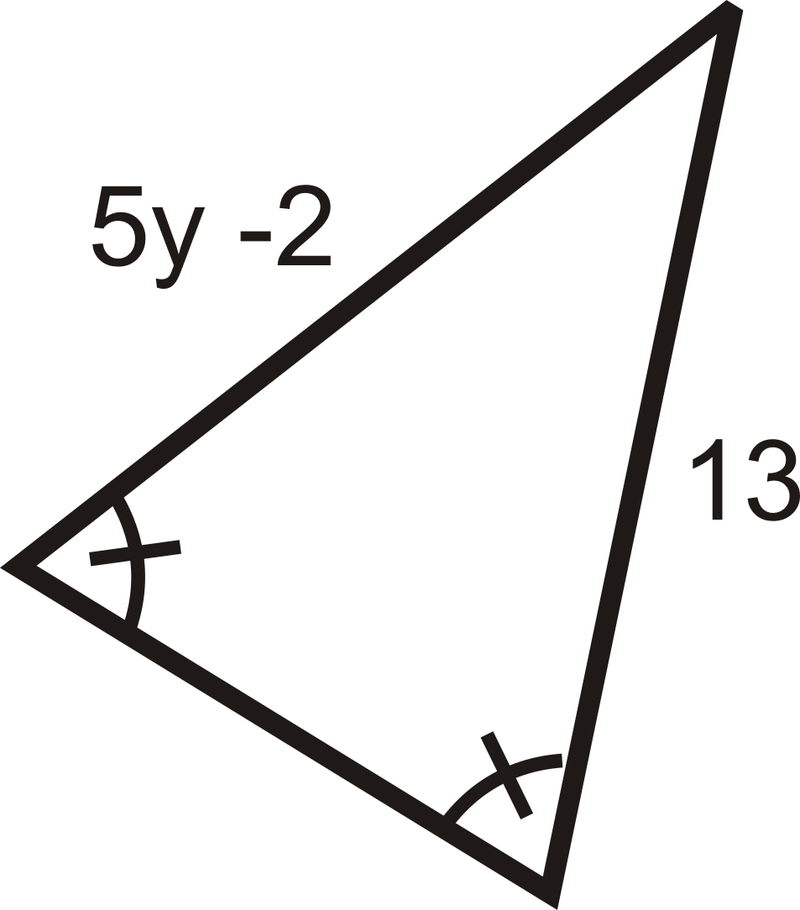
::Isosceles三角形的另一个重要属性是,顶端角角的角两部分也是基底的直角两部分。这称为Isosceles三角定理。 (请注意,顶端角度只有这样。 ) 底部角定理和底部角三角定理的反义都是真实的。

Base Angles Theorem Converse : If two angles in a triangle are congruent, then the sides opposite those angles are also congruent. So for $\begin{align*}\triangle DEF\end{align*}$ , if $\begin{align*}\angle D \cong \angle F\end{align*}$ , then $\begin{align*}\overline{DE} \cong \overline{EF}\end{align*}$ .
::底角理论对立: 如果三角形中的两个角度是相同的, 那么这些角度对面的两边也是相同的。所以对于“ DEF ” 来说, 如果是“ DF ” , 那么是“ DE ” 。

Isosceles Triangle Theorem Converse: The perpendicular bisector of the base of an isosceles triangle is also the angle bisector of the vertex angle. So for isosceles $\begin{align*}\triangle DEF\end{align*}$ , if $\begin{align*}\overline{EG} \perp \overline{DF}\end{align*}$ and $\begin{align*}\overline{DG} \cong \overline{GF}\end{align*}$ , then $\begin{align*}\angle DEG \cong \angle FEG\end{align*}$ .
::Isosceles三角理论对立:一个等骨质三角基底的直角两侧部分也是顶端角的角两侧部分。对于Iosceles QDEF,如果是 EG 和 DG 和 DG ,那么是 DEG 和 DEG 和 DEG 和 DEG 和 DEG 和 DEG 和 DEG 。

What if you were presented with an isosceles triangle and told that its base angles measure $\begin{align*}x^\circ\end{align*}$ and $\begin{align*}y^\circ\end{align*}$ ? What could you conclude about x and y ?
::如果有人向你们介绍一个等离子三角形,并告诉你们其基角是测量 x 和 y 的尺度呢? 关于 x 和 y,你能得出什么结论?

Examples
::实例

Example 1
::例1

Find the value of $\begin{align*}x\end{align*}$ and the measure of each angle.
::查找 x 值和每个角度的度量。

The two angles are equal, so set them equal to each other and solve for $\begin{align*}x\end{align*}$ .
::这两个角度是相等的, 所以把它们等同起来, 解决 x 。

\begin{aligned} (4 x + 12)^{\circ} & = (5 x - 3)^{\circ} \\ 15 = x \end{aligned}

$\begin{align*}(4x+12)^\circ & = (5x-3)^\circ\\ 15 = x\end{align*}$
:

4x+12) (5x-3) 15=x

Substitute $\begin{align*}x = 15\end{align*}$ ; the base angles are $\begin{align*}[4(15) +12]^\circ\end{align*}$ , or $\begin{align*}72^\circ\end{align*}$ . The vertex angle is $\begin{align*}180^\circ -72^\circ-72^\circ =36^\circ\end{align*}$ .
::替代 x=15; 底角为 [( 15) +12] 或 72 。顶点角为 180 72 72 36 。

Example 2
::例2

True or false: Base angles of an isosceles triangle can be right angles.
::真实的或假的: 等离子三角形的基础角度可以是右角度。

This statement is false. Because the base angles of an isosceles triangle are congruent, if one base angle is a right angle then both base angles must be right angles. It is impossible to have a triangle with two right ( $\begin{align*}90^\circ\end{align*}$ ) angles. The Triangle Sum Theorem states that the sum of the three angles in a triangle is $\begin{align*}180^\circ\end{align*}$ . If two of the angles in a triangle are right angles, then the third angle must be $\begin{align*}0^\circ\end{align*}$ and the shape is no longer a triangle.
::此语句是虚假的。因为等分三角形的基角度是相容的, 如果一个基角度是右角, 那么两个基角度必须是右角。三角形 Sumorem 表示三角形中三个角度的总和是 180 。如果三角形中两个角度是右角, 那么第三个角度必须是 0 , 形状不再是三角形。

Example 3
::例3

Which two angles are congruent?
::哪个角度与哪个角度一致?

This is an isosceles triangle. The congruent angles are opposite the congruent sides. From the arrows we see that $\begin{align*}\angle S \cong \angle U\end{align*}$ .
::这是一个等星三角形。相近角度对着相近边。从箭头中可以看到 {S_U } 。

Example 4
::例4

If an isosceles triangle has base angles with measures of $\begin{align*}47^\circ\end{align*}$ , what is the measure of the vertex angle?
::如果一等分三角形的基角为47,则顶端角的量度为多少?

Draw a picture and set up an equation to solve for the vertex angle, $\begin{align*}v\end{align*}$ . Remember that the three angles in a triangle always add up to $\begin{align*}180^\circ\end{align*}$ .
::绘制图片并设置一个方程来解决顶点角度, v. 记住三角形中的三个角度总相加到 180 。

\begin{aligned} 47^{\circ} + 47^{\circ} + v & = 180^{\circ} \\ v & = 180^{\circ} - 47^{\circ} - 47^{\circ} \\ v & = 86^{\circ} \end{aligned}

$\begin{align*}47^\circ + 47^\circ + v & = 180^\circ\\ v & = 180^\circ - 47^\circ - 47^\circ\\ v & = 86^\circ\end{align*}$
::4747*v=180*v=180*_47*_47*v=86*}

Example 5
::例5

If an isosceles triangle has a vertex angle with a measure of $\begin{align*}116^\circ\end{align*}$ , what is the measure of each base angle?
::如果一等分形三角形有一个顶端角, 度量为 116 , 那么每个基角的度量是多少 ?

Draw a picture and set up and equation to solve for the base angles, $\begin{align*}b\end{align*}$ .
::为基准角度绘制图片、设置方程式和方程式,b。

\begin{aligned} 116^{\circ} + b + b & = 180^{\circ} \\ 2 b & = 64^{\circ} \\ b & = 32^{\circ} \end{aligned}

$\begin{align*}116^\circ + b + b & = 180^\circ\\ 2b & = 64^\circ\\ b & = 32^\circ\end{align*}$
::116b+b=1802b=64b=32

Review
::回顾

Find the measures of $\begin{align*}x\end{align*}$ and/or $\begin{align*}y\end{align*}$ .
::查找 x 和/或 Y 的量度。

Determine if the following statements are true or false.
::确定以下声明是真实的还是虚假的。

Base angles of an isosceles triangle are congruent.
::等分形三角形的基角度是相容的。

Base angles of an isosceles triangle are complementary.
::等分三角形的底角是互补的。

Base angles of an isosceles triangle can be equal to the vertex angle.
::等分三角形的基角度可以等于顶点角度。

Base angles of an isosceles triangle are acute.
::等分形三角形的底角是急性的。

Fill in the proofs below.
::填写以下证据。

Given : Isosceles $\begin{align*}\triangle CIS\end{align*}$ , with base angles $\begin{align*}\angle C\end{align*}$ and $\begin{align*}\angle S\end{align*}$ $\begin{align*}\overline{IO}\end{align*}$ is the angle bisector of $\begin{align*}\angle CIS\end{align*}$ Prove : $\begin{align*}\overline{IO}\end{align*}$ is the perpendicular bisector of $\begin{align*}\overline{CS}\end{align*}$
::参考:IO是CS的直角两侧部分。

*Statement*	*Reason*
1.	1. Given
2.	2. Base Angles Theorem
3. $\begin{align}\angle CIO \cong \angle SIO\end{align}$	3.
4.	4. Reflexive PoC
5. $\begin{align}\triangle CIO \cong \triangle SIO\end{align}$	5.
6. $\begin{align}\overline{CO} \cong \overline{OS}\end{align}$	6.
7.	7. CPCTC
8. $\begin{align}\angle IOC\end{align}$ and $\begin{align}\angle IOS\end{align}$ are supplementary	8.
9.	9. Congruent Supplements Theorem
10. $\begin{align}\overline{IO}\end{align}$ is the perpendicular bisector of $\begin{align}\overline{CS}\end{align}$	10.

Given : Isosceles $\begin{align*}\triangle ICS\end{align*}$ with $\begin{align*}\angle C\end{align*}$ and $\begin{align*}\angle S\end{align*}$ $\begin{align*}\overline{IO}\end{align*}$ is the perpendicular bisector of $\begin{align*}\overline{CS}\end{align*}$ Prove : $\begin{align*}\overline{IO}\end{align*}$ is the angle bisector of $\begin{align*}\angle CIS\end{align*}$
::说明:IO是CIS的侧角,

*Statement*	*Reason*
1.	1.
2. $\begin{align}\angle C \cong \angle S\end{align}$	2.
3. $\begin{align}\overline{CO} \cong \overline{OS}\end{align}$	3.
4. $\begin{align}m\angle IOC = m\angle IOS = 90^\circ\end{align}$	4.
5.	5.
6.	6. CPCTC
7. $\begin{align}\overline{IO}\end{align}$ is the angle bisector of $\begin{align}\angle CIS\end{align}$	7.

On the $\begin{align*}x-y\end{align*}$ plane, plot the coordinates and determine if the given three points make a scalene or isosceles triangle.
::在 x - y 平面上,绘制坐标并确定给定的三点是否形成比例尺或等分三角形。

(-2, 1), (1, -2), (-5, -2)
(-2, 5), (2, 4), (0, -1)
(6, 9), (12, 3), (3, -6)
(-10, -5), (-8, 5), (2, 3)
(-1, 2), (7, 2), (3, 9)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

同位素三角

Isosceles Triangles ::同位素三角

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源