1.14 右三角、环形和其他应用

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 右三角、环形和其他应用

  Collapse Expand

  右三角、环形和其他应用

  While on a camping trip with your friends, you take an orienteering trip. You end up on a course which results in you hiking $\begin{array}{r}{30}^{\circ }\end{array}$  west of due s outh . This is represented as $\begin{array}{r}S{30}^{\circ }W\end{array}$  (always start with N  or  S, then the number of degrees to the east or west of there). You hike until you are 5 miles from where you started. Is it possible to determine how far  w est you are from where you started?

  播放段落

  Bearings
  ::环环

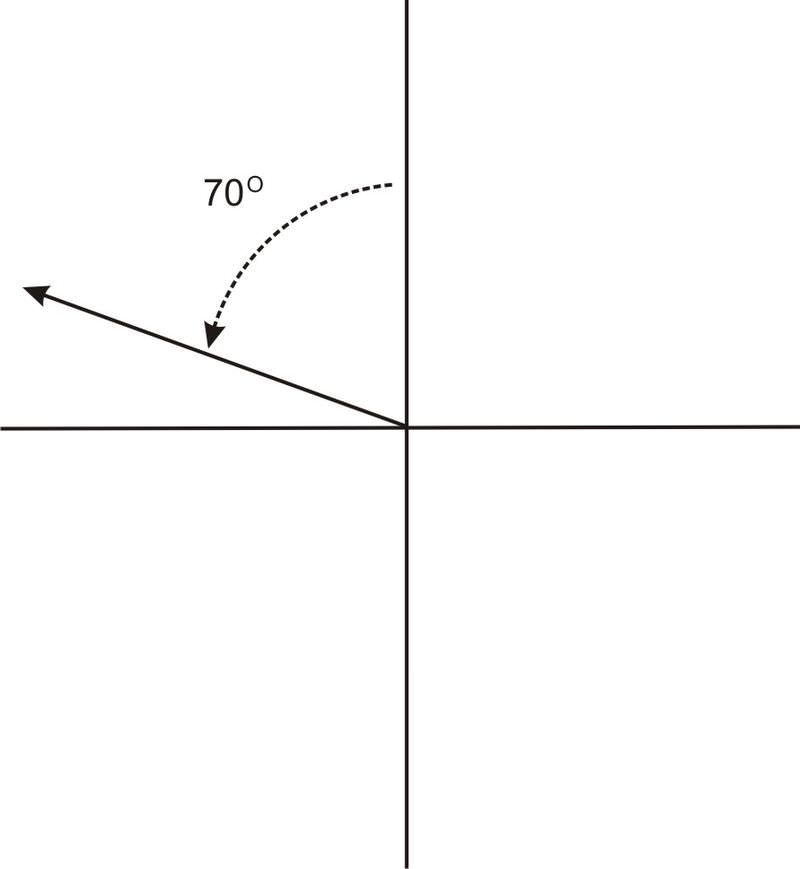
  播放段落

  You can  use right triangles to find distances using angles given as bearings . In navigation, a bearing is the direction from one object to another. In air navigation, bearings are given as angles rotated clockwise from the north.
  ::您可以使用右三角来使用给定的轴轴作为轴承来寻找距离。在导航中,轴承是从一个对象到另一个对象的方向。在空中导航中,轴承是按时钟从北方旋转的角度。

  播放段落

  The graph below shows an angle of 70 degrees:
  ::下图显示70度角:

  

  播放段落

  It is important to keep in mind that angles in navigation problems are measured this way, and not the same way angles are otherwise measured in trigonometry. Further, angles in navigation and surveying may also be given in terms of north, east, south, and west. For example, $\begin{array}{r}N{70}^{\circ }E\end{array}$ refers to an angle  70 degrees to the east of straight  north, while $\begin{array}{r}N{70}^{\circ }W\end{array}$ refers to an angle  70 degrees west of straight north. $\begin{array}{r}N{70}^{\circ }E\end{array}$ is the same as the angle shown in the graph above. $\begin{array}{r}N{70}^{\circ }W\end{array}$ would result in an angle in the second quadrant, like this:
  ::必须铭记,航行问题的角度以这种方式测量,而不是以同样的方式在三角测量中测量角度。此外,航行和勘测的角度也可以以北、东、南和西为单位。例如,N70-E指直北以东70度的角,N70-W指直向北以西70度的角。N70-E与上图所示的角相同。N70-W将导致第二个方位的角,如:

  

  播放段落

  Now, let's look at a problem where we find the distance using right triangles as bearings.
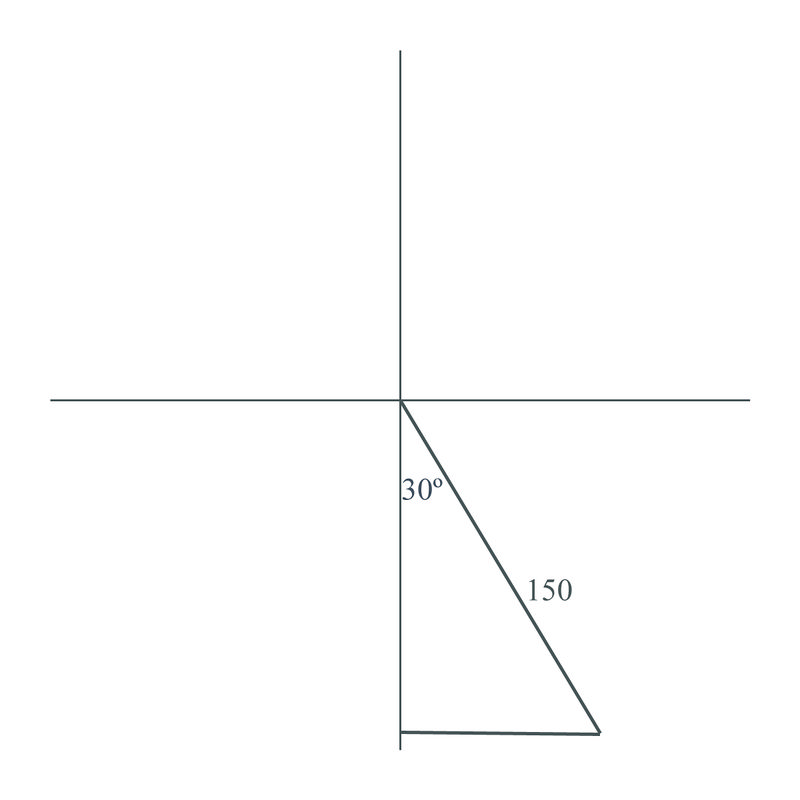
  ::现在,让我们来研究一个问题, 我们用右三角形作为轴承找到距离。

  播放段落

  A ship travels on a $\begin{array}{r}N{50}^{\circ }E\end{array}$ course. The ship travels until it is due north of a port which is 10 nautical miles due east of the port from which the ship originated. How far did the ship travel?
  ::船舶在AN50-Ecourse上行驶,一直行驶到离船舶发端港东面10海里处的港口北端。

  

  播放段落

  The angle between $\begin{array}{r}d\end{array}$ and 10 nm is the complement of $\begin{array}{r}{50}^{\circ }\end{array}$ , which is $\begin{array}{r}{40}^{\circ }\end{array}$ . Therefore we can find $\begin{array}{r}d\end{array}$ using the cosine function:
  ::d 和 10 nm 之间的角是 50 + 的补充, 也就是 40 + 。 因此, 我们可以使用 cosine 函数找到 d :

  播放段落

  $$\begin{array}{rl}\cos {40}^{\circ }& =\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{10}{d}\\ \cos {40}^{\circ }& =\frac{10}{d}\\ d\cos {40}^{\circ }& =10\\ d& =\frac{10}{\cos {40}^{\circ }}\approx 13.05\text{nautical miles}\end{array}$$

  
  ::10ddcos 40 10dcos 40 10d= 10cos 40\ 13.05海里

  播放段落

  An airplane flies on a course of $\begin{array}{r}S{30}^{\circ }E\end{array}$ , for 150 km. How far south is the plane from where it originated?
  ::飞机在S30-E航道上飞行150公里。 飞机从何方起飞,南边有多远?

  播放段落

  C onstruct a triangle using the known information, and then use the cosine function to solve the problem:
  ::使用已知信息构造三角形, 然后使用余弦函数解决问题 :

  

  播放段落

  $$\begin{array}{rl}\cos {30}^{\circ }& =\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{y}{150}\\ \cos {30}^{\circ }& =\frac{y}{150}\\ 150\cos {30}^{\circ }& =y\\ y& =150\cos {30}^{\circ }\approx 130\text{ km}\end{array}$$

  
  ::约150科 30 y150150150科 30 y yy =150科 30 yy = 150科 30 130公里

  播放段落

  Jean travels to school each day by walking 200 meters due n orth, and then turning right and walking 100 meters due eEast. If she had walked in a straight line, what would the angle between her home and the school be if the beginning of the angle is taken from due n orth ? What would be two different ways to describe the direction to take walking there in a straight line, using what we've learned in this section?
  ::Jean每天步行200米往北走,然后向右走,然后向东走100米。如果她走直线,那么如果从正北走开,她家和学校之间的角度会是什么?用我们在这段学到的东西来描述走直线的方向,有什么两种不同的方式?

  播放段落

  From the triangle given above, we can use the tangent function to determine the angle if she had walked in a straight line.
  ::从上面给定的三角形中,我们可以使用正切函数来确定如果她走过一条直线的角。

  播放段落

  $$\begin{array}{rl}\tan \theta & =\frac{\text{opposite}}{\text{adjacent}}=\frac{100}{200}\\ \tan \theta & =\frac{100}{200}\\ \theta & ={26.57}^{\circ }\end{array}$$

  
  ::

  播放段落

  One way of describing her straight line path is how far e ast of north she is: $\begin{array}{r}N{26.57}^{\circ }E\end{array}$
  ::N26.57-E

  播放段落

  Also, since we know the bearings are usually based off of n orth, her motion can be described as simply a bearing of  $\begin{array}{r}{26.57}^{\circ }.\end{array}$
  ::而且,因为我们知道轴线通常位于北面之外, 她的动议可以说只是26.57。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given some information about a hiking trip, and asked "I s it possible to determine how far s outh you are from where you started?"
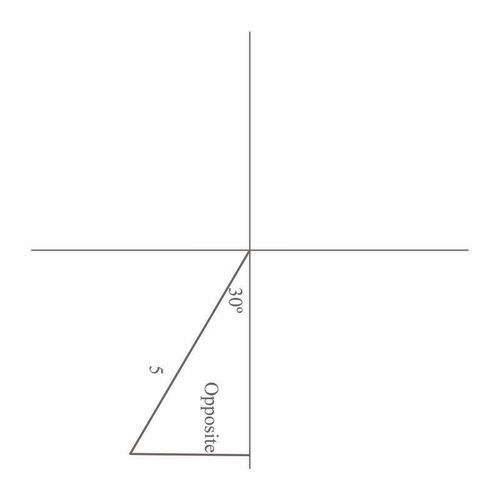
  ::早些时候,有人给了你一些有关远足旅行的信息, 并问道,“你能否确定你离起步地的南边有多远?”

  播放段落

  The story specified that you hiked for 5 miles from your starting point, on a bearing of $\begin{array}{r}S{30}^{\circ }W.\end{array}$  Applying this data with your  understanding of how to construct a triangle using bearings, you can draw the following:
  ::该故事具体说明了您在 S30 W 的轴承上从起点爬了5英里。 在应用这些数据时, 了解如何使用轴承构建三角形时, 您可以绘制以下信息 :

  

  
  

  播放段落

  This shows that the opposite side of the triangle is what's not known. Therefore, you can use the sine function to solve the problem:
  ::这显示三角形的对面是未知的。 因此, 您可以使用正弦函数来解决问题 :

  播放段落

  $$\begin{array}{r}\sin {30}^{\circ }=\frac{\text{opposite}}{5}\\ \text{opposite}=5\sin {30}^{\circ }\\ \text{opposite}=(5)(.5)=2.5\end{array}$$

  
  ::对面5对面5对面5对面=5对面30对对面(5)对面(5)对面=2.5

  播放段落

  You are 2.5 miles w est of where you started.
  ::你距起步地西边2.5英里

  播放段落

  Example 2
  ::例2

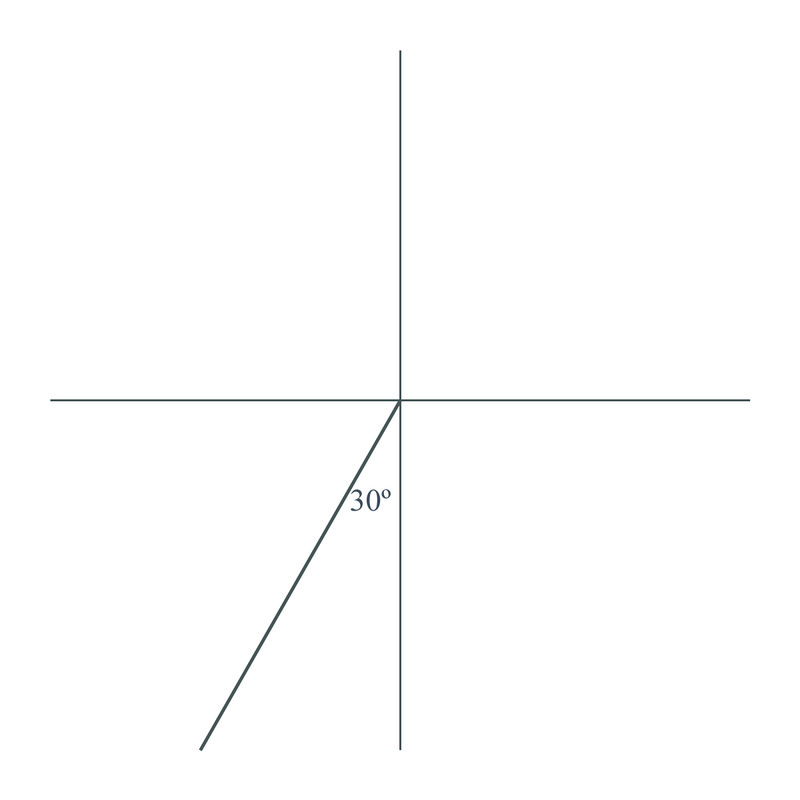
  播放段落

  Plot a course or bearing of  $\begin{array}{r}{240}^{\circ }\end{array}$  on a rectangular coordinate system.
  ::在矩形坐标系统上绘制课程或带240。

  播放段落

  T his is the same as  $\begin{array}{r}S{30}^{\circ }W\end{array}$  (recall that due south is 270 degrees, so 240 degrees is 30 degrees wast of that) and can be plotted as :
  ::这与S30W(提醒注意向南为270摄氏度,因此240摄氏度为30摄氏度)相同,可绘制为:

   

  播放段落

  Example 3
  ::例3

  播放段落

  Scott is boating on a course of $\begin{array}{r}N{15}^{\circ }E\end{array}$ . What course would he need to take to return to where he came from?
  ::Scott正在N15E航道上划船

  播放段落

  The opposite direction would return him to his starting point. This would be $\begin{array}{r}S{15}^{\circ }W\end{array}$ .
  ::反方向会让他回到起点 这是S15W

  播放段落

  Example 4
  ::例4

  播放段落

  Adam hikes on a course of $\begin{array}{r}N{47}^{\circ }E\end{array}$ for 7 km. How far e ast is Adam from where he started?  
  ::亚当在N47E的航道上足足7公里。

   

  播放段落

  Fi nd the length of the triangle above (which is how far Adam traveled e ast) by using the sine function:
  ::通过使用正弦函数查找上面三角形的长度(即亚当向东走多远) :

  播放段落

  $$\begin{array}{r}\sin {47}^{\circ }=\frac{x}{7}\\ x=7\sin {47}^{\circ }\\ x=(7)(.7313)\\ x=5.1191\end{array}$$

  
  ::=7sin=47*x7x=(7)(7313x=5.1191)

  播放段落

  He is 5.1191 km east of where he started.
  ::他位于他起步地以东5.1191公里处。

  播放段落

  Review
  ::回顾

  播放段落
  1. Plot a course of $\begin{array}{r}N{40}^{\circ }E\end{array}$ on a rectangular coordinate system.
     ::在矩形坐标系统上绘制N40E线。
  播放段落
  2. Plot a course of $\begin{array}{r}N{60}^{\circ }E\end{array}$ on a rectangular coordinate system.
     ::绘制N60-Eon的航道,一个矩形坐标系统。
  播放段落
  3. Plot a course of $\begin{array}{r}S{70}^{\circ }W\end{array}$ on a rectangular coordinate system.
     ::在矩形坐标系统上绘制S70W的路线。
  播放段落
  4. Plot a course of $\begin{array}{r}S{5}^{\circ }W\end{array}$ on a rectangular coordinate system.
     ::在矩形坐标系统上绘制 S5W 的路线 。
  播放段落
  5. Plot a course of $\begin{array}{r}N{42}^{\circ }W\end{array}$ on a rectangular coordinate system.
     ::在矩形坐标系统上绘制N42W的航道。
  播放段落
  6. You are on a course of $\begin{array}{r}N{55}^{\circ }E\end{array}$ . What course would you need to take to return to where you came from?
     ::你在N55E轨道上,你需要走哪条路线才能回到你出生的地方?
  播放段落
  7. You are on a course of $\begin{array}{r}S{34}^{\circ }W\end{array}$ . What course would you need to take to return to where you came from?
     ::你在S34QW中,你需要走哪条路才能回到你来的地方?
  播放段落
  8. You are on a course of $\begin{array}{r}N{72}^{\circ }W\end{array}$ . What course would you need to take to return to where you came from?
     ::你在N72W的航道上。 你需要走哪条航道才能回到你来的地方?
  播放段落
  9. You are on a course of $\begin{array}{r}S{10}^{\circ }E\end{array}$ . What course would you need to take to return to where you came from?
     ::你在S10E中,你需要上哪门课才能回到你来的地方?
  播放段落
  10. You are on a course of $\begin{array}{r}N{25}^{\circ }W\end{array}$ . What course would you need to take to return to where you came from?
      ::你在N25W的航道上。 你需要走哪条航道才能回到你来的地方?
  播放段落
  11. You are on a course of $\begin{array}{r}N{47}^{\circ }E\end{array}$ for 5 km. How far e ast are you from where you started?
      ::你在N47E航道上5公里 距离你起步的东边有多远?
  播放段落
  12. You are on a course of $\begin{array}{r}S{32}^{\circ }E\end{array}$ for 8 km. How far e ast are you from where you started?
      ::你在S32E的航道上8公里。你离起步地有多远?
  播放段落
  13. You are on a course of $\begin{array}{r}N{15}^{\circ }W\end{array}$ for 10 km. How far w est are you from where you started?
      ::你在N15W航道上10公里 你从哪儿开始的西边有多远?
  播放段落
  14. You are on a course of $\begin{array}{r}S{3}^{\circ }W\end{array}$ for 12 km. How far w est are you from where you started?
      ::你在S3W航程上12公里 距离起步地的西边有多远?
  播放段落
  15. You are on a course of $\begin{array}{r}S{67}^{\circ }E\end{array}$ for 6 km. How far e ast are you from where you started?
      ::6公里长的S67E航程 离起点还有多远?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。