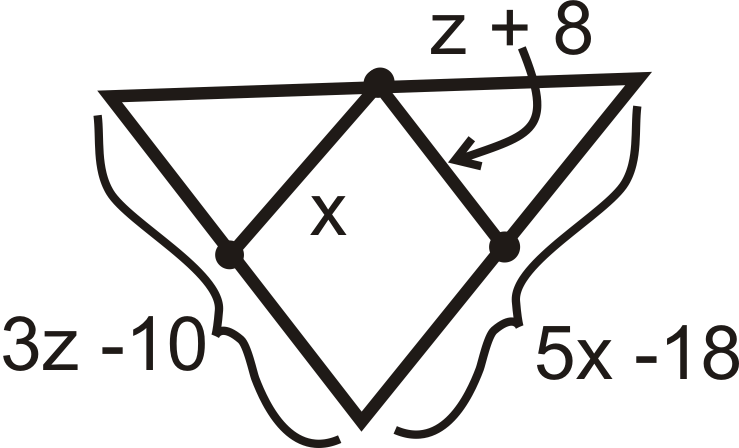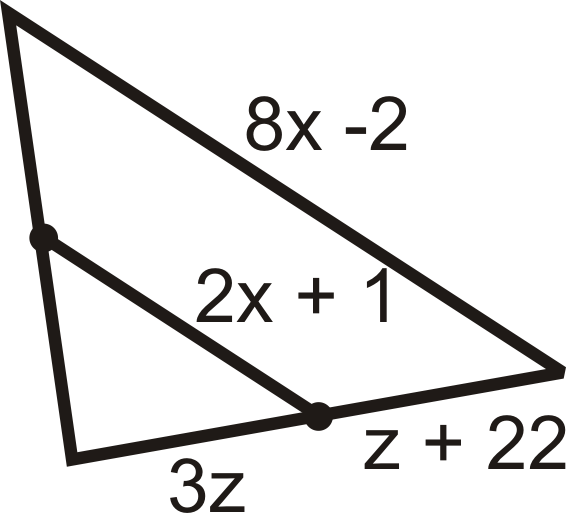课程： 5.1 中段定理 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节中段定理

折叠展开
中段定理
Midsegment Theorem
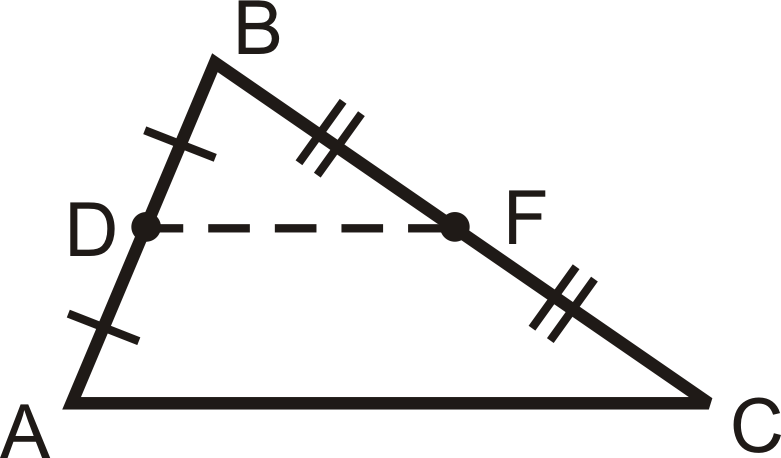
::中段定理

A line segment that connects two midpoints of the sides of a triangle is called a midsegment . $\begin{aligned} \bar{D F} \end{aligned}$ is the midsegment between $\begin{aligned} \bar{A B} \end{aligned}$ and $\begin{aligned} \bar{B C} \end{aligned}$ .
::连接三角形两边两中点的线段称为中点。 DF 是AB 和 BC 之间的中点。

The tic marks show that $\begin{aligned} D \end{aligned}$ and $\begin{aligned} F \end{aligned}$ are midpoints. $\begin{aligned} \bar{A D} ≅ \bar{D B} \end{aligned}$ and $\begin{aligned} \bar{B F} ≅ \bar{F C} \end{aligned}$ . For every triangle there are three midsegments.
::数字标记显示D和F是中点。 AD DB 和 BF F FC 。每个三角形都有三个中间部分。

There are two important properties of midsegments that combine to make the Midsegment Theorem . The Midsegment Theorem states that the midsegment connecting the midpoints of two sides of a triangle is parallel to the third side of the triangle, and the length of this midsegment is half the length of the third side. So, if $\begin{aligned} \bar{D F} \end{aligned}$ is a midsegment of $\begin{aligned} △ A B C \end{aligned}$ , then $\begin{aligned} D F = \frac{1}{2} A C = A E = E C \end{aligned}$ and $\begin{aligned} \bar{D F} ‖ \bar{A C} \end{aligned}$ .
::中间部分有两个重要属性, 组成中段理论。中段理论指出, 连接三角形两侧中点的中间部分与三角形第三侧平行, 这个中间部分的长度是第三侧长度的一半。因此, 如果 DF 是 QABC 的中间部分, 那么 DF= 12AC= AE= EC 和 DF = AC 的中间部分。

Note that there are two important ideas here. One is that the midsegment is parallel to a side of the triangle. The other is that the midsegment is always half the length of this side.
::请注意这里有两个重要的想法。一个是中间部分与三角形的一边平行。另一个是中间部分总是长度为这一边的一半。

What if you were given $\begin{aligned} △ F G H \end{aligned}$ and told that $\begin{aligned} \bar{J K} \end{aligned}$ was its midsegment? How could you find the length of $\begin{aligned} J K \end{aligned}$ given the length of the triangle's third side, $\begin{aligned} F H \end{aligned}$ ?
::如果你们被告知JK是它的中间部分呢?鉴于三角形第三边的长度,你怎么能找到JK的长度?FH?

Examples
::实例

Example 1
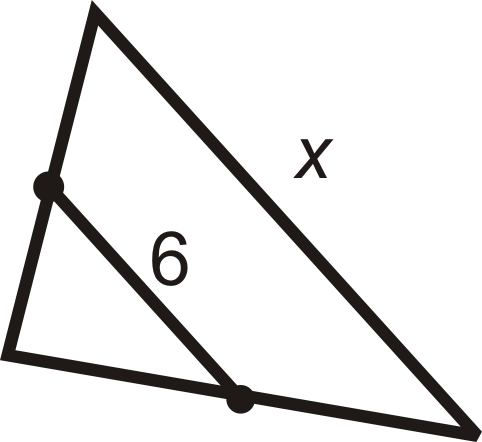
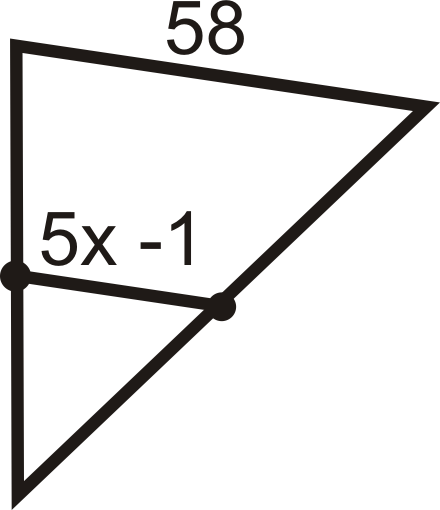
::例1

Find the value of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} A B \end{aligned}$ . $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ are midpoints.
::查找 x 和 AB. A 和 B 的值为中点。

$\begin{aligned} A B = 34 \div 2 = 17 \end{aligned}$ . To find $\begin{aligned} x \end{aligned}$ , set $\begin{aligned} 3 x - 1 \end{aligned}$ equal to 17.
::AB=342=17。要找到 x,设置 3x-1 等于 17。

$\begin{aligned} 3 x - 1 & = 17 \\ 3 x & = 18 \\ x & = 6 \end{aligned}$

::3x-1=173x=18x=6

Example 2
::例2

True or false: If a line passes through two sides of a triangle and is parallel to the third side, then it is a midsegment.
::真实的或假的:如果一条线穿过三角形的两面,与第三面平行,那么它就是一个中间部分。

This statement is false. A line that passes through two sides of a triangle is only a midsegment if it passes through the midpoints of the two sides of the triangle.
::此声明是虚假的。穿过三角形两侧的一条线, 如果穿过三角形两侧的中点, 则只是中间部分。

Example 3
::例3

The vertices of $\begin{aligned} △ L M N \end{aligned}$ are $\begin{aligned} L (4, 5), M (- 2, - 7) \end{aligned}$ and $\begin{aligned} N (- 8, 3) \end{aligned}$ . Find the midpoints of all three sides, label them $\begin{aligned} O, P \end{aligned}$ and $\begin{aligned} Q . \end{aligned}$ Then, graph the triangle, plot the midpoints and draw the midsegments.
::ZLMN的顶点是L(4)、5、M(2-2、-7)和N(-8)、3 找出所有三边的中点,标出O、P和Q。然后,绘制三角形图,绘制中点和中点。

To solve this problem, use the midpoint formula 3 times to find all the midpoints. Recall that the midpoint formula is $\begin{aligned} (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2}) \end{aligned}$ .
::要解决这个问题, 请使用中点公式 3 次来查找所有中点。回顾中点公式是 (x1+x22,y1+y22) 。

$\begin{aligned} L \end{aligned}$ and $\begin{aligned} M = (\frac{4 + (- 2)}{2}, \frac{5 + (- 7)}{2}) = (1, - 1) \end{aligned}$ point $\begin{aligned} O \end{aligned}$
::L和M=(4+(-2)2,5+(-7)2)=(1,-1)O点

$\begin{aligned} M \end{aligned}$ and $\begin{aligned} N = (\frac{- 2 + (- 8)}{2}, \frac{- 7 + 3}{2}) = (- 5, - 2) \end{aligned}$ , point $\begin{aligned} P \end{aligned}$
::M和N=(-2+(-8)2,-7+32)=(-5,-2),P点

$\begin{aligned} L \end{aligned}$ and $\begin{aligned} N = (\frac{4 + (- 8)}{2}, \frac{5 + 3}{2}) = (- 2, 4) \end{aligned}$ , point $\begin{aligned} Q \end{aligned}$
::L和N=(4+(-8)2,5+32)=(-2,4),Q点

Example 4
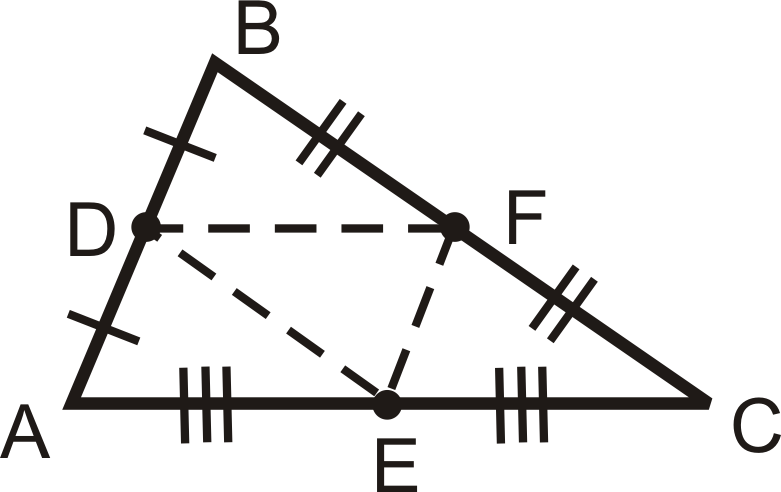
::例4

Mark all the congruent segments on $\begin{aligned} △ A B C \end{aligned}$ with midpoints $\begin{aligned} D, E \end{aligned}$ , and $\begin{aligned} F \end{aligned}$ .
::以中点 D、 E 和 F 标记 ABC 上的所有相容区段。

Drawing in all three midsegments, we have:
::在所有三个中间部分中绘图,我们有:

Also, this means the four smaller triangles are congruent by .
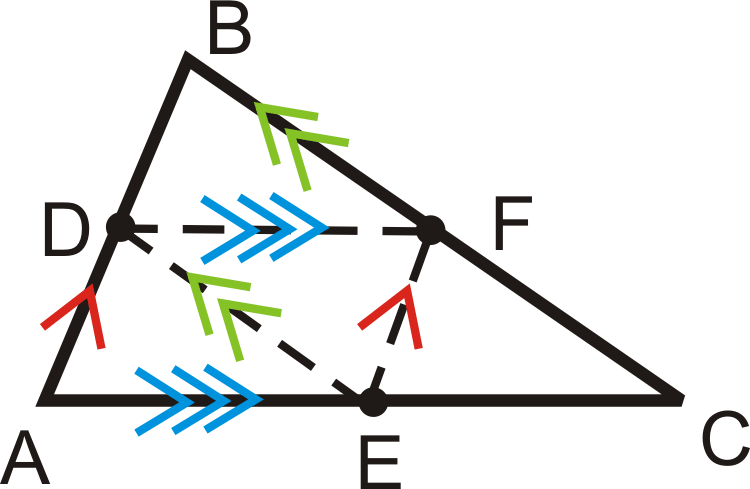
::也意味着四个小三角形是相同的。

Now, mark all the parallel lines on $\begin{aligned} △ A B C \end{aligned}$ , with midpoints $\begin{aligned} D, E \end{aligned}$ , and $\begin{aligned} F \end{aligned}$ .
::现在,用中点D、E和F标记所有在 ABC 上的平行线。

Example 5
::例5

$\begin{aligned} M, N \end{aligned}$ , and $\begin{aligned} O \end{aligned}$ are the midpoints of the sides of $\begin{aligned} △ X Y Z \end{aligned}$ .
::M、N和O是XYZ两侧的中点。

Find $\begin{aligned} M N \end{aligned}$ , $\begin{aligned} X Y \end{aligned}$ , and the perimeter of $\begin{aligned} △ X Y Z \end{aligned}$ .
::找到MN XY和ZXYZ的周边

Use the Midsegment Theorem:
::使用中段定理 :

$\begin{aligned} M N = O Z = 5 \end{aligned}$
::MN=O%5

$\begin{aligned} X Y = 2 (O N) = 2 \cdot 4 = 8 \end{aligned}$
::XY=2(ON)=24=8

Add up the three sides of $\begin{aligned} △ X Y Z \end{aligned}$ to find the perimeter.
::把ZXYZ的三边加起来找到周边

$\begin{aligned} X Y + Y Z + X Z = 2 \cdot 4 + 2 \cdot 3 + 2 \cdot 5 = 8 + 6 + 10 = 24 \end{aligned}$

::XY+YX24+23+25=8+6+10=24

Remember: No line segment over $\begin{aligned} M N \end{aligned}$ means length or distance .
::记住: MN 上无线段表示长度或距离。

Review
::回顾

Determine whether each statement is true or false.
::确定每一声明是真实的还是虚假的。

The endpoints of a midsegment are midpoints.
::中间部分的终点是中点。

A midsegment is parallel to the side of the triangle that it does not intersect.
::中间部分与三角形的侧面平行,而三角形的侧面没有交叉。

There are three similar triangles formed by the midsegments and sides of a triangle.
::三角形的中间部分和侧面形成三个相似的三角形。

There are three possible midsegments in every triangle.
::每个三角形中可能有三个中间部分

$\begin{aligned} R, S, T \end{aligned}$ , and $\begin{aligned} U \end{aligned}$ are midpoints of the sides of $\begin{aligned} △ X P O \end{aligned}$ and $\begin{aligned} △ Y P O \end{aligned}$ .
::R、S、T和U是XPO和YPO两边的中点。

If $\begin{aligned} O P = 12 \end{aligned}$ , find $\begin{aligned} R S \end{aligned}$ and $\begin{aligned} T U \end{aligned}$ .
::如果OP=12,请找到RS和TU。

If $\begin{aligned} R S = 8 \end{aligned}$ , find $\begin{aligned} T U \end{aligned}$ .
::如果RS=8,找到TU

If $\begin{aligned} R S = 2 x \end{aligned}$ , and $\begin{aligned} O P = 20 \end{aligned}$ , find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} T U \end{aligned}$ .
::如果RS=2x和OP=20,则查找x和TU。

If $\begin{aligned} O P = 4 x \end{aligned}$ and $\begin{aligned} R S = 6 x - 8 \end{aligned}$ , find $\begin{aligned} x \end{aligned}$ .
::如果OP=4x和RS=6x-8, 找到x。

For questions 9-15, find the indicated variable(s). You may assume that all line segments within a triangle are midsegments.
::对于问题9-15, 找到指定的变量。您可以假设三角形中的所有线段都是中间部分。

The sides of $\begin{aligned} △ X Y Z \end{aligned}$ are 26, 38, and 42. $\begin{aligned} △ A B C \end{aligned}$ is formed by joining the midpoints of $\begin{aligned} △ X Y Z \end{aligned}$ .

What are the lengths of the sides of $\begin{aligned} △ A B C \end{aligned}$ ?
::ABC两边的长度是多少?

Find the perimeter of $\begin{aligned} △ A B C \end{aligned}$ .
::找到ABC的周边

Find the perimeter of $\begin{aligned} △ X Y Z \end{aligned}$ .
::找到ZXYZ的周界

What is the relationship between the perimeter of a triangle and the perimeter of the triangle formed by connecting its midpoints?
::三角形的周边与三角形通过连接中点而形成的周边之间有什么关系?

::XYZ的两边是26、38和42。ZXYZ的两边是加入ZXYZ的中点形成的。 QABC的两边长度是多少? 找到QABC的周界。找到ZXYZ的周界。三角形的周界与通过连接其中点而形成的三角形的周界之间有什么关系?

Coordinate Geometry Given the vertices of $\begin{aligned} △ A B C \end{aligned}$ below find the midpoints of each side.
::坐标几何根据以下QABC的顶点找到每侧的中点

$\begin{aligned} A (5, - 2), B (9, 4) \end{aligned}$ and $\begin{aligned} C (- 3, 8) \end{aligned}$
::A(5,-2)、B(9,4)和C(3,3,8)

$\begin{aligned} A (- 10, 1), B (4, 11) \end{aligned}$ and $\begin{aligned} C (0, - 7) \end{aligned}$
::A(-10,1,1,B(4,11)和C(0,-7)

$\begin{aligned} A (- 1, 3), B (5, 7) \end{aligned}$ and $\begin{aligned} C (9, - 5) \end{aligned}$
::A(-1,3)、B(5,7)和C(9,5)

$\begin{aligned} A (- 4, - 15), B (2, - 1) \end{aligned}$ and $\begin{aligned} C (- 20, 11) \end{aligned}$
::A(-4,-15)、B(-2,-1)和C(-20,11)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

常规

中段定理

Midsegment Theorem ::中段定理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Midsegment Theorem
::中段定理

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源