Course: 5.2 垂直两侧部门

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

垂直两侧部门

Perpendicular Bisector Theorem
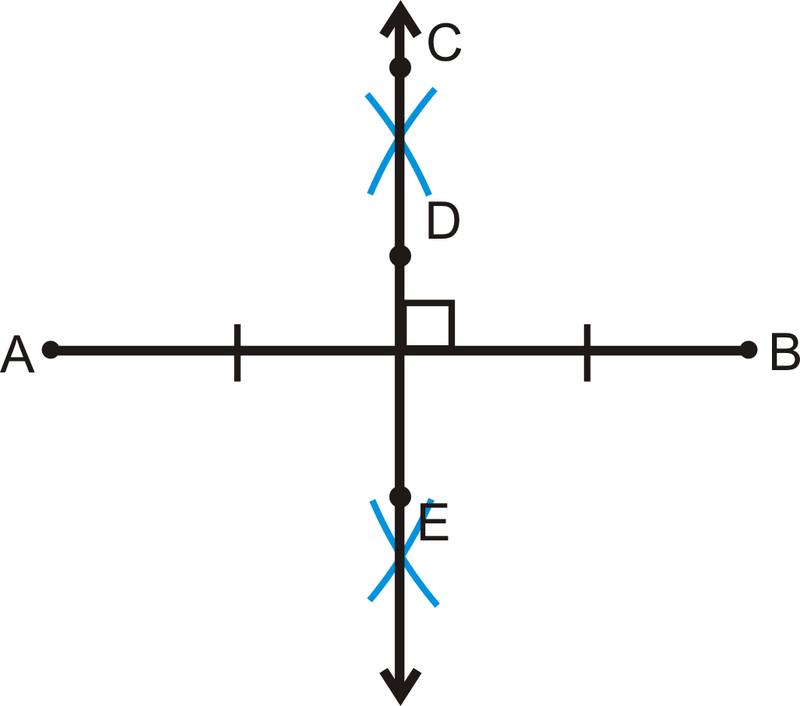
::直直直下两侧区定理

A perpendicular bisector is a line that intersects a line segment at its midpoint and is perpendicular to that line segment, as shown in the construction below.
::如下文的构造所示,直径直径直径直径直径直,中间线直径直,与直线直径直径直径直,直径直径直,直径中点直线直径直,直线直径直直直直,直径直直直直直直,直线直线直径直,直线直径直直直直直直,直线直径直直直直直直直直直直直直直直直直直直线直线直线直线直线直线直线直线直线,直线直线直线直线直线直线直线直线直线直线直线直线,直线直线直线直线直线直线直线直线。

One important property related to perpendicular bisectors is that if a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. This is called the Perpendicular Bisector Theorem .
::与直角两分区有关的一个重要属性是,如果一个点位于某一段的直角两分区,则与该段端点的距离相当,即所谓的直角两分区定理。

If $\begin{aligned} \overset{\leftrightarrow}{C D} ⊥ \bar{A B} \end{aligned}$ and $\begin{aligned} A D = D B \end{aligned}$ , then $\begin{aligned} A C = C B \end{aligned}$ .
::如果CDAB和AD=DB,那么AC=CB。

In addition to the Perpendicular Bisector Theorem, the converse is also true.
::除了直角两侧部分的理论外,反之亦然。

Perpendicular Bisector Theorem Converse : If a point is equidistant from the endpoints of a segment, then the point is on the perpendicular bisector of the segment.
::直角双向线段的理论反面:如果某一点与某一段的端点相距相等,则该点与该段的直角对角线对等。

Using the picture above: If $\begin{aligned} A C = C B \end{aligned}$ , then $\begin{aligned} \overset{\leftrightarrow}{C D} ⊥ \bar{A B} \end{aligned}$ and $\begin{aligned} A D = D B \end{aligned}$ .
::使用上面的照片:如果AC=CB,那么CDAB和AD=DB。

When we construct perpendicular bisectors for the sides of a triangle , they meet in one point. This point is called the circumcenter of the triangle.
::当我们为三角形的两侧建造垂直的双向区段时, 它们会在一个点相交。这个点被称为三角形的周围点。

What if you were given $\begin{aligned} △ F G H \end{aligned}$ and told that $\begin{aligned} \overset{\leftrightarrow}{G J} \end{aligned}$ was the perpendicular bisector of $\begin{aligned} \bar{F H} \end{aligned}$ ? How could you find the length of $\begin{aligned} F G \end{aligned}$ given the length of $\begin{aligned} G H \end{aligned}$ ?
::如果你们被告知GJ是FH的直肠两侧部分呢?鉴于GH的长度,你怎么能找到FG的长度?

Examples
::实例

Example 1
::例1

$\begin{aligned} \overset{\leftrightarrow}{O Q} \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{M P} \end{aligned}$ .
::O是国会议员的直角双侧部分。

Which line segments are equal? Find $\begin{aligned} x \end{aligned}$ . Is $\begin{aligned} L \end{aligned}$ on $\begin{aligned} \overset{\leftrightarrow}{O Q} \end{aligned}$ ? How do you know?
::哪个线段相等? 查找 x. L 是 O 吗? 你怎么知道 ?

$\begin{aligned} M L = L P, M O = O P \end{aligned}$ , and $\begin{aligned} M Q = Q P \end{aligned}$ .
::ML=LP,MO=OP,和MP。

\begin{aligned} 4 x + 3 & = 11 \\ 4 x & = 8 \\ x & = 2 \end{aligned}

::4x+3=114x=8x=2

Yes, $\begin{aligned} L \end{aligned}$ is on $\begin{aligned} \overset{\leftrightarrow}{O Q} \end{aligned}$ because $\begin{aligned} M L = L P \end{aligned}$ (the Perpendicular Bisector Theorem Converse).
::是的,L在O上,因为 ML=LP(直角双向线段理论交汇)

Example 2
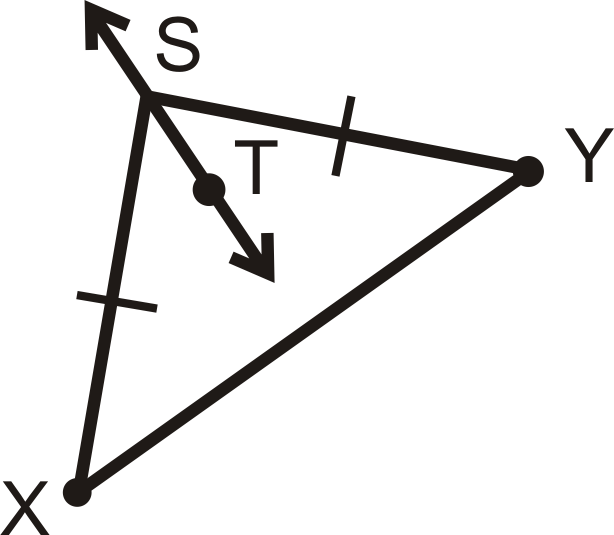
::例2

Determine if $\begin{aligned} \overset{\leftrightarrow}{S T} \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{X Y} \end{aligned}$ . Explain why or why not.
::确定 ST 是否 XY 的垂直双向区块。请解释原因或原因。

$\begin{aligned} \overset{\leftrightarrow}{S T} \end{aligned}$ is not necessarily the perpendicular bisector of $\begin{aligned} \bar{X Y} \end{aligned}$ because not enough information is given in the diagram . There is no way to know from the diagram if $\begin{aligned} \overset{\leftrightarrow}{S T} \end{aligned}$ will extend to make a right angle with $\begin{aligned} \bar{X Y} \end{aligned}$ .
::STQQ 不一定是 XY 的垂直双向区块, 因为图中没有给出足够的信息。无法从图中知道 STQQ 是否将扩展到 XY 右角度。

Example 3
::例3

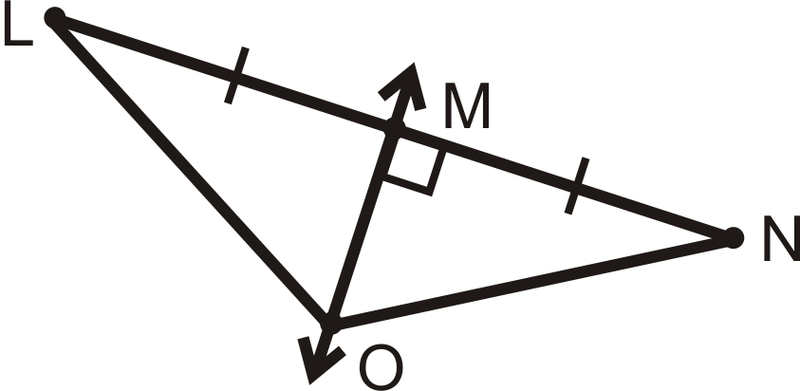
If $\begin{aligned} \overset{\leftrightarrow}{M O} \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{L N} \end{aligned}$ and $\begin{aligned} L O = 8 \end{aligned}$ , what is $\begin{aligned} O N \end{aligned}$ ?
::如果MO是LN和LO=8的直肠两侧部分,

By the Perpendicular Bisector Theorem, $\begin{aligned} L O = O N \end{aligned}$ . So, $\begin{aligned} O N = 8 \end{aligned}$ .
::以直角两侧的定理盟誓,

Example 4
::例4

Find $\begin{aligned} x \end{aligned}$ and the length of each segment.
::查找 x 和每个段的长度。

$\begin{aligned} \overset{\leftrightarrow}{W X} \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{X Z} \end{aligned}$ and from the Perpendicular Bisector Theorem $\begin{aligned} W Z = W Y \end{aligned}$ .
::WX是XZ的直角对角部分和直角对角对角部分的理论WZWY

\begin{aligned} 2 x + 11 & = 4 x - 5 \\ 16 & = 2 x \\ 8 & = x \end{aligned}

::2x+11=4x-516=2x8=x

$\begin{aligned} W Z = W Y = 2 (8) + 11 = 16 + 11 = 27 \end{aligned}$ .
::WWY=2(8)+11=16+11=27。

Example 5
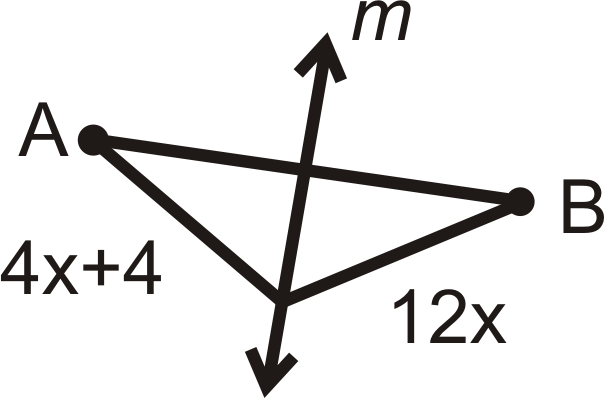
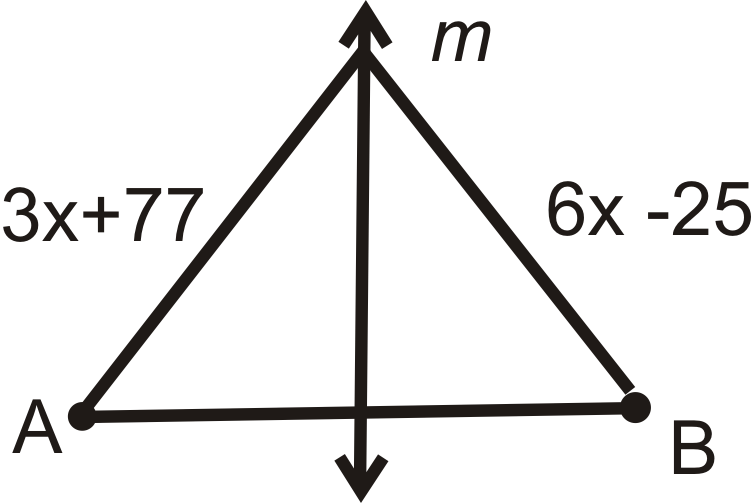
::例5

Find the value of $\begin{aligned} x \end{aligned}$ . $\begin{aligned} m \end{aligned}$ is the perpendicular bisector of $\begin{aligned} A B \end{aligned}$ .
::查找 x. m 值为AB 的垂直双向分形。

By the Perpendicular Bisector Theorem, both segments are equal. Set up and solve an equation.
::以直角双向线段定理为单位,两个区段均相等。设置并解析一个方程。

\begin{aligned} 3 x - 8 & = 2 x \\ x & = 8 \end{aligned}

::3x-8=2xx=8

Review
::回顾

For questions 1-4, find the value of $\begin{aligned} x \end{aligned}$ . $\begin{aligned} m \end{aligned}$ is the perpendicular bisector of $\begin{aligned} A B \end{aligned}$ .
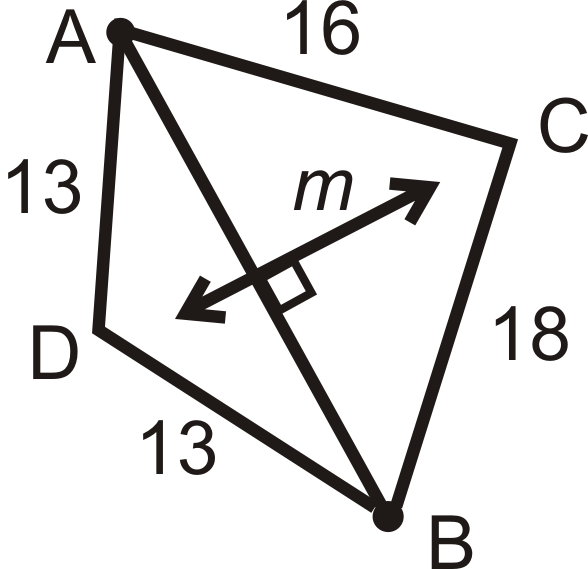
::对于问题1-4,发现x.m的值是AB的垂直分形。

$\begin{aligned} m \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{A B} \end{aligned}$ . Also imagine that point $\begin{aligned} M \end{aligned}$ is the intersection of line $\begin{aligned} m \end{aligned}$ and $\begin{aligned} \bar{A B .} \end{aligned}$
::m 是AB的垂直两侧区段。想象一下 M 点是线m 和 AB 的交叉点。

List all the congruent segments.
::列出所有相匹配的区段。

Is $\begin{aligned} C \end{aligned}$ on $\begin{aligned} m \end{aligned}$ ? Why or why not?
::C在M上吗为什么不行

Is $\begin{aligned} D \end{aligned}$ on $\begin{aligned} m \end{aligned}$ ? Why or why not?
::为什么还是为什么?

For Question 8, determine if $\begin{aligned} \overset{\leftrightarrow}{S T} \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{X Y} \end{aligned}$ . Explain why or why not.
::对于问题8,请确定ST是否XY的垂直两侧部分。请解释原因或原因。

In what type of triangle will all perpendicular bisectors pass through vertices of the triangle?
::在什么样的三角形中,所有垂直的双形区段都会穿过三角形的顶端?

Fill in the blanks of the proof of the Perpendicular Bisector Theorem.
::填上直角两侧定理的空格

Given : $\begin{aligned} \overset{\leftrightarrow}{C D} \end{aligned}$ is the perpendicular bisector of $\begin{aligned} \bar{A B} \end{aligned}$
::缩略语:CD是AB(AB)的直角双侧部分。

Prove : $\begin{aligned} \bar{A C} ≅ \bar{C B} \end{aligned}$
::证明:AC CC CB

*Statement*	*Reason*
1.	1.
2. $\begin{aligned} D \end{aligned}$ is the midpoint of $\begin{aligned} \bar{A B} \end{aligned}$	2.
3.	3. Definition of a midpoint
4. $\begin{aligned} ∠ C D A \end{aligned}$ and $\begin{aligned} ∠ C D B \end{aligned}$ are right angles	4.
5. $\begin{aligned} ∠ C D A ≅ ∠ C D B \end{aligned}$	5.
6.	6. Reflexive PoC
7. $\begin{aligned} △ C D A ≅ △ C D B \end{aligned}$	7.
8. $\begin{aligned} \bar{A C} ≅ \bar{C B} \end{aligned}$	8.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

垂直两侧部门

Perpendicular Bisector Theorem ::直直直下两侧区定理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源