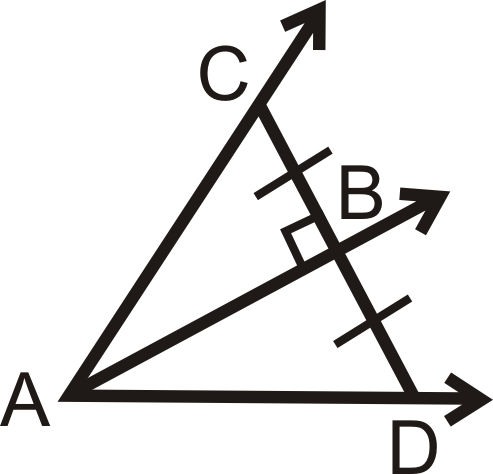
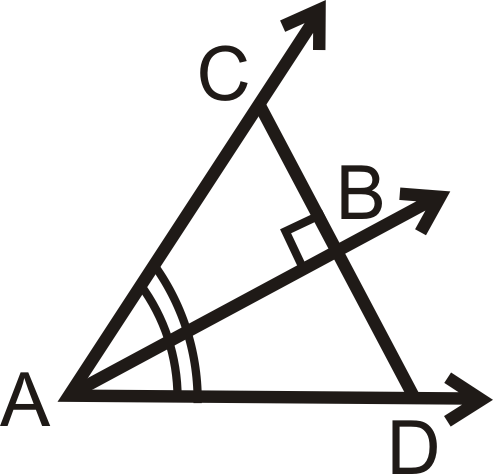
课程： 5.3 三角形中的角分区

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

三角形中的角角分区

Angle Bisector Theorem
::角双两区定理

An angle bisector cuts an angle exactly in half. One important property of angle bisectors is that if a point is on the bisector of an angle, then the point is equidistant from the sides of the angle. This is called the Angle Bisector Theorem .
::角对角对角将角切成两半。角对角对角的一个重要属性是,如果角对角对角对角对角对角,那么对角对角对角的对角就是等的。这叫做角对角对角的对角理论。

In other words, if $\begin{align*}\overrightarrow{BD}\end{align*}$ bisects $\begin{align*}\angle ABC, \ \overrightarrow{BA} \perp \overline{FD}\end{align*}$ , and, $\begin{align*}\overrightarrow{BC} \perp \overline{DG}\end{align*}$ then $\begin{align*}FD = DG\end{align*}$ .
::换句话说,如果"BD"两部分是"ABC",那么"BC"和"BC",然后是"DG"

The converse of this theorem is also true.
::这一定理的反义也是对的。

Angle Bisector Theorem Converse : If a point is in the interior of an angle and equidistant from the sides, then it lies on the bisector of that angle.
::角双点理论对立:如果一个点在角的内部,而距离两侧的等距,那么它就在于角的两边。

When we construct angle bisectors for the angles of a triangle , they meet in one point. This point is called the incenter of the triangle.
::当我们为三角形角度建造角角对角区域时, 它们会在一个点相交。这个点被称为三角形的中间点。

What if you were told that $\begin{align*}\overrightarrow{GJ}\end{align*}$ is the angle bisector of $\begin{align*}\angle FGH\end{align*}$ ? How would you find the length of $\begin{align*}FJ\end{align*}$ given the length of $\begin{align*}HJ\end{align*}$ ?
::如果有人告诉你"GJ"是"FGH"的双角部分呢?如果"GJ"是"FGH"的角,你如何找到"FJ"的长度?因为"HJ"的长度,你如何找到"FJ"的长度?

Examples
::实例

Example 1
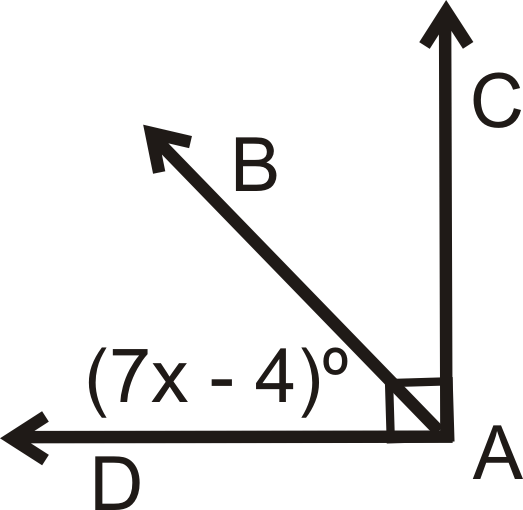
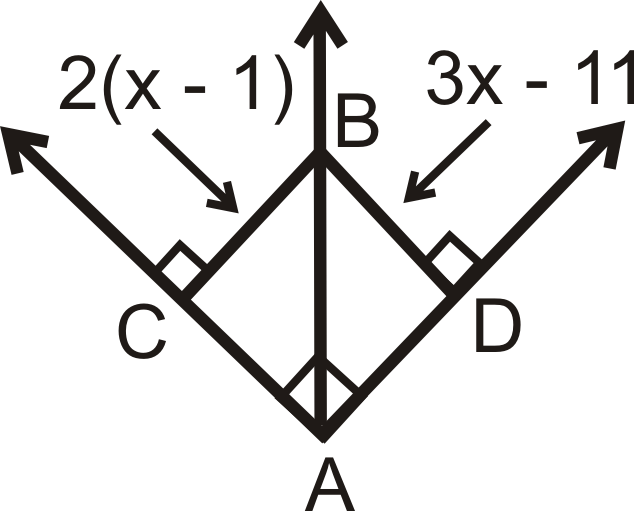
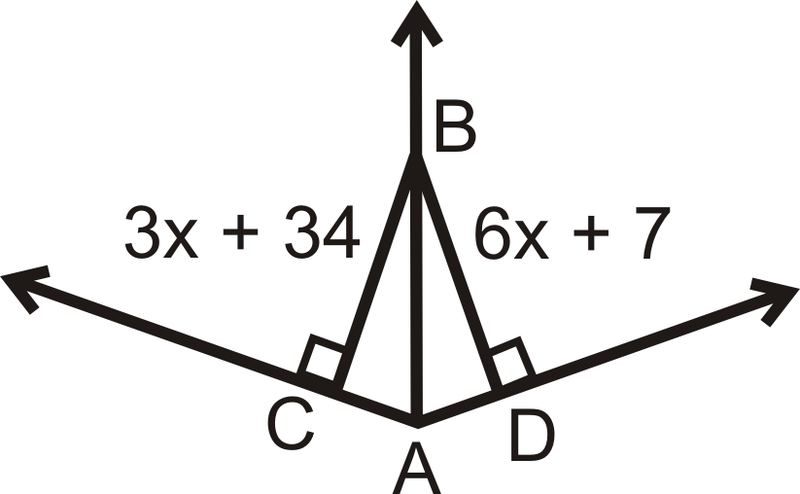
::例1

Is there enough information to determine if $\begin{align*}\overrightarrow{A B}\end{align*}$ is the angle bisector of $\begin{align*}\angle CAD\end{align*}$ ? Why or why not?
::是否有足够的信息来确定“AB”是否是“CAD”的分角部分?为什么或为什么不是?

No because $\begin{align*}B\end{align*}$ is not necessarily equidistant from $\begin{align*}\overline{AC}\end{align*}$ and $\begin{align*}\overline{AD}\end{align*}$ . We do not know if the angles in the diagram are right angles.
::不,因为比斯和阿联酋的距离不一定相等。我们不知道图表中的角度是否正确。

Example 2
::例2

A $\begin{align*} 108^\circ\end{align*}$ angle is bisected. What are the measures of the resulting angles?
::A 108 角度是双切的。由此得出的角度的量度是多少 ?

We know that to bisect means to cut in half, so each of the resulting angles will be half of $\begin{align*}108\end{align*}$ . The measure of each resulting angle is $\begin{align*}54^\circ\end{align*}$ .
::我们知道,将两条分割成两条意味着将两条分割成两条,因此所产生的角度各为108个角度的一半。衡量每个结果角度的尺度是54。

Example 3
::例3

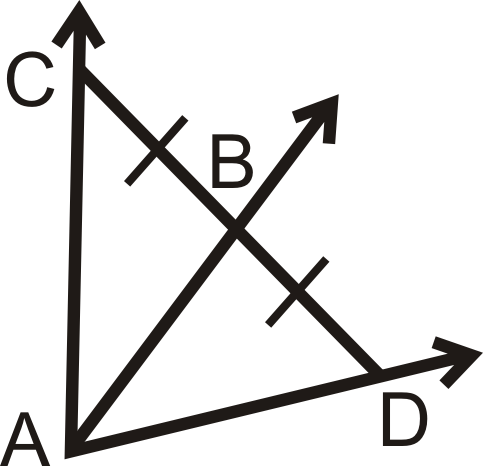
Is $\begin{align*}Y\end{align*}$ on the angle bisector of $\begin{align*}\angle XWZ\end{align*}$ ?
::Y在ZXWZ的角上吗?

If $\begin{align*}Y\end{align*}$ is on the angle bisector, then $\begin{align*}XY = YZ\end{align*}$ and both segments need to be perpendicular to the sides of the angle. From the markings we know $\begin{align*}\overline{XY} \perp \overrightarrow{WX}\end{align*}$ and $\begin{align*}\overline{ZY} \perp \overrightarrow{WZ}\end{align*}$ . Second, $\begin{align*}XY = YZ = 6\end{align*}$ . So, yes, $\begin{align*}Y\end{align*}$ is on the angle bisector of $\begin{align*}\angle XWZ\end{align*}$ .
::如果Y在角角两侧, 那么XY=YZ 和两个区段都必须与角的两侧垂直。从我们所知道的标记中, 我们知道' XY'WX 和 'YWZ. 第二, XY=Y. 6。所以, 是的, Y在 QXWZ 的角两侧。

Example 4
::例4

$\begin{align*}\overrightarrow{MO}\end{align*}$ is the angle bisector of $\begin{align*}\angle LMN\end{align*}$ . Find the measure of $\begin{align*}x\end{align*}$ .
::MO 是 QLMN 的角。查找 x 的度量。

$\begin{align*}LO = ON\end{align*}$ by the Angle Bisector Theorem.
::LOON的角双区定理。

$\begin{align*}4x - 5 &= 23\\ 4x &= 28\\ x &=7\end{align*}$
::4x-5=234x=28x=7

Example 5
::例5

$\begin{align*}\overrightarrow{AB}\end{align*}$ is the angle bisector of $\begin{align*}\angle CAD\end{align*}$ . Solve for the missing variable.
::AB 是 QCAD 的角。解决缺失变量。

$\begin{align*}CB=BD\end{align*}$ by the Angle Bisector Theorem, so we can set up and solve an equation for $\begin{align*}x\end{align*}$ .
::CB = BD by the angle Bishain by the Bishain by the angle Bishain by Theorem, 所以我们可以设置并解析 x 的方程式。

$\begin{align*} x+7 &=2(3x-4)\\ x+7 &=6x-8\\ 15 &=5x\\ x &=3 \end{align*}$
::x7=2(3x-4)x+7=6x-815=5xx=3

Review
::回顾

For questions 1-4, $\begin{align*}\overrightarrow{AB}\end{align*}$ is the angle bisector of $\begin{align*}\angle CAD\end{align*}$ . Solve for the missing variable.
::对于问题1-4, AB是 QCAD 的角角对角。解决缺失变量。

In what type of triangle will all angle bisectors pass through vertices of the triangle?
::在什么样的三角形中, 所有角的双分区都会通过三角形的顶端?

What is another name for the angle bisectors of the vertices of a square?
::方形顶端的角分区别又叫什么来着 ?

Bisect a square with a diagonal. How many triangles do you have and what type of triangles are they?
::以对角分割方形。您有多少三角形, 以及三角形的类型 ?

Fill in the blanks in the Angle Bisector Theorem Converse.
::填充角小区理论对讲中的空白。

Given : $\begin{align*}\overline{AD} \cong \overline{DC}\end{align*}$ , such that $\begin{align*}AD\end{align*}$ and $\begin{align*}DC\end{align*}$ are the shortest distances to $\begin{align*}\overrightarrow{BA}\end{align*}$ and $\begin{align*}\overrightarrow{BC}\end{align*}$
::给定:AD'DDC,所以AD和DC 距离BA和BC最短的距离

Prove : $\begin{align*}\overrightarrow{BD}\end{align*}$ bisects $\begin{align*}\angle ABC\end{align*}$
::证明: BD 双形 ABC

*Statement*	*Reason*
1.	1.
2.	2. The shortest distance from a point to a line is perpendicular.
3. $\begin{align}\angle DAB\end{align}$ and $\begin{align}\angle DCB\end{align}$ are right angles	3.
4. $\begin{align}\angle DAB \cong \angle DCB\end{align}$	4.
5. $\begin{align}\overline{BD} \cong \overline{BD}\end{align}$	5.
6. $\begin{align}\triangle ABD \cong \triangle CBD\end{align}$	6.
7.	7. CPCTC
8. $\begin{align}\overrightarrow{B D}\end{align}$ bisects $\begin{align}\angle ABC\end{align}$	8.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

三角形中的角角分区

Angle Bisector Theorem ::角双两区定理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源