1.17 三角函数和旋转角度

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三角函数和旋转角度

  Collapse Expand

  三角函数和旋转角度

  播放段落

  You've been working hard in your math class, and are getting to be quite the expert on trig functions. Then one day your friend, who is a year ahead of you in school, approaches you.
  ::你一直在数学课上辛勤工作, 并且越来越擅长三角函数。然后有一天,你朋友,比学校早一年, 接近你。

  播放段落

  "So, you're doing pretty well in math? And you're good with trig functions?" he asks with a smile.
  ::"那么,你数学表现很好吗?你擅长三角函数?" 他笑着问

  播放段落

  "Yes," you reply confidently. "I am."
  ::"是的,"你自信地回答 "我是"

  播放段落

  "Alright, then what's the sine of $\begin{array}{r}{150}^{\circ }\end{array}$ ?" he asks.
  ::"好吧,那么150的正弦是什么?" 他问。

  播放段落

  "What? That doesn't make sense. No right triangle has an angle like that, so there's no way to define that function!" you say.
  ::"什么?这说不通。没有右三角形有这样的角度,所以没有办法定义这个功能!"你说。

  播放段落

  Your friend laughs. "As it turns out, it is quite possible to have trig functions of angles greater than $\begin{array}{r}{90}^{\circ }\end{array}$ ."
  ::你的朋友笑了。 “事实证明, 角的三角函数 很可能大于90英寸。”

  播放段落

  Is your friend just playing a joke on you, or does he mean it? Can you actually calculate $\begin{array}{r}\sin {150}^{\circ }\end{array}$ ?
  ::你的朋友是在跟你开玩笑,还是他是认真的?

  播放段落

  Angles of Rotation and Trigonometric Functions
  ::旋转和三角函数的角

  播放段落

  Just as it is possible to define the six trigonometric functions for angles in right triangles, we can also define the same functions in terms of angles of rotation.
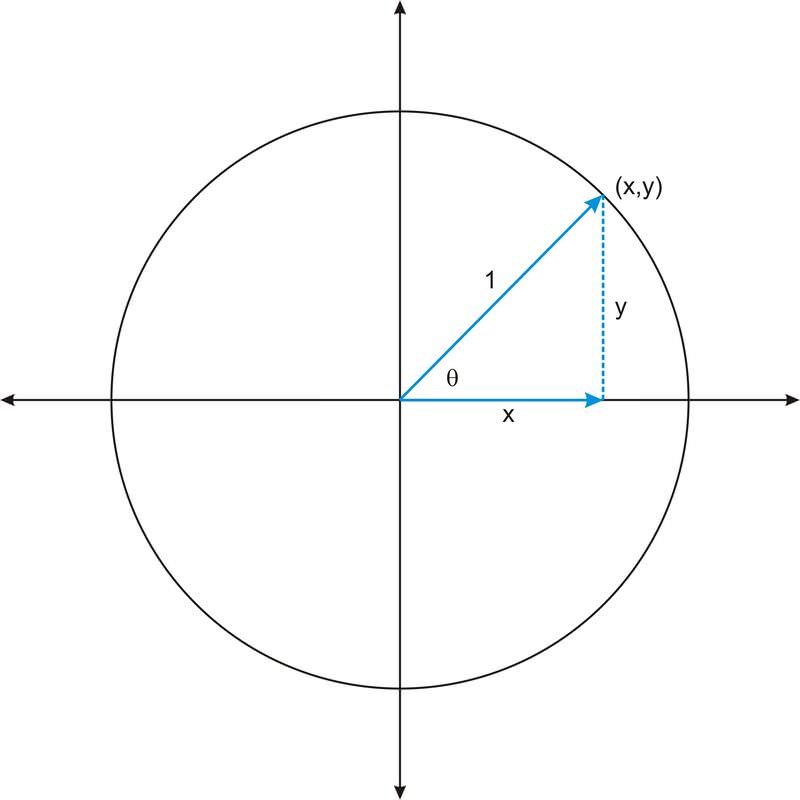
  ::正如有可能界定右三角形角度的六个三角函数一样,我们也可以定义旋转角度的相同函数。

  播放段落

  Consider an angle in standard position , whose terminal side intersects a circle of radius $\begin{array}{r}r\end{array}$ . We can think of the radius as the hypotenuse of a right triangle:
  ::以标准位置考虑一个角度, 其终点侧交叉半径圆 r。 我们可以将半径视为右三角形的下限 :

  

  播放段落

  The point $\begin{array}{r}(x,y)\end{array}$ where the terminal side of the angle intersects the circle tells us the lengths of the two legs of the triangle. Now, we can define the trigonometric functions in terms of $\begin{array}{r}x,y\end{array}$ , and $\begin{array}{r}r\end{array}$ :
  ::角的终点侧交叉圆的点 (x,y) 。 圆形的终点侧告诉我们三角形两腿的长度。 现在, 我们可以用 x, y 和 r 来定义三角函数 :

  播放段落

  $$\begin{array}{rlr}\cos \theta =\frac{x}{r}& & \sec \theta =\frac{r}{x}\\ \sin \theta =\frac{y}{r}& & \csc \theta =\frac{r}{y}\\ \tan \theta =\frac{y}{x}& & \cot \theta =\frac{x}{y}\end{array}$$

  
  ::

  播放段落

  And, we can extend these functions to include non-acute angles.
  ::而且,我们可以将这些功能扩大到包括非加速角度。

  播放段落

  Consider an angle in standard position, such that the point $\begin{array}{r}(x,y)\end{array}$ on the terminal side of the angle is a point on a circle with radius 1.
  ::在标准位置中考虑一个角度,使角度末端的点(x,y)是圆圆的点,半径为1。

  

  播放段落

  This circle is called the unit circle . With $\begin{array}{r}r=1\end{array}$ , we can define the trigonometric functions in the unit circle:
  ::此圆称为单位圆。 使用 r=1, 我们可以定义单位圆的三角函数 :

  播放段落

  $$\begin{array}{rlrl}\cos \theta & =\frac{x}{r}=\frac{x}{1}=x& & \sec \theta =\frac{r}{x}=\frac{1}{x}\\ \sin \theta & =\frac{y}{r}=\frac{y}{1}=y& & \csc \theta =\frac{r}{y}=\frac{1}{y}\\ \tan \theta & =\frac{y}{x}& & \cot \theta =\frac{x}{y}\end{array}$$

  
  ::cosaxr=x1=xsecrx=1xsinyr=y1=yscry=1yytanyxcotxyyyyyy

  播放段落

  Notice that in the unit circle, the of an angle are the $\begin{array}{r}y\end{array}$ and $\begin{array}{r}x\end{array}$ coordinates of the point on the terminal side of the angle. Now we can find the values of the trigonometric functions of any angle of rotation, even the quadrantal angles, which are not angles in triangles.
  ::请注意, 在单位圆中, 一个角度是角度末端点的 Y 和 x 坐标。 现在我们可以找到任何旋转角度的三角函数值, 甚至是四边角, 它们不是三角形中的角 。

  

  播放段落

  We can use the figure above to determine values of the trig functions for the quadrantal angles. For example, $\begin{array}{r}\sin {90}^{\circ }=y=1\end{array}$ .
  ::我们可以使用上图来确定四角角的三角函数值。 例如, sin90y=1 。

  播放段落

  Determining the Value of Trigonometric Functions 
  ::确定三角函数的数值

  播放段落

  1. Determine the values of the six trigonometric functions. 
  ::1. 确定六个三角函数的数值。

  播放段落

  The point (-3, 4) is a point on the terminal side of an angle in standard position. Determine the values of the six trigonometric functions of the angle.
  ::点( 3, 4) 是标准位置中角的终点边上的点。 确定角的六个三角函数的值 。

  播放段落

  Notice that the angle is more than 90 degrees, and that the terminal side of the angle lies in the second quadrant. This will influence the signs of the trigonometric functions.
  ::注意角值超过90度, 角的末端在第二个象限内。 这将影响三角函数的符号 。

  

  播放段落

  $$\begin{array}{rlrl}\cos \theta & =\frac{-3}{5}& & \sec \theta =\frac{5}{-3}\\ \sin \theta & =\frac{4}{5}& & \csc \theta =\frac{5}{4}\\ \tan \theta & =\frac{4}{-3}& & \cot \theta =\frac{-3}{4}\end{array}$$

  
  ::5 -3sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\343434\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Notice that the value of $\begin{array}{r}r\end{array}$ depends on the coordinates of the given point. You can always find the value of $\begin{array}{r}r\end{array}$ using the . However, often we look at angles in a circle with radius 1. As you can see, doing this allows us to simplify the definitions of the trig functions.
  ::请注意 r 值取决于给定点的坐标。 您总是可以找到 r 值 。 但是, 我们经常在圆圈中查看圆半径 1 的角, 您可以看到, 这样做可以简化三角函数的定义 。

  播放段落

  2. Use the unit circle above to find the value of $\begin{array}{r}\cos {90}^{\circ }\end{array}$
  ::2. 使用上面的单位圆来找到cos 90 的值。

  播放段落

    $\begin{array}{r}\cos {90}^{\circ }=0\end{array}$
  ::COS900

  播放段落

  The ordered pair for this angle is (0, 1). The cosine value is the $\begin{array}{r}x\end{array}$ coordinate, .
  ::此角度的订购对数是 (0, 1) 。 余弦值是 x 坐标 。

  播放段落

  3. Use the unit circle above to find the value of $\begin{array}{r}\cot {180}^{\circ }\end{array}$
  ::3. 使用上面的单位圆来找到COTQ180的值。

  播放段落

    $\begin{array}{r}\cot {180}^{\circ }\end{array}$ is undefined
  ::comt 180 尚未定义

  播放段落

  The ordered pair for this angle is (-1, 0). The ratio $\begin{array}{r}\frac{x}{y}\end{array}$ is $\begin{array}{r}\frac{-1}{0}\end{array}$ , which is undefined.
  ::此角度的定序对数是 (-1, 0) 。 比例xy 是- 10, 未定义 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if you can actually calculate  $\begin{array}{r}\sin {150}^{\circ }\end{array}$ .
  ::之前有人问过你是否真的算得上sin 150 。

  播放段落

  Since you now know that it is possible to apply trigonometric functions to angles greater than $\begin{array}{r}{90}^{\circ }\end{array}$ , you can calculate the $\begin{array}{r}\sin {150}^{\circ }\end{array}$ . The easiest way to do this without difficulty is to consider that an angle of $\begin{array}{r}{150}^{\circ }\end{array}$ is in the same position as $\begin{array}{r}{30}^{\circ }\end{array}$ , except it's in the second quadrant. This means that it has the same "x" and "y" values as $\begin{array}{r}{30}^{\circ }\end{array}$ , except that the "x" value is negative.
  ::既然您现在知道可以对大于 90 的角应用三角函数, 您可以计算 sin 150 。 最容易的方法是考虑 150 的角与 30 相同, 但它在第二个象限中除外。 这意味着它的“ x” 和“y” 值与 30 相同, 但“ x” 值为负值 。

  播放段落

  Therefore,
  ::因此,

  播放段落

  $\begin{array}{r}\sin {150}^{\circ }=\frac{1}{2}\end{array}$
  ::问题150**12

  播放段落

  Use this figure:
  ::使用此图 :

  

  播放段落

  to answer the following  examples.
  ::回答以下例子。

  播放段落

  Example 2
  ::例2

  播放段落

  Find $\begin{array}{r}\cos \theta \end{array}$ on the circle above.
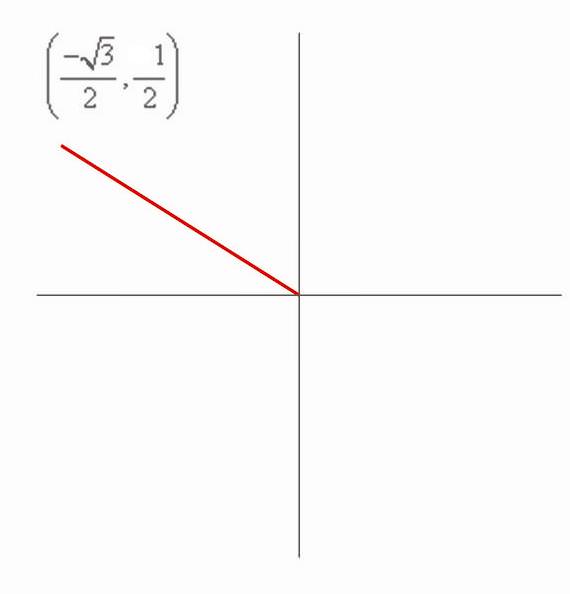
  ::在上面的圆上查找 COs 。

  播放段落

  We can see from the "x" and "y" axes that the "x" coordinate is $\begin{array}{r}\frac{-\sqrt{3}}{2}\end{array}$ , the "y" coordinate is $\begin{array}{r}\frac{1}{2}\end{array}$ , and the hypotenuse has a length of 1. This means that the cosine function is:
  ::我们从“x”和“y”轴可以看出,“x”坐标是-32,“y”坐标是12,而“y”坐标是1,这意味着余弦函数是:

  播放段落

  $$\begin{array}{r}\cos \theta =\frac{adjacent}{hypotenuse}=\frac{\frac{-\sqrt{3}}{2}}{1}=\frac{-\sqrt{3}}{2}\end{array}$$

  
  ::近邻的海滨海 321 32

  播放段落

  Example 3
  ::例3

  播放段落

  Find $\begin{array}{r}\cot \theta \end{array}$ on the circle above.
  ::在上面的圆上找到 cot 。

  播放段落

  We know that $\begin{array}{r}\cot =\frac{1}{\tan }=\frac{1}{\frac{opposite}{adjacent}}=\frac{adjacent}{opposite}\end{array}$ . The adjacent side to $\begin{array}{r}\theta \end{array}$ in the circle is $\begin{array}{r}\frac{-\sqrt{3}}{2}\end{array}$ and the opposite side is $\begin{array}{r}\frac{1}{2}\end{array}$ . Therefore,
  ::我们知道,在圆圈中,的邻接面是-32,对面是-12。

  播放段落

  $$\begin{array}{r}\cot \theta =\frac{\frac{-\sqrt{3}}{2}}{\frac{1}{2}}=-\sqrt{3}\end{array}$$

  
  ::二氧化碳3212%3

  播放段落

  Example 4
  ::例4

  播放段落

  Find $\begin{array}{r}\csc \theta \end{array}$ on the circle above.
  ::在上面的圆上找到 csc 。

  播放段落

   We know that $\begin{array}{r}\csc =\frac{1}{\sin }=\frac{1}{\frac{opposite}{hypotenuse}}=\frac{hypotenuse}{opposite}\end{array}$ . The opposite side to $\begin{array}{r}\theta \end{array}$ in the circle is $\begin{array}{r}\frac{1}{2}\end{array}$ and the hypotenuse is 1. Therefore,
  ::我们知道,Csc=1sin=1对面的日间聚苯乙烯=1对面的日间聚苯乙烯=-在圆圈中,对面的一面是12,下限是1,因此,

  播放段落

  $$\begin{array}{r}\csc \theta =\frac{hypotenuse}{opposite}=\frac{1}{\frac{1}{2}}=2\end{array}$$

  
  ::csc-hypotenus 日光观测站=1112=2

  播放段落

  Review
  ::回顾

  播放段落

  Find the values of the six trigonometric functions for each angle below.
  ::查找以下每个角度的六个三角函数的值。

  1. $\begin{array}{r}{0}^{\circ }\end{array}$
  2. $\begin{array}{r}{90}^{\circ }\end{array}$
  3. $\begin{array}{r}{180}^{\circ }\end{array}$
  4. $\begin{array}{r}{270}^{\circ }\end{array}$
  播放段落
  5. Find the sine of an angle that goes through the point $\begin{array}{r}(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\end{array}$ .
     ::找到一个通过点(22,22)的角的正弦值。
  播放段落
  6. Find the cosine of an angle that goes through the point $\begin{array}{r}(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\end{array}$ .
     ::找到一个穿过点(22,22)角角的余弦。
  播放段落
  7. Find the tangent of an angle that goes through the point $\begin{array}{r}(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\end{array}$ .
     ::找到一个穿过点(22,22)的角的正切值。
  播放段落
  8. Find the secant of an angle that goes through the point $\begin{array}{r}(-\frac{\sqrt{3}}{2},\frac{1}{2})\end{array}$ .
     ::找到一个经过点角(-32,12)角的分离点。
  播放段落
  9. Find the cotangent of an angle that goes through the point $\begin{array}{r}(-\frac{\sqrt{3}}{2},-\frac{1}{2})\end{array}$ .
     ::找到一个贯穿点(-32,-12)的角的相切性(-32,-12)。
  播放段落
  10. Find the cosecant of an angle that goes through the point $\begin{array}{r}(\frac{\sqrt{3}}{2},\frac{1}{2})\end{array}$ .
      ::找到一个经过点( 32, 12) 角的余生。
  播放段落
  11. Find the sine of an angle that goes through the point $\begin{array}{r}(\frac{1}{2},-\frac{\sqrt{3}}{2})\end{array}$ .
      ::找到一个穿过点( 12,-32) 角的正弦值 。
  播放段落
  12. Find the cosine of an angle that goes through the point $\begin{array}{r}(-\frac{\sqrt{3}}{2},\frac{1}{2})\end{array}$ .
      ::找到一个贯穿点(-32,12)角的余弦(- 32,12) 。
  播放段落
  13. The sine of an angle in the first quadrant is $\begin{array}{r}0.25\end{array}$ . What is the cosine of this angle?
      ::第一个象限角的正弦是0.25, 这个角的余弦是什么?
  播放段落
  14. The cosine of an angle in the first quadrant is $\begin{array}{r}0.8\end{array}$ . What is the sine of this angle?
      ::第一个象限中角的余弦是0.8.。 这个角的正弦是什么?
  播放段落
  15. The sine of an angle in the first quadrant is $\begin{array}{r}0.15\end{array}$ . What is the cosine of this angle?
      ::第一个象限中角的正弦值是 0.15。 这个角的余弦是什么 ?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。