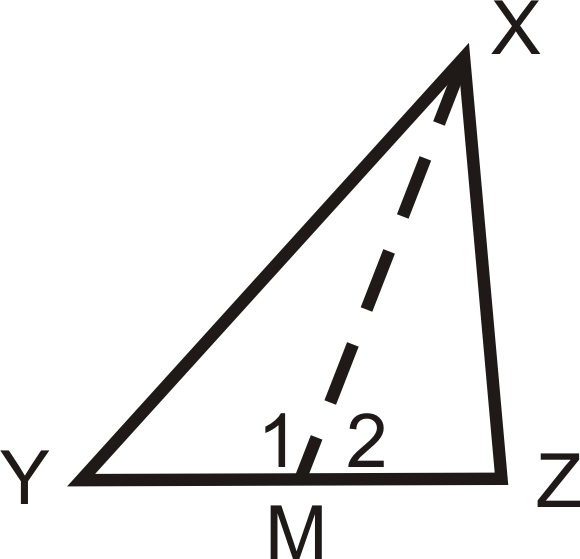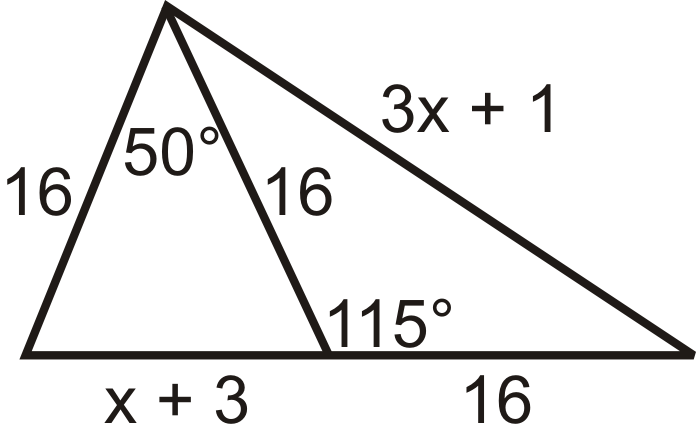5.6 三角形的角和边比较

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 比较三角形中的角和边

  Collapse Expand

  比较三角形中的角和边

  播放段落

  SAS and SSS Inequality Theorems
  ::SAS和SSSS 不平等理论

  播放段落

  Look at the triangle below. The sides of the triangle are given. Can you determine which angle is the largest? The largest angle will be opposite 18 because that is the longest side. Similarly, the smallest angle will be opposite 7, which is the shortest side.
  ::查看下方的三角形。 给定三角形的两边。 您能否确定哪个角最大? 最大角是18对面, 因为那是最长的一面。 同样, 最小角是7对面, 最短的一面是7对面 。

  

  播放段落

  This idea is actually a theorem : If one side of a triangle is longer than another side, then the angle opposite the longer side will be larger than the angle opposite the shorter side.
  ::这个概念实际上是一个理论: 如果三角形的一边比另一边长, 则对面的角会大于对面的角。

  播放段落

  The converse is also true: If one angle in a triangle is larger than another angle in that triangle, then the side opposite the larger angle will be longer than the side opposite the smaller angle.
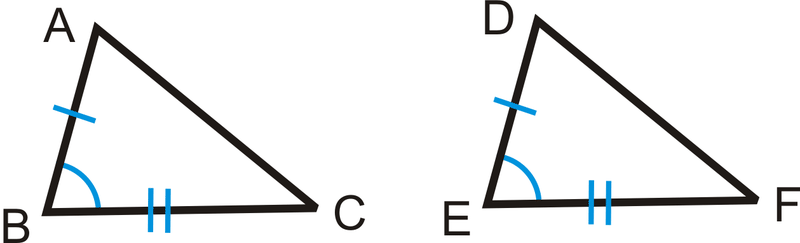
  ::反之亦然:如果三角形中一个角度大于该三角形中另一个角度,则对面的较大角度比对面的角长。

  播放段落

  We can extend this idea into two theorems that help us compare sides and angles in two triangles If we have two congruent triangles $\begin{align*}\triangle ABC\end{align*}$ and $\begin{align*}\triangle DEF\end{align*}$ , marked below:
  ::我们可以把这个想法扩展为两个理论, 帮助我们比较两个三角形的侧面和角度, 如果我们有两个相似的三角形, 即QABC和ZDEF, 标注如下:

  

  播放段落

  Therefore, if $\begin{align*}AB = DE\end{align*}$ , $\begin{align*}BC = EF\end{align*}$ , and $\begin{align*}m \angle B = m \angle E\end{align*}$ , then $\begin{align*}AC = DF\end{align*}$ .
  ::因此,如果AB=DE,BC=EF,MB=mE,那么AC=DF。

  播放段落

  Now, let’s make $\begin{align*}m \angle B > m \angle E\end{align*}$ . Would that make $\begin{align*}AC > DF\end{align*}$ ? Yes. This idea is called the SAS Inequality Theorem .
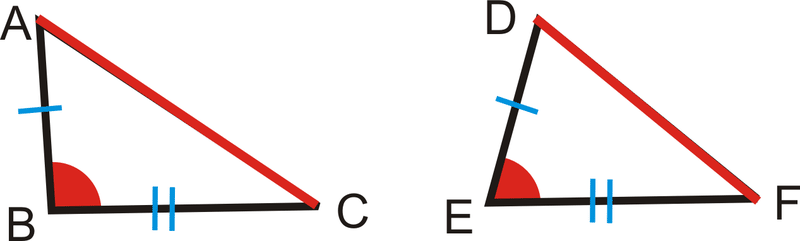
  ::现在,让我们来做 mB'mE。 这样能形成AC>DF吗? 是的。 这个想法叫做SAS不平等理论。

  

  播放段落

  The SAS Inequality Theorem: If two sides of a triangle are congruent to two sides of another triangle, but the included angle of one triangle has greater measure than the included angle of the other triangle, then the third side of the first triangle is longer than the third side of the second triangle.
  ::SAS不平等理论:如果三角形的两面与另一三角形的两面一致,但一个三角形的包含角比另一个三角形的包含角的大小更大,那么第一个三角形的第三面比第二个三角形的第三面长。

  

  播放段落

  If $\begin{align*}\overline{AB} \cong \overline{DE}, \overline{BC} \cong \overline{EF}\end{align*}$ and $\begin{align*}m \angle B > m \angle E\end{align*}$ , then $\begin{align*}\overline{AC} > \overline{DF}\end{align*}$ .
  ::如果AB是,BC是和M'B'ME,那么AC是。

  播放段落

  If we know the third sides as opposed to the angles, the opposite idea is also true and is called the SSS Inequality Theorem .
  ::如果我们了解第三方而不是角度,相反的想法也是真实的,并被称为SSS不平等理论。

  播放段落

  SSS Inequality Theorem: If two sides of a triangle are congruent to two sides of another triangle, but the third side of the first triangle is longer than the third side of the second triangle, then the included angle of the first triangle's two congruent sides is greater in measure than the included angle of the second triangle's two congruent sides.
  ::SSS 不平等理论: 如果三角的两面与另一三角的两面相匹配, 但第一个三角的第三面长于第二个三角的第三面, 那么第一个三角的两面的包含角在数量上大于第二个三角的两面的包含角。

  

  播放段落

  If $\begin{align*}\overline{AB} \cong \overline{DE}, \ \overline{BC} \cong \overline{EF}\end{align*}$ and $\begin{align*}\overline{AC} > \overline{DF}\end{align*}$ , then $\begin{align*}m \angle B > m \angle E\end{align*}$ .
  ::如果AB是,BC是,AC是,然后mB'mE。

  播放段落

  What if you were told that a triangle has sides that measure 3, 4, and 5? How could you determine which of the triangle's angles is largest? Smallest?
  ::如果有人告诉你三角形的边有测量3、4和5的边?你怎么确定三角形的角最大?最小的边?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  If $\begin{align*}\overline{XM}\end{align*}$ is a median of $\begin{align*}\triangle XYZ\end{align*}$ and $\begin{align*}XY > XZ\end{align*}$ , what can we say about $\begin{align*}m \angle 1\end{align*}$ and $\begin{align*}m \angle 2\end{align*}$ ?
  ::如果XM是 XYZ和XY>XZ的中位数,

  

  播放段落

  $\begin{align*}M\end{align*}$ is the midpoint of $\begin{align*}\overline{YZ}\end{align*}$ , so $\begin{align*}YM = MZ\end{align*}$ . $\begin{align*}MX = MX\end{align*}$ by the Reflexive Property and we know $\begin{align*}XY > XZ\end{align*}$ .
  ::M是YZ的中点, 所以YM=MZ. MX=MX在弹性地产旁边,我们认识XY>XZ。

  播放段落

  We can use the SSS Inequality Theorem Converse to say $\begin{align*}m \angle 1 > m \angle 2\end{align*}$ .
  ::我们可以使用 SSS 不平等理论对口 来表示 m1>m2。

  播放段落

  Example 2
  ::例2

  播放段落

  Below is isosceles triangle $\begin{align*}\triangle ABC\end{align*}$ . List everything you can about the sides and angles of the triangle and why.
  ::列出您所能列出的关于三角形的侧面和角度以及原因的所有信息。

  

  播放段落

  $\begin{align*}M\end{align*}$ is the midpoint of $\begin{align*}\overline{YZ}\end{align*}$ , so $\begin{align*}YM = MZ\end{align*}$ . $\begin{align*}MX = MX\end{align*}$ by the Reflexive Property and we know $\begin{align*}XY > XZ\end{align*}$ .
  ::M是YZ的中点, 所以YM=MZ. MX=MX在弹性地产旁边,我们认识XY>XZ。

  播放段落

  $\begin{align*}AB = BC\end{align*}$ because it is given.
  ::AB=BC,因为它是给的。

  播放段落

  $\begin{align*}m \angle A = m \angle C\end{align*}$ because if sides are equal than their opposite angles must be equal..
  ::mA=mC,因为如果两面与其对角相等,则必须相等。

  播放段落

  $\begin{align*}AD < DC\end{align*}$ because $\begin{align*}m \angle ABD < m \angle CBD\end{align*}$ and because of the .
  ::AD<DC因为 mABD <mCBD和因为 。

  播放段落

  Example 3
  ::例3

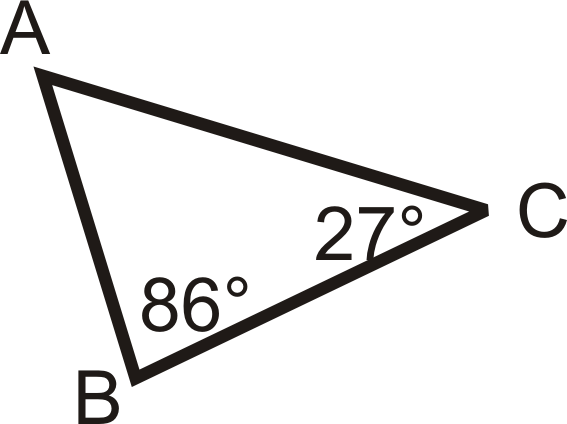
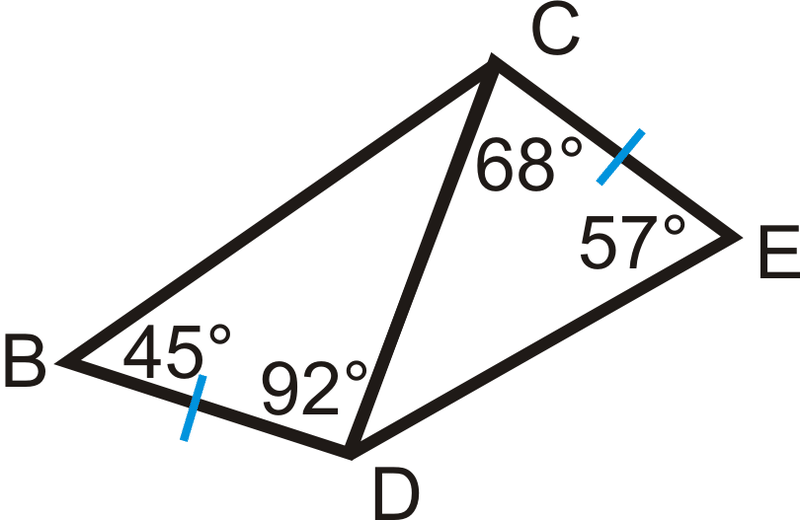
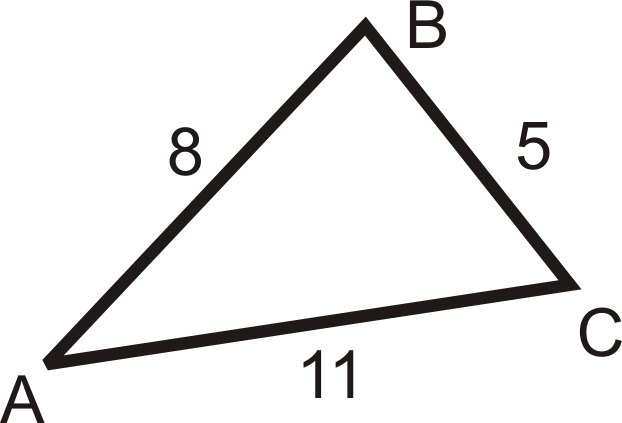
  播放段落

  List the sides in order, from shortest to longest.
  ::按顺序列出双方名单,从最短到最长。

  

  播放段落

  First, find $\begin{align*}m \angle A\end{align*}$ . From the Triangle Sum Theorem:
  ::首先,从三角理论中找到 mA。

  播放段落

  $$\begin{align*}m \angle A + 86^\circ + 27^\circ &= 180^\circ\\ m \angle A &= 67^\circ\end{align*}$$
  ::@A+8627180mA=67

  播放段落

  $\begin{align*}86^\circ\end{align*}$ is the largest angle, so $\begin{align*}AC\end{align*}$ is the longest side. The next angle is $\begin{align*}67^\circ\end{align*}$ , so $\begin{align*}BC\end{align*}$ would be the next longest side. $\begin{align*}27^\circ\end{align*}$ is the smallest angle, so $\begin{align*}AB\end{align*}$ is the shortest side. In order, the answer is: $\begin{align*}AB, \ BC, \ AC\end{align*}$ .
  ::86 是最大的角度, 所以 AC 是最长的一面。 下一个角度是 67 , BC 是下一个最长的一面 。 27 是最小的一面, AB 是最短的一面 。 答案是 AB, BC, AC 。

  播放段落

  Example 4
  ::例4

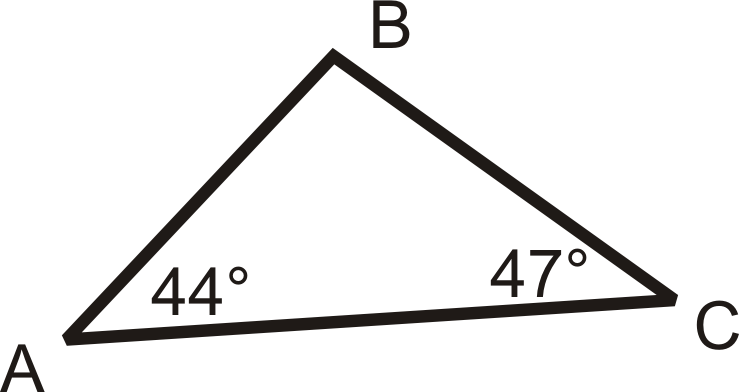
  播放段落

  List the angles in order, from largest to smallest.
  ::列出按顺序排列的角度,从最大角度到最小角度。

  

  播放段落

  Just like with the sides, the largest angle is opposite the longest side. The longest side is $\begin{align*}BC\end{align*}$ , so the largest angle is $\begin{align*}\angle A\end{align*}$ . Next would be $\begin{align*}\angle B\end{align*}$ and then $\begin{align*}\angle C\end{align*}$ .
  ::就像侧边一样,最大的角度是相对最长的一边。 最长的一边是 BC, 所以最大的角度是 QA。 下一个是 QB, 然后是 QC 。

  播放段落

  Example 5
  ::例5

  播放段落

  List the sides in order, from least to greatest.
  ::按顺序列出双方名单,从最少到最多。

  

  播放段落

  To solve, let’s start with $\begin{align*}\triangle DCE\end{align*}$ . The missing angle is $\begin{align*}55^\circ\end{align*}$ . By the theorem presented in this section, the sides, in order from least to greatest are $\begin{align*}CE, \ CD\end{align*}$ , and $\begin{align*}DE\end{align*}$ .
  ::解决之道,让我们从“DCE ” ( DCE ) 开始。 缺失的角度是 55 。 根据本节的理论,从最小到最大,两边是 CE 、 CD 和 DE 。

  播放段落

  For $\begin{align*}\triangle BCD\end{align*}$ , the missing angle is $\begin{align*}43^\circ\end{align*}$ . Again, by the theorem presented in this section, the order of the sides from least to greatest is $\begin{align*}BD, \ CD\end{align*}$ , and $\begin{align*}BC\end{align*}$ .
  ::对于 {BCD } 来说, 缺失的角度是 43\\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ BCD \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

  播放段落

  By the SAS Inequality Theorem, we know that $\begin{align*}BC > DE\end{align*}$ , so the order of all the sides would be: $\begin{align*}BD, \ CE, \ CD, \ DE, \ BC\end{align*}$ .
  ::根据SAS不平等理论,我们知道BC>DE, 所以各方的顺序是:BD、CE、CD、DE、BC。

  播放段落

  Review
  ::回顾

  播放段落

  For questions 1-3, list the sides in order from shortest to longest.
  ::问题1-3,按从最短到最长顺序列出两边。

  1. 
  2. 
  3. 

  播放段落

  For questions 4-6, list the angles from largest to smallest.
  ::对于问题4-6,请列出从最大角度到最小角度。

  4. 
  5. 
  6. 
  播放段落
  7. Draw a triangle with sides 3 cm, 4 cm, and 5 cm. The angle measures are approximately $\begin{align*}90^\circ, \ 53^\circ\end{align*}$ , and $\begin{align*}37^\circ\end{align*}$ . Place the angle measures in the appropriate spots.
     ::绘制边有 3 cm, 4 cm, 5 cm 5 cm 的三角形。 角度量度约为 90 , 53 , 37 。 将角量度放在适当的点上 。
  播放段落
  8. Draw a triangle with angle measures $\begin{align*}56^\circ, \ 54^\circ\end{align*}$ and the included side is 8 cm. What is the longest side of this triangle?
     ::绘制角度为 56 , 54 和包含边为 8 cm 的三角形。 此三角形最长的一面是什么 ?
  播放段落
  9. Draw a triangle with sides 6 cm, 7 cm, and 8 cm. The angle measures are approximately $\begin{align*}75.5^\circ, \ 58^\circ\end{align*}$ , and $\begin{align*}46.5^\circ\end{align*}$ . Place the angle measures in the appropriate spots.
     ::绘制边6厘米、 7厘米和 8厘米的三角形。 角度量度约为 75.5 、 58 和 46.5 。 将角量度放在适当的点上 。
  播放段落
  10. What conclusions can you draw about $\begin{align*}x\end{align*}$ ?
      ::您能得出x的什么结论?
  播放段落
  11. Compare $\begin{align*}m \angle 1\end{align*}$ and $\begin{align*}m \angle 2\end{align*}$ .
      ::比较 m1 和 m2。
  播放段落
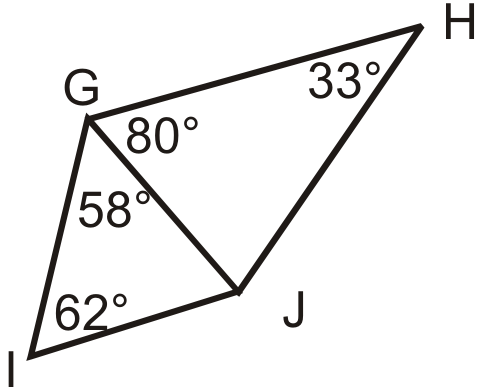
  12. List the sides from shortest to longest.
      ::列出从最短到最长的两边。
  播放段落
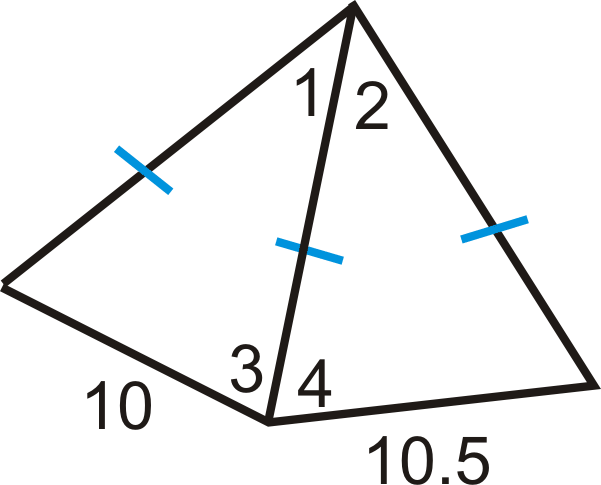
  13. Compare $\begin{align*}m \angle 1\end{align*}$ and $\begin{align*}m \angle 2\end{align*}$ . What can you say about $\begin{align*}m \angle 3\end{align*}$ and $\begin{align*}m \angle 4\end{align*}$ ?
      ::比较m*1和m*2,你能说什么 关于m*3和m*4?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源